傅里叶级数展开的求解方法

傅里叶级数展开的求解方法

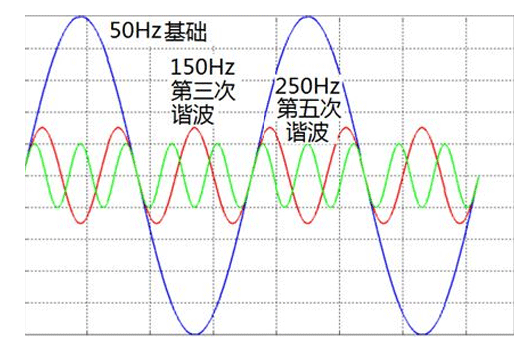
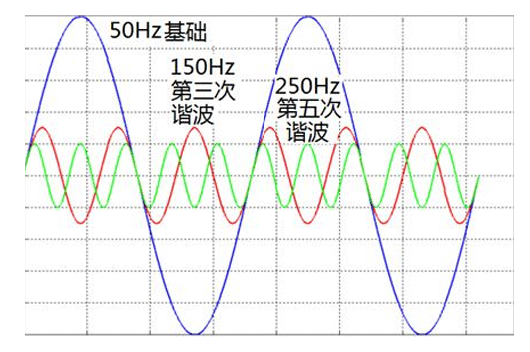
傅里叶级数展开是一种将周期函数分解为一系列正弦或余弦函数的方法。该方法在数学、物理、信号处理、图像处理和工程等领域中得到广泛应用。本文将探讨傅里叶级数展开的定义、求解方法以及应用等方面。

1. 傅里叶级数展开的定义

在一个周期为T的函数f(x)中，其傅里叶级数可以表示为：

$$ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos(2n\pi x/T)+b_n\sin(2n\pi x/T)) $$

其中，a0、an、bn均为常数，n为正整数。a0是函数f(x)在一个周期内的平均值，an和bn分别是f(x)在一个周期内的正弦和余弦函数的振幅，且f(x)的振幅趋近于0。

2. 傅里叶级数展开的求解方法

傅里叶级数展开的求解方法主要有复合公式和欧拉公式两种方法。

（1）复合公式法

复合公式法是通过求解傅里叶系数an和bn的积分来得到傅里叶级数展开的，其公式为：

$$ a_n=\frac{2}{T}\int_0^T{f(x)\cos(2n\pi x/T)}dx $$

$$ b_n=\frac{2}{T}\int_0^T{f(x)\sin(2n\pi x/T)}dx $$

其中，an和bn均为常数，n为正整数。

该方法的缺点是需要对f(x)进行多次积分，计算量大且耗时较长。因此，在实际计算中并不常用。

（2）欧拉公式法

欧拉公式法是通过将周期函数f(x)分别表示为cos(x)和sin(x)的级数，再根据其正弦和余弦函数分别进行傅里叶级数展开的方法。其公式为：

$$ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos(n\omega x)+b_n\sin(n\omega x)) $$

其中，ω=2π/T。f(x)的傅里叶系数可以表示为：

$$ a_0=\frac{2}{T}\int_0^T{f(x)}dx $$

$$ a_n=\frac{2}{T}\int_0^T{f(x)\cos(n\omega x)}dx\quad $$
$$ b_n=\frac{2}{T}\int_0^T{f(x)\sin(n\omega x)}dx $$

该方法的优点是计算简单、易于理解并且较为常用。在实际计算中，常用欧拉公式法进行傅里叶级数展开的求解。

3. 傅里叶级数展开的应用

傅里叶级数展开有着广泛的应用，主要包括以下几个方面：

（1）信号处理

在信号处理中，可将信号分解为傅里叶级数，通过对信号频域信息的分析得出有关信号特征的信息。例如，计算傅里叶系数的幅频响应，可以得到信号的主要频率成分，进而对信号的特定部分进行滤波操作。

（2）图像处理

在图像处理中，可对图像进行傅里叶级数展开，分析图像的频域信息并进行滤波处理，以达到去噪、锐化、平滑等效果。

（3）电子工程

在电子工程中，傅里叶级数展开可以用于计算电路的频率响应特性、滤波器的传递函数等。

（4）物理学

在物理学中，傅里叶级数展开可以用于计算周期性物理量的谐振频率、衰减时间等参数，以及对物理现象的频域特征进行研究。

4. 总结

本文详细介绍了傅里叶级数展开的定义、求解方法以及应用。其中，欧拉公式法是较为常用的求解方法，而傅里叶级数展开在信号处理、图像处理、电子工程、物理学等领域中有着广泛的应用。傅里叶级数不仅有着极高的理论价值，同时也在实际应用中发挥着重要的作用。