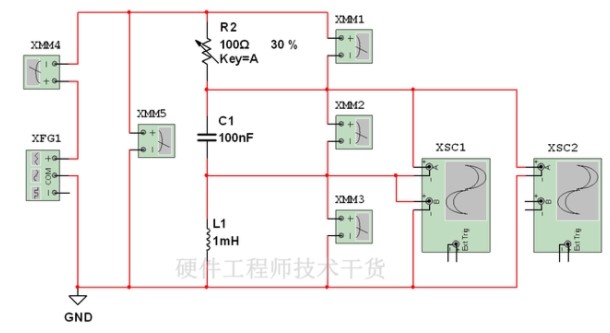
仿真一下串联谐振电路,如下:
1、XMM1、XMM2、XMM3,XMM5测量交流电压
2、XMM4测量交流电流
3、XFG1信号发生器,输出正弦波,频率赋值都可调
4、XSC1两个通道分别测量电容和电感两端波形
5、XSC2测量电容和电感串联后两端波形
谐振频率计算公式如下:

1、电路参数:
L1= 1mH
C1= 100nF
R2 = 可调电阻调整到30R
2、首先观察谐振状态现象:
根据以上公式计算此电路谐振频率f=15924Hz。配置信号发生器为正弦波,频率15924Hz,振幅为2V,也就是输出有效值是1.414V。仿真数据如下:
1)电阻两端电压为1.408V接近1.414V输出电压,也就是LC两端的总电压几乎为0,电路呈现纯电阻特性。
2)电流约47mA。
3)电容和电感两端电压几乎相等,4.7V左右,这里是交流有效值,比信号发生器输出高出不少。

4)L和C两端波形,大小相等相位相反,见下面仿真波形。

LC串联后两端波形,峰峰值不到400mV,有效值约0.14V很小。

3、调整R2电阻观察现象:
1)R2调整到10欧姆,基本还是在谐振状态,L和C两端电压明显增大,电流也增大。

2)R2调整到50欧姆,基本还是在谐振状态,L和C两端电压明显减小,电流也减小。

由此可见调整R2电阻能够明显改变L和C的电压,基本不会影响谐振状态。为什么会出现这种状态呢?因为理想状态下,谐振状态时电路呈现纯电阻特性,电路电流取决于R2,R2两端的电压就是信号发生器输出电压,R2减小电流增大,因为频率、容值、感值都没有变化,所以L和C的感抗和容抗没有变化,电流增大后,L和C两端电压也增大。R2增加同理。L和C阻抗计算公式如下:
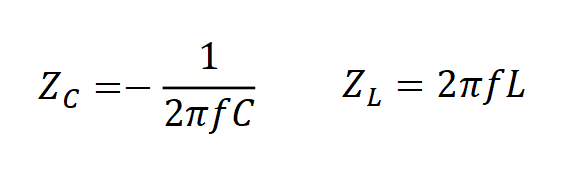
4、尝试更改频率,观察现象。
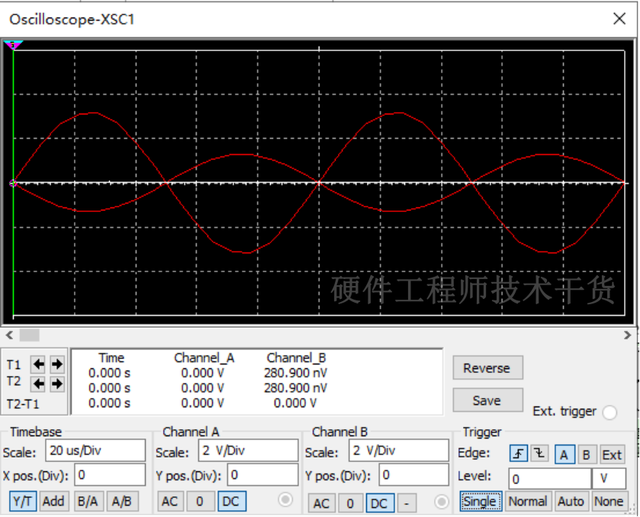
1)调整输出频率为10KHz,频率减小后容抗增大,感抗减小,电路呈现容性,L和C波形如下,电容的幅值大。
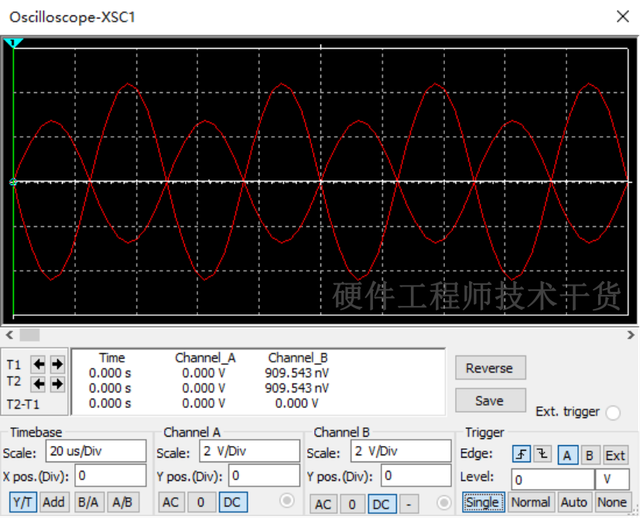
2)调整输出频率为20KHz,频率增大后容抗减小,感抗增大,电路呈现感性,L和C波形如下,电感幅值大。
5、串联谐振总结
和非谐振状态相比,谐振状态阻抗是最小的,电流是最大的,电路呈现纯电阻特性,电流和电压同相位,电感和电容两端可能出现比输入电压高很多倍的电压,因此串联谐振又称为电压谐振。
-
电容器
+关注
关注
64文章
6222浏览量
99686 -
电感器
+关注
关注
20文章
2331浏览量
70544 -
谐振电路
+关注
关注
11文章
165浏览量
26972 -
信号发生器
+关注
关注
28文章
1474浏览量
108772 -
RLC串联电路
+关注
关注
1文章
18浏览量
8451
发布评论请先 登录
相关推荐




 RLC串联谐振电路仿真分析
RLC串联谐振电路仿真分析











评论