电机运动控制算法之S速度曲线规划算法

转自| 小麦大叔

搞过电机或运动控制的小伙伴应该知道，S曲线很重要，下面一张动图对比一下，你就知道S曲线的好处。

今天就给大家描述一下S速度曲线规划算法。

1 前言

S形加减速的最重要特征是该算法的加速度/减速度曲线的形状如字母 S。S形加减速的速度曲线平滑 ,从而能够减少对控制过程中的冲击，并使插补过程具有柔性 [^1]。由于T形曲线在加速到匀速的切换过程中，实际中存在较大过冲，因此这里对比一下T曲线和7段S曲线的实际过程；

T形：加速 -> 匀速 -> 减速

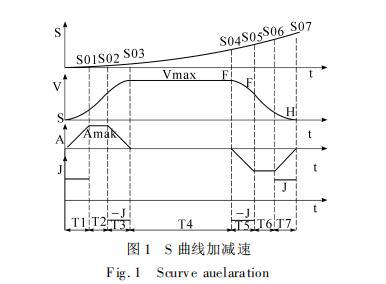
S形：加加速(T1) -> 匀加速(T2) -> 减加速(T3)-> 匀速(T4)-> 加减速(T5)-> 匀减速(T6)-> 减减速(T7)

上文在加速这块的文字描述可能读起来起来有点绕，下面看图：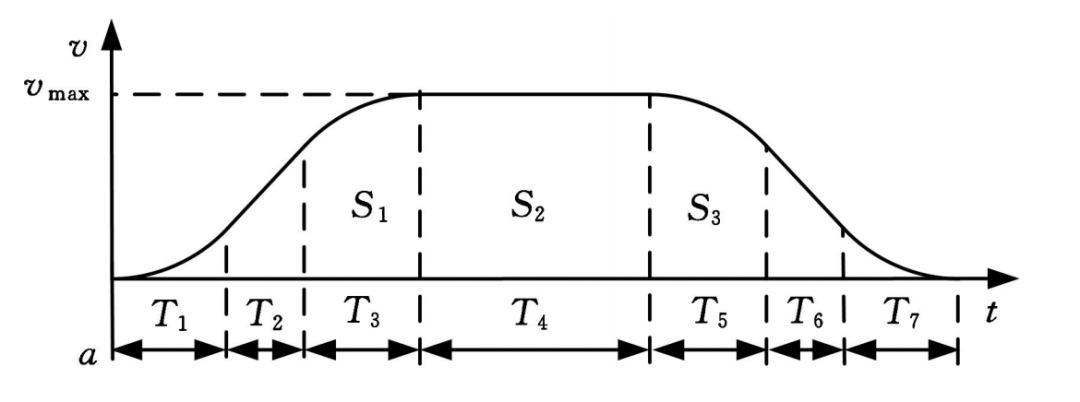

2 理论分析

由于S曲线在加减速的过程中，其加速度是变化的，因此这里引入了新的一个变量 J，即加加速度。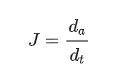

因此对应上图的7段S速度曲线中，规定最大加速为amax，最小加速度为-amax，则加速度的关系；

所以通常需要确定三个最基本的系统参数 :系统最大速度umax ，最大加速度a_{max} ，加加速度，就可以可确定整个运行过程[^2] ；

最大速度：反映了系统的最大运行能力 ；

最大加速度：反映了系统的最大加减速能力 ；

加加速度：反映了系统的柔性；

柔性越大，过冲越大，运行时间越短；

柔性越小，过冲越小，运行时间越长；

2.1 加速度时间关系方程

整个加速度变化的过程具体如下图所示；

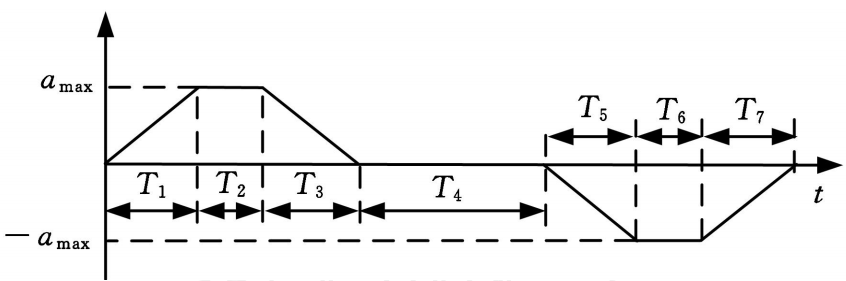
2.2 速度时间关系方程

速度和加速度满足 ；加加速度和速度的关系满足：

结合加速度时间关系并结合② 式可以得到速度曲线关系，具体关系如下图所示；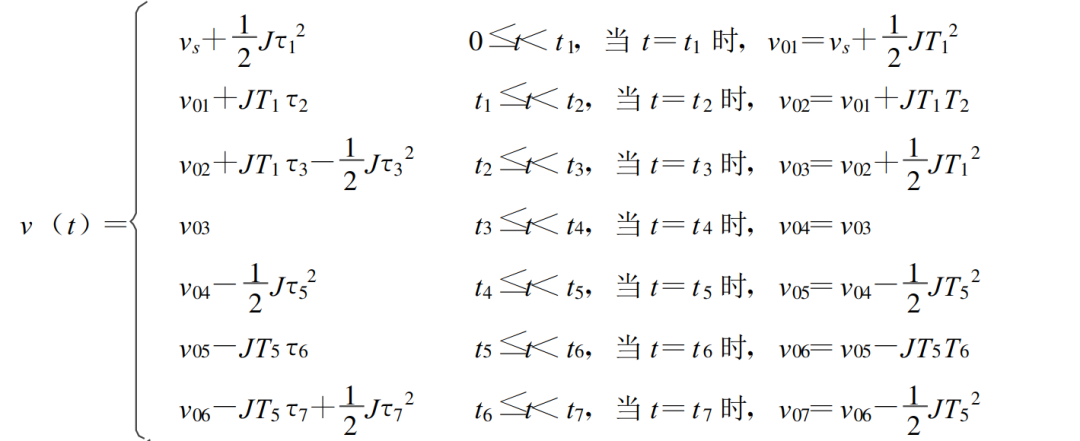

进一步简化可以得到：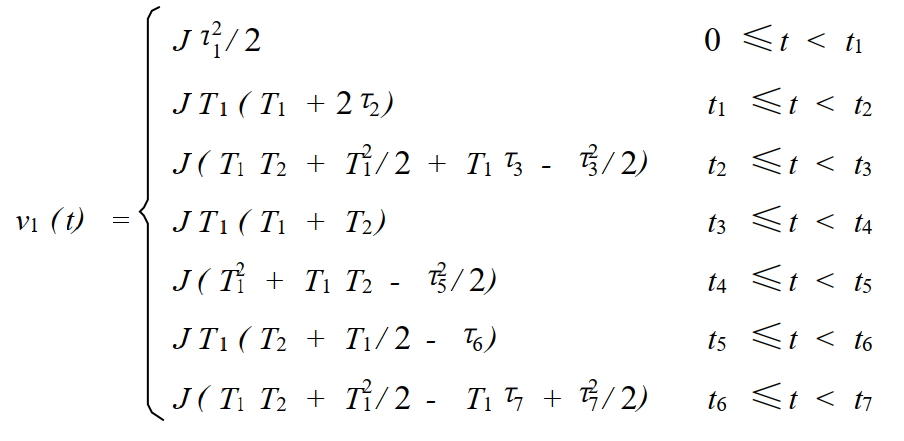

2.3 位移时间关系方程

积分忘的差不多了，回去再复习一下；

最终位移的方程如下所示；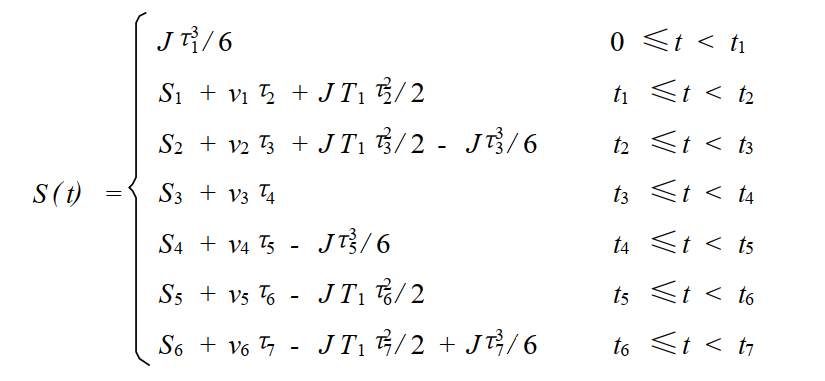

3 程序实现的思路

正如前面所提到的，S曲线规划需要确定三个最基本的系统参数 ：系统最大速度 ，最大加速度a_{max} ，加加速度，这样就可以确定这个运行过程。这里有一个隐性的条件，就是在运行的过程中可以达到最大速度，这样才是完整的7段S曲线，另外这里还有一些中间参数：

4 matlab 程序

matlab程序亲测可以运行，做了简单的修改，因为这里直接给定了整个运行过程的时间，所以需要在SCurvePara函数中求出加加速度 的值，路程为 1：

SCurvePara

function[Tf1,V,A,J,T]=SCurvePara(Tf,v,a)
T=zeros(1,7);
fori=1:1000
%加加速度J
J=(a^2*v)/(Tf*v*a-v^2-a);
%Tk
T(1)=a/J;
T(2)=v/a-a/J;%t2=v/a-t1;
T(3)=T(1);
T(4)=Tf-2*a/J-2*v/a;%t4=Tf-4*t1-2*t2;
T(5)=T(3);
T(6)=T(2);
T(7)=T(1);
%根据T2和T4判断S曲线的类型
ifT(2)< -1e-6
        a = sqrt(v*J);
        display('t2<0');
    elseif T(4) < -1e-6
        v = Tf*a/2 - a*a/J;
        display('t4<0');
    elseif J < -1e-6
        Tf = (v^2 + a) / (v*a) + 1e-1;
        display('J<0');
    else
        break;
    end
end

 A = a;
 V = v;
 Tf1 = Tf;
 end

SCurveScaling

functions=SCurveScaling(t,V,A,J,T,Tf)
%J=(A^2*V)/(Tf*V*A-V^2-A);
%T(1)=A/J;
%T(2)=V/A-A/J;%T(2)=V/A-T(1);
%T(3)=T(1);
%T(4)=Tf-2*A/J-2*V/A;%T(4)=Tf-4*T(1)-2*T(2);
%T(5)=T(3);
%T(6)=T(2);
%T(7)=T(1);
%%
if(t>=0&&t<= T(1))
    s = 1/6 * J * t^3;
elseif (  t >T(1)&&t<= T(1)+T(2) )
    dt = t - T(1);
    s = 1/2 * A * dt^2 + A^2/(2*J) * dt...
        + A^3/(6*J^2);
elseif ( t >T(1)+T(2)&&t<= T(1)+T(2)+T(3) )
     dt = t - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t >T(1)+T(2)+T(3)&&t<= T(1)+T(2)+T(3)+T(4) )
     dt = t - T(1) - T(2) - T(3);
     s = V*dt ...
         +  (-1/6*J*T(3)^3) + 1/2*A*T(3)^2 + (A*T(2) + A^2/(2*J))*T(3) + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t >T(1)+T(2)+T(3)+T(4)&&t<= T(1)+T(2)+T(3)+T(4)+T(5) )
     t_temp = Tf - t; 
     dt = t_temp - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
     s = 1 - s;
elseif ( t >T(1)+T(2)+T(3)+T(4)+T(5)&&t<= T(1)+T(2)+T(3)+T(4)+T(5)+T(6) )
     t_temp = Tf - t; 
     dt = t_temp - T(1);
     s = 1/2 * A * dt^2 + A^2/(2*J) * dt + A^3/(6*J^2);
     s = 1 - s;  
elseif ( t >T(1)+T(2)+T(3)+T(4)+T(5)+T(6)&&t<= T(1)+T(2)+T(3)+T(4)+T(5)+T(6)+T(7) + 1e5 )
     t_temp = Tf - t; 
     s = 1/6 * J * t_temp^3;
     s = 1 - s;     
end
 
end

测试的代码如下：TEST

%%
N=500;

ThetaStart=0;%起始位置
ThetaEnd=90;%最终位置
VTheta=90;%1速度
ATheta=135;%1.5加速度
Tf=1.8;%总行程时间

v=VTheta/(ThetaEnd-ThetaStart);
a=ATheta/(ThetaEnd-ThetaStart);
v=abs(v);
a=abs(a);


Theta=zeros(1,N);
s=zeros(1,N);
sd=zeros(1,N);
sdd=zeros(1,N);

[TF,V,A,J,T]=SCurvePara(Tf,v,a);
display(J,'J:');
display(TF,'Tf:');
display(V,'v:');
display(A,'da:');

display(TF-Tf,'dTf:');
display(V-v,'dv:');
display(A-a,'da:');

t=linspace(0,TF,N);
dt=t(2)-t(1);
fori=1:N
ifi==N
a=a;
end
s(i)=SCurveScaling(t(i),V,A,J,T,TF);
Theta(i)=ThetaStart+s(i)*(ThetaEnd-ThetaStart);
ifi>1
sd(i-1)=(s(i)-s(i-1))/dt;
end
ifi>2
sdd(i-2)=(sd(i-1)-sd(i-2))/dt;
end
end

subplot(3,1,1);
legend('Theta');
xlabel('t');
subplot(3,1,1);
plot(t,s)
legend('位移');
xlabel('t');
title('位置曲线');

subplot(3,1,2);
plot(t,sd);
legend('速度');
xlabel('t');
title('速度曲线');

subplot(3,1,3);
plot(t,sdd);
legend('加速度');
xlabel('t');
title('加速度曲线');

看到最终仿真结果和预期相同；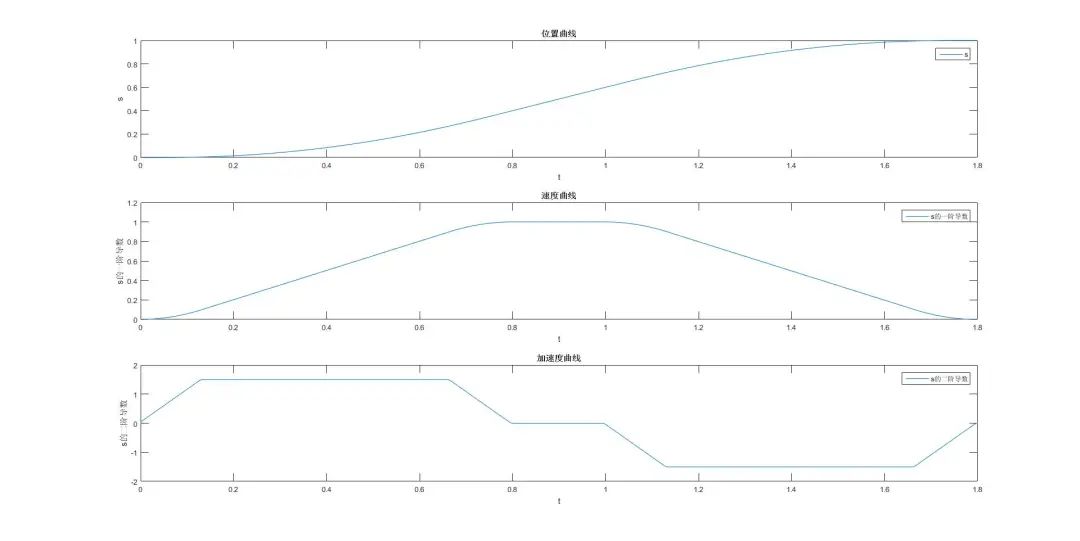

最后再看一下T形和S形速度曲线规划的效果对比：

5 总结

本文只对7段的S曲线规划做了详细的推导和介绍，matlab中的程序对于4段和5段都有做实现，很多是在理想情况下进行推导的，初始速度默认为0，终止速度也为0，并且假设加减速区域相互对称。最终运行结果符合预期效果。

审核编辑：汤梓红