理论分析
傅里叶变换中提到:任意波形均可分解为无数不同幅值和频率的正弦波的叠加。那么以最常见的方波(在工作中是以时钟信号,PWM信号等等出现)为分析对象,幅值为1,频率为1/T的方波波形,如下图所示:
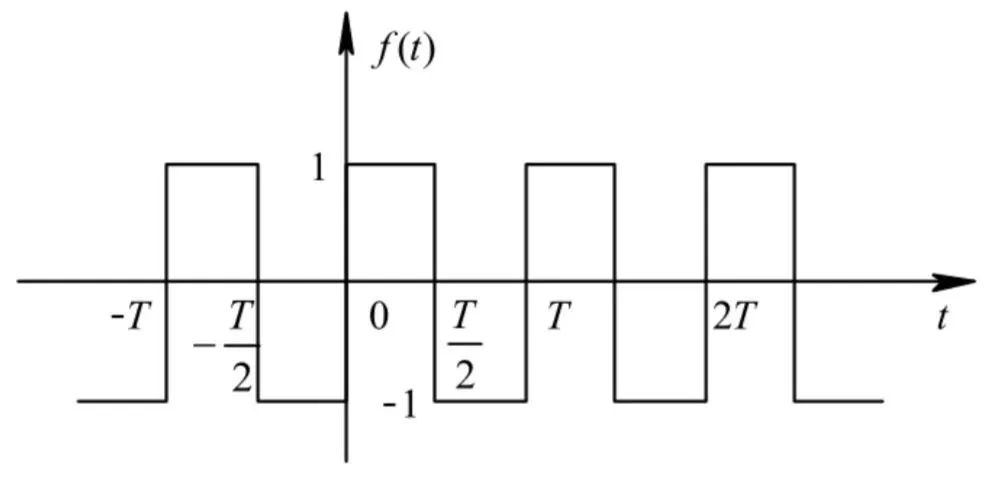
通过傅里叶变换后,方波公式可以列为:
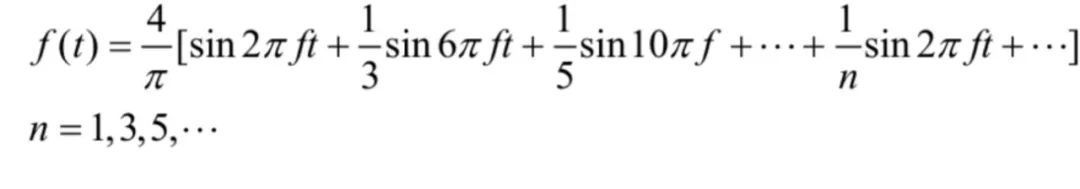
上式的意思是:
方波可以分解为频率为 f 赫兹(f=1/T)幅值为
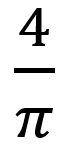
的正弦波,加上频率为 3*f 幅值为
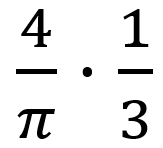
的正弦波,再加上频率为5*f幅值为
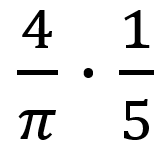
的正弦波,以此类推无数正弦波的叠加。
仿真验证
那么就开始做一下仿真验证一下,首先用PSpice输出一个频率为1kHz,幅值为1V的方波。时域波形如下所示:
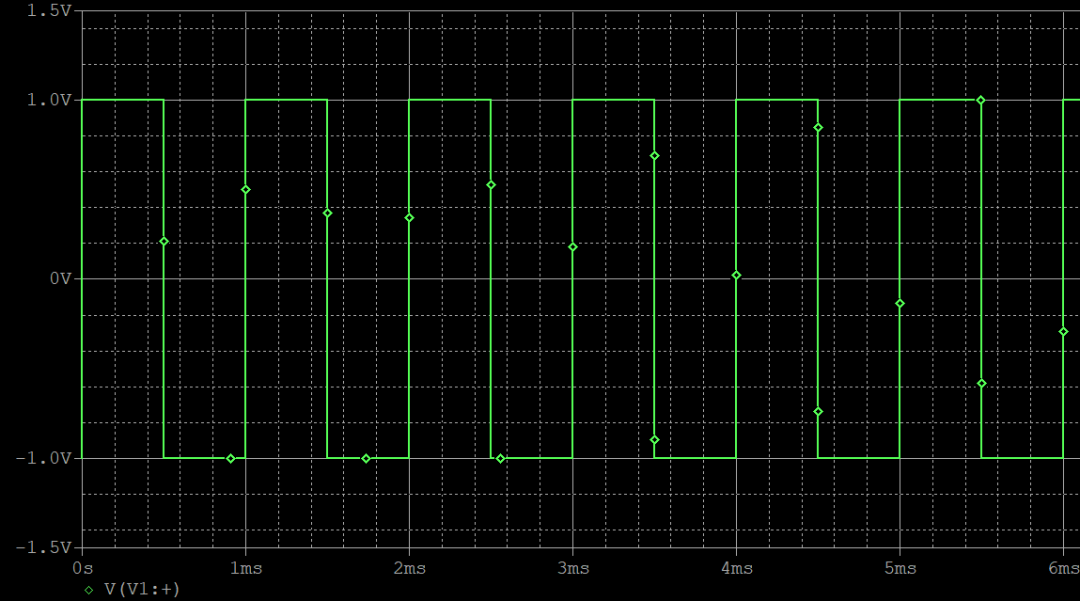
对波形进行傅里叶变换后,转化为频域,波形如下图所示:
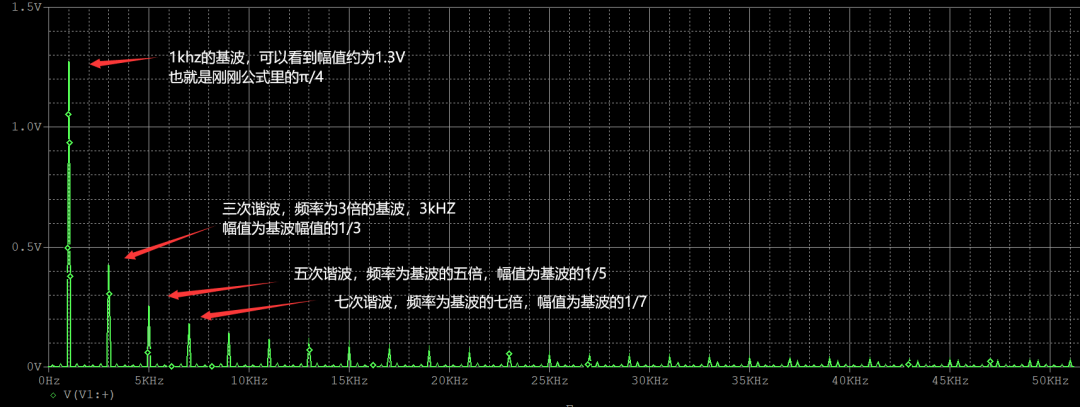
从频域图中,可以发现,基波频率和方波频率相同,基波的幅值为方波幅值的
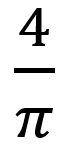
倍,这些也均和之前得到的公式中分析的一样,X次谐波频率为基波的X倍,幅值为基波的1/X;谐波的幅值会随谐波频率的增加而减小。
那么频域的分解我们得到了,是不是可以反推回去呢?这个我就直接找了一个multisim的仿真图(书内带的仿真,回复:模拟电子技术基础,获得书以及配套书的所有仿真,方便理解强烈推荐!!),图为通过反相加法器,将不同频率的正弦波叠加到一起(不同频率有不同权重,三次谐波放大倍数为
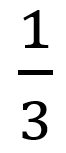
,五次谐波放大倍数为
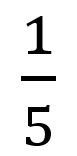
,以此类推)。正弦波1kHZ基波幅值设置
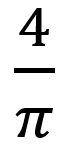
V,约等于1.2732V。那么只看基波的波形是这样的:
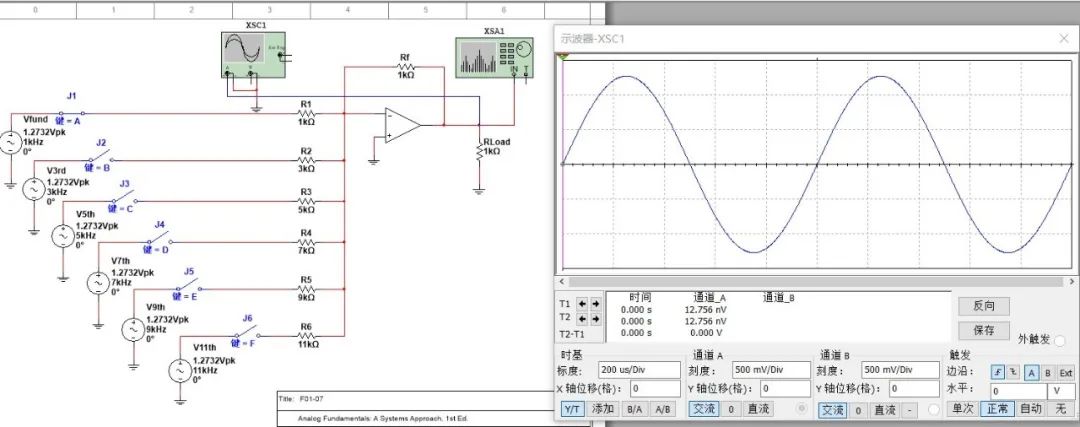
基波+三次谐波:
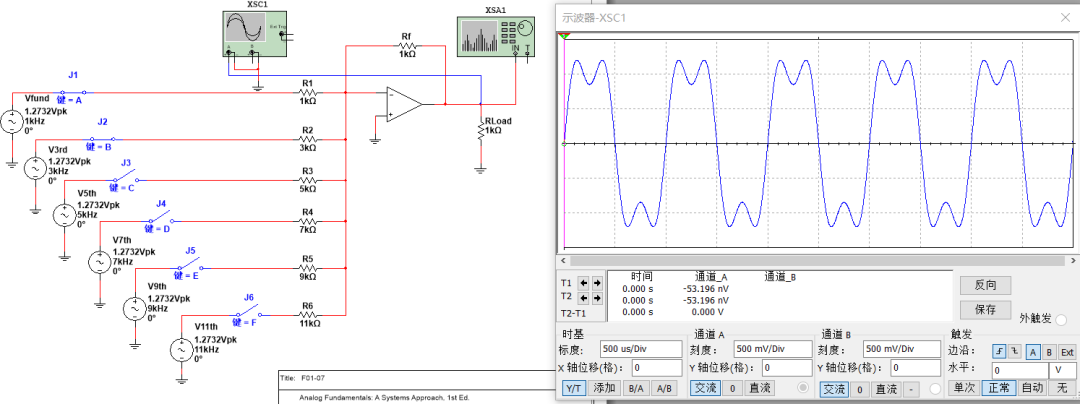
基波+三次谐波+五次谐波,是不是已经看到方波的样子了:
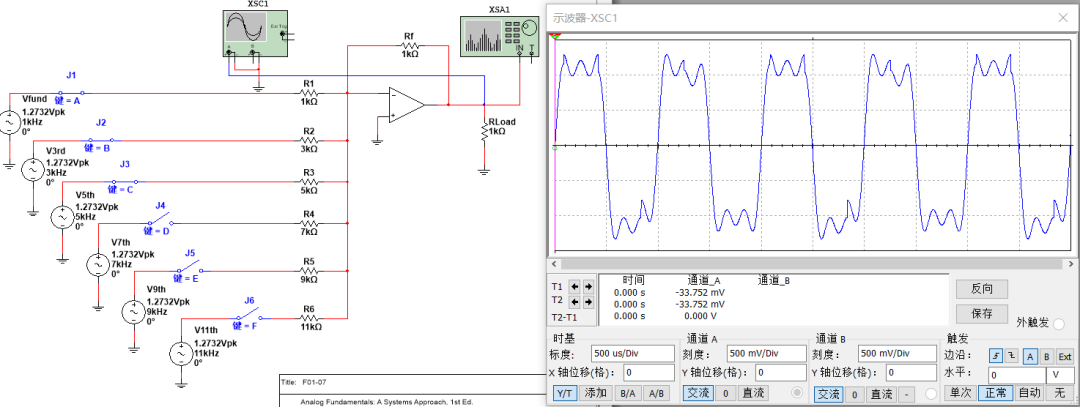
基波+三次谐波+五次谐波+七次谐波,是不是更像方波了:
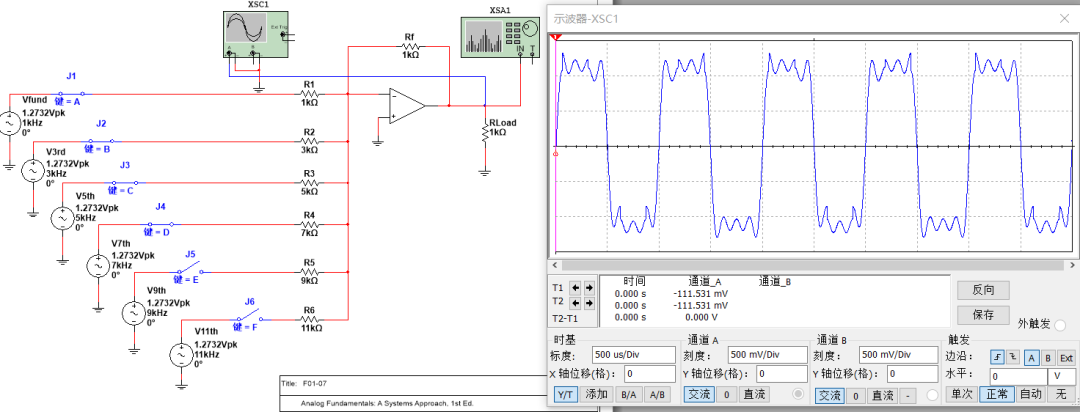
基波+三次谐波+五次谐波+七次谐波+九次谐波+十一次谐波:
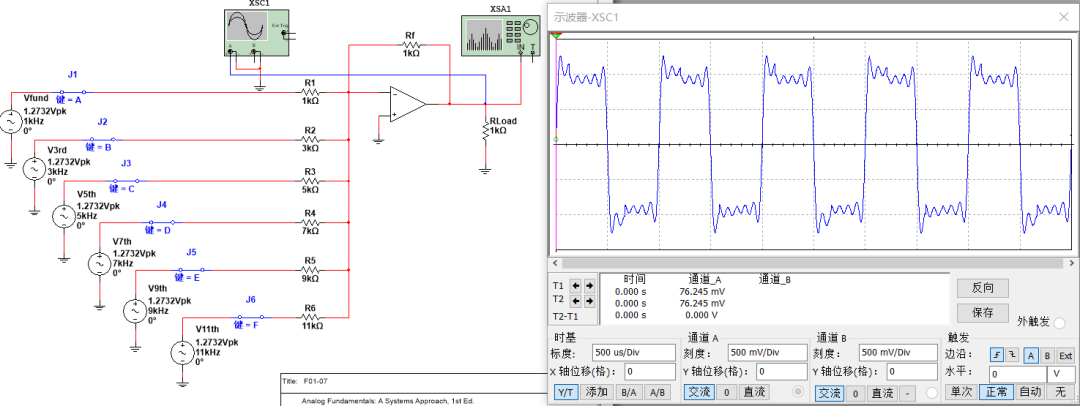
由于篇幅的关系,只叠加到了十一次谐波,不过看幅值已经很接近幅值为1V频率为1kHz的方波了!!
不过这时,不知您是否心中会闪过一丝疑问:为什么只有奇次谐波,没有看到偶次谐波??那么在这里只提一个结论,推导过程就不列在本文了。
结论是:占空比为50%的方波没有偶次谐波。只有占空比不是50%的方波才有偶次谐波。(所以大多数可以看到的谐波是奇次谐波)
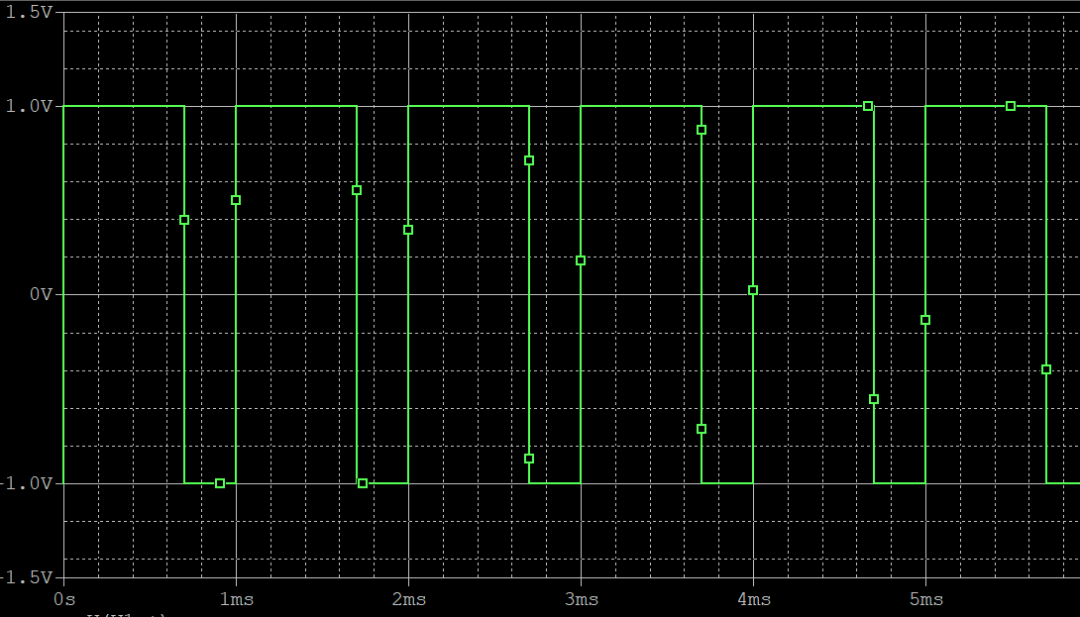
那么就继续用PSpice验证这一结论,在原来波形的基础上将占空比从50%修改到70%,1kHz频率和1V幅值保持不变。时域波形如下所示:
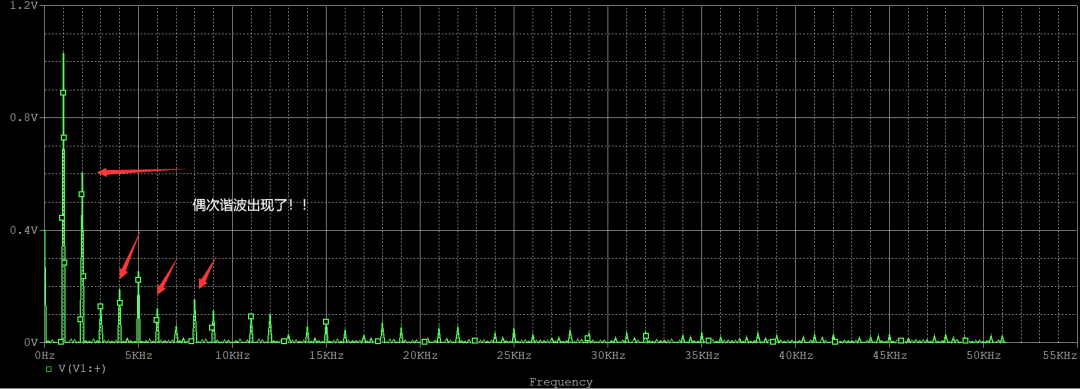
对其进行傅里叶变换,转化到频域,波形如下,偶次谐波出现了!!
最后说两句
那么读到这里,是不是您的心里是不是已经明白示波器的带宽为什么这么重要了呢?如果您的示波器带宽太小,或者您在测量高速信号(比如10Mhz或者更高)的时候无意间打开了带宽限制,那么方波的高次谐波就被滤掉啦哈哈。
所以您观察到的方波就变形了,就失真了,就像用multisim仿真的那个只叠加到十一次谐波的方波一样,出现了失真!!
同理可推运算放大器的带宽(要放大方波信号的时候要考虑其高次谐波,不能仅仅只看基波的频率)。
-
PWM
+关注
关注
114文章
5209浏览量
215690 -
信号
+关注
关注
11文章
2819浏览量
77342 -
仿真验证
+关注
关注
0文章
25浏览量
8172 -
傅里叶变换
+关注
关注
6文章
442浏览量
42784
发布评论请先 登录
相关推荐
第23章 傅里叶变换
快速傅里叶变换C语言实现
DSP变换运算-傅里叶变换
小波变换比傅里叶变换好在哪里_小波变换与傅里叶变换详解





 傅里叶变换的理论分析和仿真验证
傅里叶变换的理论分析和仿真验证










评论