大多数电子工程师都非常熟悉波特图。我们使用这个术语指的是图,其中水平轴表示对数频率,垂直轴表示量级(以分贝表示)或相位。最初的波特图是系统实际频率响应的直线近似值,但是现在我们也使用该术语来表示由仿真软件生成的数学精确图。然而,存在另一种直观描述系统响应不同输入频率的方法。它被称为奈奎斯特图(或奈奎斯特图),主要用于稳定性分析。In可能不如波特图更直观,但它更直接地表明放大器是否稳定,并且它可以同时传达振幅和相位信息。
极坐标图与笛卡尔图
奈奎斯特图是极坐标图,我认为我们应该通过简要回顾极坐标的概念来开始讨论。最常见的图形类型具有沿水平轴增加的独立变量和通过改变垂直位置表示的因变量。我们使用“笛卡尔”这个词来识别这个系统,它通过两个轴的水平和垂直距离传达信息。
另一方面,极坐标图通过指示幅度和角度来传达信息。大小对应于从原点到曲线上的任何点的径向距离,并且角度是从正水平轴逆时针测量的。在下图中,幅度用r表示,角度用θ表示。
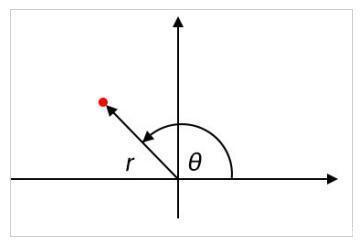
复数
由于极坐标图本质上与由大小和角度组成的有序对的概念有关,所以当我们处理复数时它们特别有用。用极性形式表示的复数可以直接转换成极性图的大小和角度,也可以用矩形形式将虚部指定给纵轴,实部指定给横轴来定位点。
奈奎斯特图
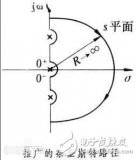
波特图传达幅度或相位与频率的关系。因此,你需要两个图来描述系统的幅度和相位响应(或者至少需要两条波特曲线,你可以将两条曲线合并到同一图中)。另一方面,在奈奎斯特图中,只需要一条曲线。这是可能的,因为奈奎斯特图是极性的:曲线上的每个点都表示幅度(通过距离原点的距离)和相位(通过几何角度),形成曲线的众多不同点反映了系统对众多不同输入频率的响应。奈奎斯特图中的频率从0延伸到无穷大,箭头用于指示频率增加的方向。在我们考虑一个例子后,我认为这将更加清晰。下图是一阶RC低通滤波器的奈奎斯特图。

详细研究这个图,以确保理解正在看的东西。
奈奎斯特绘图示例
问:首先,为什么有两条曲线?
答:实线表示正频率,虚线表示负频率。它们是彼此的镜像,忽略虚线。
问:频率信息在哪里?
答:记住,曲线从ω= 0延伸到ω=∞,箭头表示频率增加的方向。因此,实线曲线在曲线右侧的ω= 0处开始(在实轴上的值为1)并且在原点处结束,其对应于ω=∞。
问:如何解释半圆形幅度响应?
答:我们已经熟悉RC低通滤波器的行为,所以让我们用我们所知的来解开这个奈奎斯特图。在曲线开始的点处(即在ω= 0处),与原点的距离为1。换句话说,低频增益是统一的。随着频率的增加,从原点到曲线的径向距离再次减小,这正是我们所期望的,因为较短的径向距离对应于更多的衰减。在曲线结束的点(即ω=∞),从原点到曲线的距离为零,因为当频率达到无穷大时,低通滤波器产生无限衰减。
问:可以看到角度如何从0°开始,如预期的那样,但是低通滤波器应该具有-90°的最终相移。如何在奈奎斯特图中反映出来?我无法测量直接位于原点顶部的点的相位。
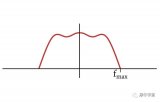
答:这有点令人困惑,但是如果你关注曲线接近原点时的行为,你可以看到角度倾向于-90°。这在下图中描述,这也是我们到目前为止所学到的内容的总结。
结论
我希望你现在能够清楚地了解奈奎斯特图的最基本特征。
-
放大器
+关注
关注
143文章
13604浏览量
213597 -
衰减器
+关注
关注
4文章
640浏览量
34363 -
波特图
+关注
关注
1文章
29浏览量
11322 -
RC低通滤波器
+关注
关注
0文章
13浏览量
8587
发布评论请先 登录
相关推荐
DAC的高次谐波为什么都会折叠回第一奈奎斯特区间?
超越第一奈奎斯特区域,将那奎斯特混叠变为优势
奈奎斯特采样定理
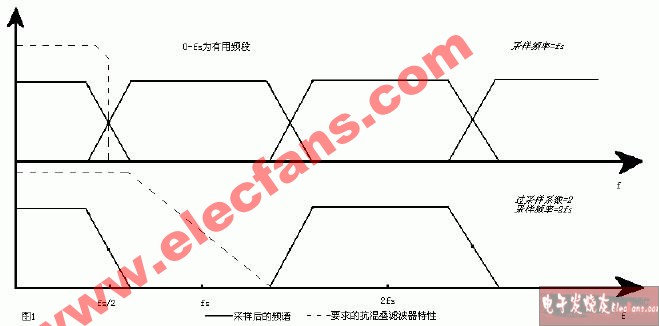
将直接转换推向奈奎斯特带宽的设计以及和中频采样进行比较




 怎样使用奈奎斯特图进行交流电分析呢?
怎样使用奈奎斯特图进行交流电分析呢?











评论