评论:二阶过滤器
当我说“二阶”滤波器时,我指的是使用电感 - 电容(LC)谐振或放大器的滤波器,以产生真正的二阶传递函数。您可以通过级联两个一阶无源滤波器来实现两极频率响应,但是得到的电路没有复共轭极点,因此传输函数无法优化,因为Q因子始终为0.5。相比之下,设计人员可以控制基于谐振或放大器的二阶滤波器的Q因子,使其有利于平坦通带,线性相位响应或快速通带到阻带转换。
本文中的信息一般适用于二阶滤波器,但在我撰写本文时,我想到的电路是下面显示的RLC二阶低通滤波器。
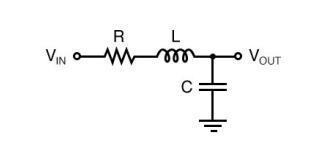
该滤波器的截止频率由电容器和电感器的值决定,Q因子可以通过改变电阻器的值来改变。当你与Nyquist图的工作,需要记住的是截止频率(很重要的ω 二阶滤波器)是不是一定-3dB频率。在增益ω 可以是-3分贝,比-3 dB的降低,或小于-3分贝根据过滤器的Q因子大。
奈奎斯特图中的象限
您可能会注意到关于二阶奈奎斯特图的第一件事是它延伸到复平面的左下象限。例如:
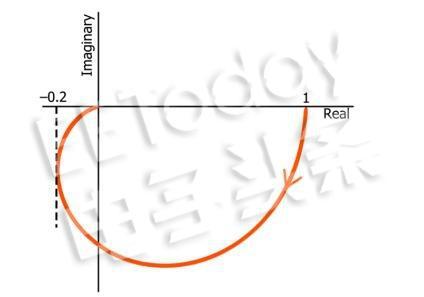
请注意,本文中显示的所有图都不包含负频率。
由于曲线延伸到左下象限但不进入左上象限,我们立即知道它代表二阶滤波器。为什么?那么,负虚轴对应于-90°的相移,如果奈奎斯特迹线穿过该轴并延伸到左下象限,则滤波器必须具有多个极点,因为您只能获得-90°的相位每极移位。它不能有三个极点,因为角度不会超过-180°(对应于负实轴)。你可以看到曲线在接近原点时倾向于-180°,正如随着频率向无穷大增加,两极滤波器的相移渐近接近-180°。
二阶滤波器的截止频率
与一阶奈奎斯特图一样,二阶滤波器的奈奎斯特图不会给出截止频率。然而,与一阶情况相比,我们无法通过在曲线上寻找幅度响应为1/√2的点来找到一般的截止频率位置。这是因为(如上所述)在增益ω 由电路的Q因子的影响。然而,无论Q如何,相移在截止频率下始终为-90°。因此,对于二阶低通滤波器,截止频率对应于奈奎斯特曲线与负虚轴相交的点。
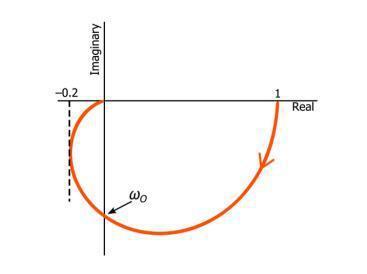
二阶奈奎斯特图中的Q因子
即使是如上所示的基本奈奎斯特图也可以提供关于二阶滤波器Q因子的重要定性信息。如果正在处理无源低通滤波器,那么可以假设低频增益将是统一的。因此,奈奎斯特曲线将以幅度响应1开始,并且由于在非常低的频率下相移基本上为零,因此奈奎斯特迹线源自正实轴上的值1。
当频率增加时,曲线离开实轴后的操作会给我们提供关于幅度响应的信息,而这反过来又会给我们关于Q的信息。首先,如果距离原点的距离增加超过初始值,当输入频率接近截止频率时,滤波器的增益会增加,因此Q必须足够高才能产生一些峰值。
此外,通过比较截止频率下的增益和初始增益,可以形成截止频率区域中幅度响应的一般概念。如果截止频率增益明显高于低频增益,则您知道滤波器具有相对较高的Q值。下图显示了具有相同截止频率但不同Q的RLC滤波器的两条奈奎斯特曲线。橙色曲线表示一个临界阻尼滤波器,即Q=0.5,ωo处的增益为-6 dB。蓝色曲线表示欠阻尼滤波器;其Q系数约为1.7,ωo处的增益为+4.7 dB。
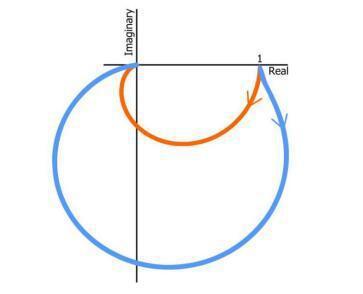
总结
我们已经看到,用于低通滤波器的奈奎斯特图给出了关于传递函数中极点数的清晰、直接的信息,并且我们探讨了奈奎斯特曲线的一般形状与二阶滤波器的Q因子之间的关系。
-
电容器
+关注
关注
64文章
6217浏览量
99534 -
电感器
+关注
关注
20文章
2329浏览量
70507 -
谐振放大器
+关注
关注
1文章
15浏览量
12696 -
二阶滤波器
+关注
关注
0文章
7浏览量
8200 -
RLC电路
+关注
关注
2文章
26浏览量
7162
发布评论请先 登录
相关推荐
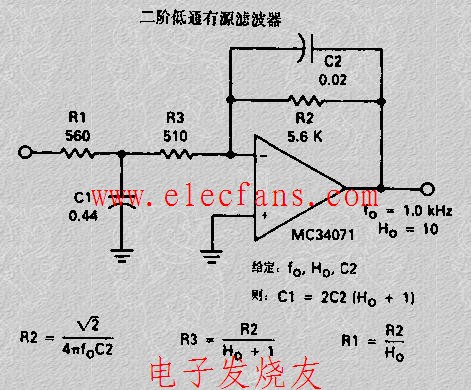
二阶有源滤波器设计





 二阶滤波器的奈奎斯特图简析
二阶滤波器的奈奎斯特图简析











评论