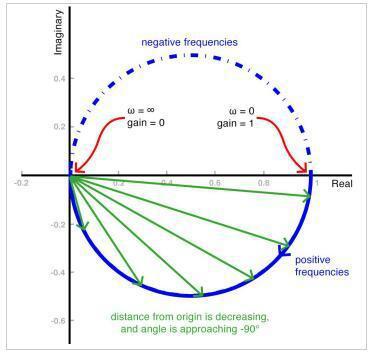
我们看到系统的频率响应可以用极坐标图表示,其曲线表示频率从零到无穷大变化的幅度和相位。我们称之为奈奎斯特图(或奈奎斯特图),它是更常见的波德图的有趣替代品。它提供了我们可以从一阶滤波器的奈奎斯特图中提取的一般信息。
截止频率的重要性
上图不包括一条非常重要的信息,即滤波器的截止频率。一阶低通滤波器的s域传递函数可表示如下:

这个公式告诉我们,一个给定的低通滤波器的唯一的显着特点是和ωo。参数K是滤波器的低频增益。无源元件没有能力放大的信号,所以,如果我们只关心RC一阶低通滤波器,我们可以忽略,因为它永远是1,其余参数ωo是截止频率。因此,我们可以简单地通过指定截止频率来完整地描述RC低通滤波器。
找到截止频率
奈奎斯特曲线肯定没有我们从波德图中很好地了解到的典型的衰减特性,事实上,奈奎斯特图并没有给出关于滤波器电路截止频率的具体信息。然而,检查截止频率和奈奎斯特曲线之间的关系是加强截止频率概念的一种好方法,它也将使我们对奈奎斯特方法在视觉上描绘频率响应的局限性有所了解。首先,我们需要考虑关于幅度响应和相位响应的截止频率实际发生的情况。
通过幅度的截止频率
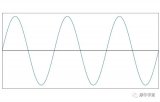
你可能知道截止频率的另一个名称是3db(或-3db)频率,这提醒我们,当输入频率为ωo时,一阶低通滤波器提供3db的衰减(或相当于-3db的增益)。我们在奈奎斯特图中不使用分贝,因此代替为-3db,使用相应的振幅比即1/√2。当我们处理极坐标图时,我们应该始终注意三角形;例如,复数的大小是确定的,就好像它是直角三角形的斜边,直角三角形的两条边是实部和虚部,我们使用三角法来计算复数。既然你在考虑三角形,那么系数1/√2有什么想法吗?

如上图所示,当一个直角三角形有两条等长的边时,就需要用到因子√2。如果我们把边的长度减到0.5,斜边的长度就是√2×0.5,也就是1/√2。

那么,这意味着什么?考虑以下奈奎斯特图:

这是一阶低通滤波器的奈奎斯特图。请注意,没有包括与负频率对应的曲线部分。
如你所见,滤波器在曲线的最低点有1/√2的增益,其中实部分量的绝对值等于虚部分量的绝对值,这是一阶低通滤波器奈奎斯特图中截止频率的位置。同样的关系也适用于一阶高通滤波器,但在这种情况下,截止频率在曲线的最高点:

不同之处在于,随着频率的增加,高通滤波器的相移从+ 90°变化到0°,而低通滤波器的相位在0°到-90°之间变化。因为角度是从正实轴逆时针测量的,所以在实轴上方绘制正相移,在实轴下方绘制负相移。另请注意,两个图的箭头指向相反的方向:在低通图中,箭头指向原点,因为随着频率的增加,增益会减小;在高通图中,它指向远离原点,因为随着频率的增加,增益会增加。
通过相移实现截止频率
如果我们回想起由一阶滤波器产生的90°相移以截止频率为中心,我们也可以在奈奎斯特图中找到截止频率。换句话说,在相移ωo是+ 45°或-45°。在复平面中绘制的矢量在其实部和虚部具有相等的绝对值时将具有+ 45°或-45°的角度,这导致我们从幅度响应的角度考虑截止频率时发现的相同几何关系。


奈奎斯特图中截止频率的总结
你可能已经注意到,这些奈奎斯特图中截止频率的位置是纯几何的。你不能将固定频率值附加到该位置,因为每个一阶低通滤波器或每个一阶高通滤波器的位置都相同。奈奎斯特图显然不是波特图的替代品;然而,它是一种更直接的方式来传达有关系统传递函数的信息,正如我们将在之后的文章中看到的那样,它是稳定性分析中的一个方便工具。
-
低通滤波器
+关注
关注
14文章
474浏览量
47447 -
衰减器
+关注
关注
4文章
640浏览量
34373 -
高通滤波器
+关注
关注
0文章
97浏览量
11057
发布评论请先 登录
相关推荐
奈奎斯特图分析怎么判断稳定性啊?
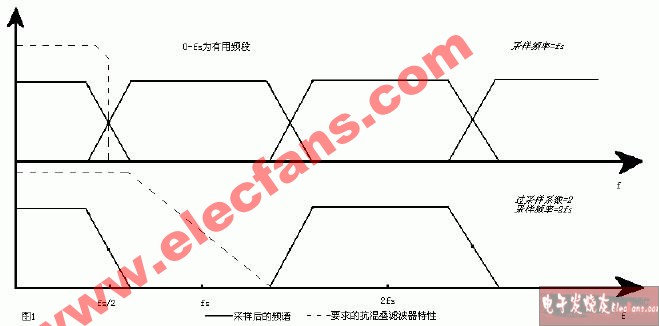
光电编码器在最高转速时,输出频率为20KHZ,用DSP进行转速采集,需要满足“奈奎斯特”采样定理吗?
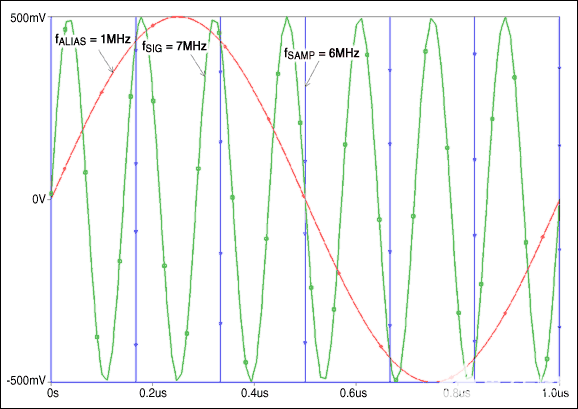
超越第一奈奎斯特区域,将那奎斯特混叠变为优势
奈奎斯特采样定理




 你了解奈奎斯特图中的截止频率吗?
你了解奈奎斯特图中的截止频率吗?
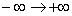











评论