2.1
时域
时域是真实世界,是唯一实际存在的域。
时域就是我们经历的现实世界,高速数字产品运行于其中。当评估数字产品的性能时,通常在时域中进行分析。因为产品的性能最终要在时域中测量。
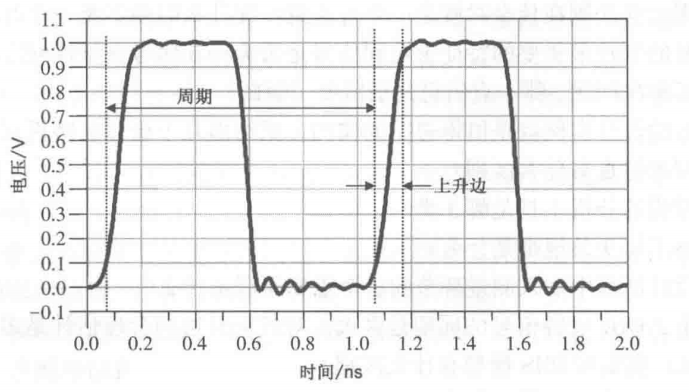
时钟周期就是时钟循环重复一次的时间间隔,通常用ns(纳秒)度量。时钟频率F,即1s内时钟循环的次数,是时钟周期T的倒数,即F=1/T。
上升边与信号从低电平跳变到高电平所经历的时间有关,通常有两种定义。一种是10%-90% 上升边,指信号从终值的10%跳变到90%所经历的时间。第二种定义方式是20% ~ 80%上升边,这是指信号从终值的20%跳变到80%所经历的时间。
2.2
频域
频域不是真实的,而是一个数学构造。时域是唯一客观存在的域,而频域是一个遵循特定规则的数学世界。
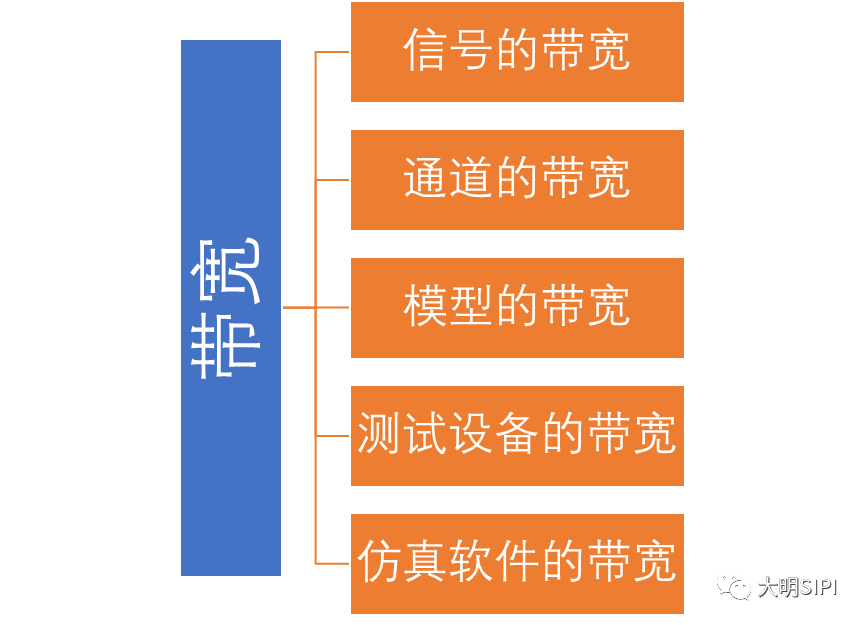
在频域中理解和描述一些问题要比在时域中更容易。例如,带宽就是一个频域的概念,我们用它描述与信号、测量、模型或互连相关的最高有效正弦波频率分量。
运用傅里叶变换能够将波形从时域变换到频域。
2.3
正弦波的特征
正弦波是频域中唯一存在的波形。通常选择在频域中使用正弦波,是因为时域中的任何波形都可用正弦波合成。

用频率、幅度和相位3项可以充分描述正弦波。
频率通常用f来表示,指每秒中包含完整正弦波的周期数。幅度是中间值之上最大的波峰高度值。相位是在时间轴起点的波的起始位置。
在时域中可能要用上千个电压-时间数据点表示波形,在频域中则变换为一个幅度-频率数据点,这样描绘正弦波就简单多了。
2.4
理想方波的频谱
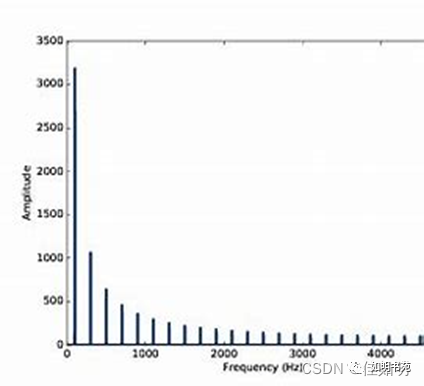
理想方波的上升边为0,占空比是50%,峰值为1V,重复频率为1GHz,其频谱中的正弦波频率就是1GHz的整倍数。采用离散傅里叶变换计算出各个频率分量的幅度。所有偶次谐波的幅度都为零,只有奇次谐波具有非零值。还有一个特殊的频率点:0Hz。
因为正弦波的均值为零,任何正弦波的组合也只能描述时域中均值为零的波形。如果容许一个直流偏移,即波形的均值为非零值,直流分量就在零频率点上。有时也称为0次谐波,其幅度与信号的均值相等。在方波占空比为50%的情况下,0次谐波的幅度为0.5V。
正弦波频率分量及其幅度的集合称为频谱,每一分量称为谐波;任何谐波的幅度都可由2/(nπ)计算得出。

2.5
从频域逆变换到时域
在频域中,频谱表示时域波形包含的所有正弦波频率幅度。如果知道频谱,要想观察它的时域波形,则只需将每个频率分量逆变换成它的时域正弦波,再将其全部叠加即可。这个过程称为傅里叶逆变换。


-
正弦波
+关注
关注
11文章
648浏览量
55577 -
信号完整性
+关注
关注
68文章
1416浏览量
95598 -
傅里叶变换
+关注
关注
6文章
442浏览量
42687
发布评论请先 登录
相关推荐




 信号完整性的时域和频域简析
信号完整性的时域和频域简析
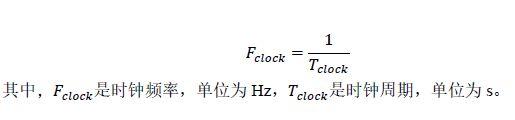















评论