4.1
阻抗的定义
我们把阻抗定义为电压和电流之比,通常用大写字母Z表示。Z = V/I。在信号完整性扮演重要角色的高速数字系统中,信号是指变化的电压或变化的电流。所有信号完整性的问题都是由模拟信号(变化的电压和电流)与互连电气特性之间的相互作用引起的,而影响信号的关键电气特性是互连的阻抗。
阻抗是描述互连的所有重要电气特性的关键术语,知道了互连的阻抗和传播时延,也就知道了它的几乎所有电气特性。阻抗是一个通用术语,适用于时域和频域中的所有电路元件。
阻抗有两个极端的情况。一种是开路元件,没有电流流过。如果在元件两端加任意电压, 而流过的电流是零,这个元件的阻抗就是Z = 1 V/0 A = ∞ Ω,即开路元件的阻抗非常大;另一种是短路元件,无论流过它的电流有多大,其两端的电压都是零,所以短路元件的阻抗为Z = 0 V/1 A = 0 Ω。
4.2
阻抗的作用
阻抗是解决信号完整性问题方法学的核心。为了把物理系统设计成我们希望的最佳性能,就需要把所设计的物理结构转化为与之等效的电路模型。这个过程称为建模。
所建电路模型的阻抗决定了互连怎样影响电压和电流信号。只要建立了电路模型,就能使用电路仿真器(如 SPICE)预估电压源受到互连阻抗影响后的新波形。或者,使用驱动器及互连行为模型预估信号与阻抗相互作用行为的性能。这个过程称为仿真。
最后,分析预估的波形以确定它们是否满足时序、失真或噪声指标,它们是否合格,或者物理设计是否需要修改。建模和仿真这两个关键步骤的基础是:把物理特性转换成阻抗描述,分析阻抗对信号的影响。
如果知道电路图中每个电路元件的阻抗,并且知道如何计算组合电路元件的阻抗,任何模型和任何互连的电气特性就都能加以估算。所以,阻抗在信号完整性分析的各个方面都非常重要。
4.3
实际电路元件与理想电路元件
实际元件是可测的,是实际存在的事物,它们是构成现实硬件系统的互连或元件。实际元件包括板上的线条、封装中的引线,或装在板上的去耦电容器等。
理想元件是对具有特定精确定义的专用电路元件的数学描述。每个理想电路元件都具有非常特定的模型,或者说对相关行为的定义。模型是仿真器所能理解的语言。只要将理想电路元件加以组合,就可以构建出电路。
通常,仿真器只能仿真由理想电路元件描述的电路。理想元件的组合构成了模型。电路理论的形式和功能只适用于理想元件。
为了描述任何实际的互连,在建模时要用到如下4种理想的两端电路元件:
前三种可归为一类,因为它们的特性可以集中到一个点上,所以把它们称为集总电路元件。它们与理想传输线的特性不同,后者的特性沿着传输线是“分布式的”。
这些理想的电路元件都有准确的定义,其定义描述了它们如何与电流、电压相互作用。
4.4
时域中的阻抗
理想电阻器的阻抗即电阻器的阻值。这就是说,理想电阻器的阻抗是恒定的,并且与电压和电流无关。其阻抗为:
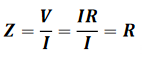
如果电容器两端的电压变化很快,流过的电流就会很大。如果电压几乎不变,流过的电流也就接近于零。利用这个关系,可以在时域中计算出理想电容器的阻抗:
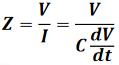
它表明电容器的阻抗与它两端电压波形的确切形状有关。如果电压波形的斜率很大(即电压变化很快),则流过的电流就很大,而且电容器的阻抗会很小。同样也表明,在电压信号的变化率相同时,电容器的电容值越大,它的阻抗就越小。
理想电感器的阻抗:
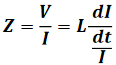
如果流过电感器的电流迅速地增加,阻抗就很大,如果流过的电流只有很微弱的变化,电感器的阻抗就非常小。对于直流电流来说,电感器的阻抗近似为零。
4.5
频域中的阻抗
频域的重要特征就是正弦波是其中唯一存在的波形。在频域中,只能通过研究理想电路元件怎样与正弦波(即包括正弦电压和正弦电流)相互作用,进而描述这些理想电路元件的行为。
可以在电路元件两端加上正弦电压,然后观察流经这个电路元件的电流。这时仍采用阻抗的基本定义(即电压和电流之比),所不同的是采用了两个正弦波之比,即电压正弦波和电流正弦波之比。
任何电路元件的阻抗由两个数组成:在每个频率点上的幅值和相位。阻抗的幅值和相位都与频率有关,它们都可能随频率的变化而变化。所以,在描述阻抗时,需要指出它是在哪个频率下的阻抗。
如果施加正弦电流使之流过电阻器,在电阻器两端就会得到一个正弦电压,它是R和正弦电流的乘积:
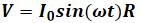
这个阻抗与频率无关,且相移为零。在任何频率上,理想电阻器的阻抗都是相等的。这和在时域中看到的结果完全一致。
理想电容器阻抗:
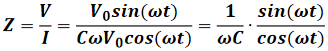
其幅值就是1/ωC,当角频率增加时,电容器的阻抗就会减小。这就是说,虽然电容器的电容是个不随频率变化的常数,但阻抗随着频率的升高会减小,因为随着频率的升高,流经电容器的电流会增大,从而阻抗就减小了。
理想电感器的阻抗在频域中的表达式为:
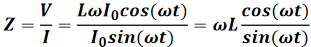
尽管电感值是个不随频率变化的常数,阻抗的幅值ωL却随着频率的升高而增大。所以频率越高,交流电流要流经电感器就越困难,这是电感器特性所产生的结果。
理想电阻器的电阻、理想电容器的电容和理想电感器的电感,都是不随频率变化的常数。对于理想电阻器,阻抗也是不随频率变化的常数。然而,对于电容器而言,阻抗随着频率的升高而减小,而电感器的阻抗随着频率的升高而增大。
4.6
等效电路模型
实际互连的阻抗行为可以通过对理想元件的组合得到非常好的近似。理想电路元件的组合称为等效电气电路模型,或简称为模型,电路模型图通常称为原理图。
等效的电路模型有两个特征:一是给出电路元件怎样连接在一起(称为拓扑结构);二是确定每个电路元件的值(称为参数值或寄生值)。对于每个模型,经常会提出两个重要的问题:它的优质度和带宽是多少?
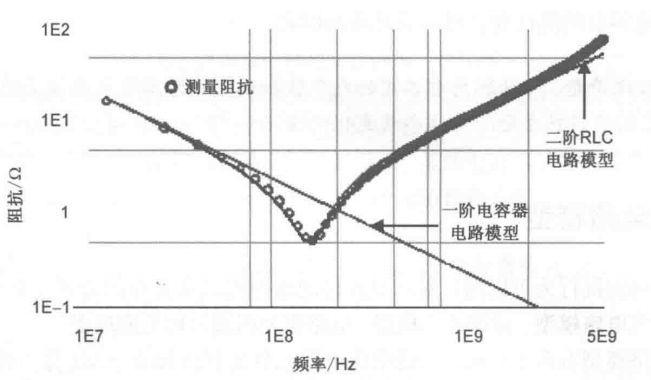
对于实际电容器而言, 更准确的模型就是理想电容器、电感器和电阻器的串联。
通常把建立的最简单模型称为一阶模型,它作为起始的第一步。复杂度增加的模型与实际元件更加吻合,我们把以后相继建立的模型称为二阶模型、三阶模型等。
-
电容器
+关注
关注
64文章
6202浏览量
99310 -
驱动器
+关注
关注
52文章
8156浏览量
146006 -
电阻器
+关注
关注
21文章
3759浏览量
62039 -
信号完整性
+关注
关注
68文章
1397浏览量
95383 -
等效电路
+关注
关注
6文章
292浏览量
32730
发布评论请先 登录
相关推荐
DAC信号完整性浅析 DAC信号完整性解决方案
【下载】《信号完整性与电源完整性分析》——高速PCB人员的必备书籍,EMI经典之作
TDR阻抗测量-信号完整性的基础

信号完整性计算和器件的特性阻抗研究
信号完整性简介及protel信号完整性设计指南

基于IBIS模型的信号完整性分析





 信号完整性-阻抗与模型浅析
信号完整性-阻抗与模型浅析













评论