13.1 传输线的一阶模型
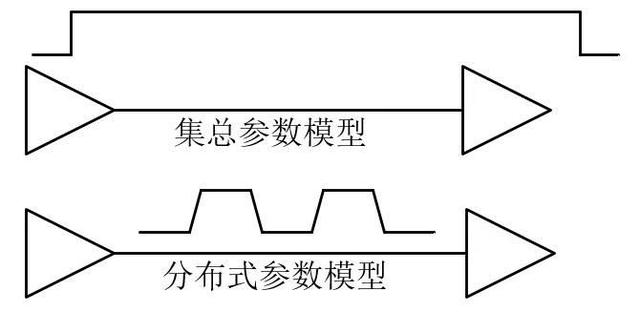
理想传输线是一种新的理想电路元件,它有两个重要的特征:恒定的瞬时阻抗和相应的时延。这个理想模型是连续分布式模型,因为理想传输线的各个特性分布在整条传输线上,而不是集中在一个集总点上。
从物理上讲,可控阻抗传输线是由两条一定长度且横截面均匀的导线组成的。前面介绍了零阶模型,它把传输线描述成一系列相互有一定间距的电容器的集合。然而这仅是物理模型,并不是等效电气模型。
把信号路径和返回路径导线的每一小节描述成回路电感,就能进一步近似物理传输线。如下图所示,这个最简单的传输线等效电路模型中,每两个小电容器就被一个小回路电感器隔开。图中C表示两条导线之间的电容,L表示两小节之间的回路电感。
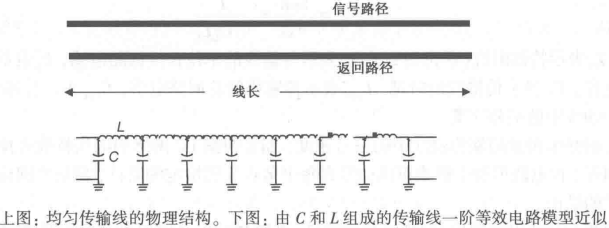
每一节信号路径或返回路径都有各自的局部自感。在两个分立电容器之间的两节信号路径-返回路径之间又存在局部互感。对于非平衡传输线,如微带线,每一节中信号路径的局部自感与返回路径的局部自感是不同的,其中信号路径的局部自感要比返回路径的局部自感大10倍以上。
但是对信号而言,当它在传输线上传播时,实际传播的是从信号路径到返回路径的电流回路。从这种意义上讲,所有信号电流流经的一个回路电感,由信号路径节和返回路径节构成。对于传输线上的信号传播和大多数串扰而言,信号路径和返回路径的局部电感并不怎么重要,只有回路电感才是重要的。当把理想的分布传输线近似为一系列的LC电路时,模型中表示的电感实际上就是回路电感。
由C和L组成的传输线一阶等效电路模型是理想传输线的近似。在极端的情况下,若电容器和电感器的尺寸逐渐减小而节数逐渐增多,近似程度就会更好。
在极端情况下,当电容器和电感器无穷小,而LC电路的节数趋于无穷时,单位长度电容C_L和单位长度电感L_L都为常数。这两个参数通常称为传输线的线参数。
信号沿网络传输时,在每节点上都受到恒定的瞬时阻抗。这个瞬时阻抗与理想分布传输线元件的瞬时阻抗是一样的,它在数值上与导线的特性阻抗相等。同理,从信号进入LC网络到信号输出会有一个有限的时延。
根据传输线的线参数和总长度,可以计算出传输线的特性阻抗和时延,即:
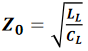
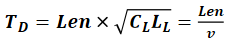
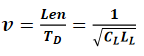
因为信号的速度取决于材料的介电常数、单位长度电容和单位长度电感,所以可将单位长度电容与单位长度电感关联如下:
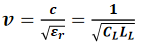
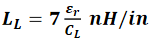
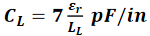
从特性阻抗和速度的关系,可以得出下列关系式:
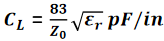
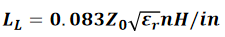
从传输线的时延和特性阻抗,可以得出下列关系式:
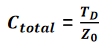
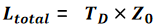
其中,Z_0表示特性阻抗(单位为Ω),L_L表示传输线的单位长度回路电感(单位为nH/in),C_L表示传输线的单位长度电容(单位为pF/in),T_D表示传输线的时延(单位为ns),L_total表示传输线的总回路电感(单位为nH),C_total表示传输线的总电容(单位为pF),v表示传输线中的信号速度(单位为in/ns)。
所有介电常数为4的50Ω传输线,其单位长度电容都相同,约为3.3 pF/in。单位长度回路电感也都相同,约为8.3nH/in。
当信号边沿快速传播时,它既没看到电容C和实现充电所需的时间常数RC,也没看到电感L和导致上升边变慢的时间常数L/R。相反,它看到了一种崭新的优异特质,即可以支持传输任何上升边信号的瞬时阻抗。对边沿信号而言,传输线看上去既不像电感,也不像电容,它像一个电阻性元件。
13.2 特性阻抗的近似计算
设计一个指定的特性阻抗,实际上就是不断调整线宽、介质厚度和介电常数的过程。如果知道传输线的长度和导线周围材料的介电常数,计算出特性阻抗并运用上面的关系式,就可以计算出其他所有参数。
经验法则 :FR4板上50Ω微带线的线宽等于介质厚度的2倍。而50Ω带状线的两平面之间的总介质厚度等于线宽的2倍。
对于微带线,推荐的通用近似式为:
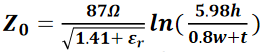
对于带状线,推荐的通用近似式为:
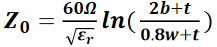
其中,Z_0表示特性阻抗(单位为Ω),h表示信号线与平面之间的介质厚度(单位为mil),w表示线宽(单位为mil),b表示平面之间的距离(单位为mil),t表示金属厚度(单位为mil),ε_r表示介电常数。
在一阶模型中,微带线和带状线的特性阻抗与介质厚度和线宽的比值成比例变化。只要这个比值保持不变,特性阻抗就恒定不变。
13.3 n节集总电路模型
根据理想传输线的时延,可以估算出n节集总电路模型的带宽。LC模型的节数越多,带宽就越高。一节模型的带宽只有第一个谐振频率的1/4,两节模型的带宽为第一个谐振频率的1/2,16节模型的带宽为第4个谐振频率。我们可以归纳出吻合的最高频率,即模型的带宽为:
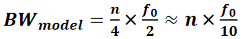
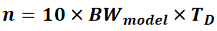
其中,BW_model表示n节集总电路模型的带宽,n表示模型中LC的节数,T_D表示传输线的时延,f_0表示全波的谐振频率, f_0=1/T_D 。
要使模型的带宽达到1/T_D,需要10节LC电路。也就是说,因为这个频率相当于传输线上仅有一个全波,为了更好地近似,每1/10个信号波长就必须对应1节LC电路。
例如,如果互连的时延T_D=1ns,要求n节LC近似模型的带宽为5GHz,则至少需要**n=10×5GHz×1ns=50**节。在最高频率时,传输线上有**5GHz×1ns=5**个波长。每个波长需要10节,因此要获得较好的近似效果,需要**5×10=50**节LC电路。
我们也可以估算出用单个LC电路近似传输线时的带宽有多高。或者说,在多高的频率范围内,传输线可以近似成单个LC电路。单个LC电路的带宽为:
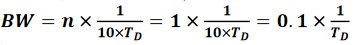
传输线的时延越长,可以用单个LC模型近似的频率就越低。
如果信号的上升边为RT,则信号的带宽(最高有效正弦波频率成分)为:
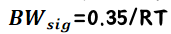
如果传输线的时延为T_D,并用n节集总电路模型来近似,那么必须确保模型的带宽BW_model应至少大于信号带宽BW_sig,即:
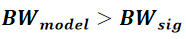
即:
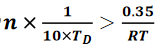
即:
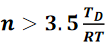
其中,BW_sig表示信号的带宽,BW_model表示模型的带宽,RT表示信号的上升边,T_D表示传输线的时延,n表示准确模型所需LC电路的最少节数。
如果上升边等于传输线的时延,则此传输线的准确模型至少需要3.5节LC电路。在这种情况下,上升边的空间延伸就等于传输线的长度。
经验法则 :当给定上升边RT(单位为ns)值时,n节LC集总电路模型为了达到足够高的带宽,每节LC电路对应的线长(单位为in)值必须小于1.7×RT。
当然,无论是在低频还是在高频,理想分布传输线模型总是均匀互连的更好模型。
本节评估了依据信号带宽及其精确度,在对实际传输线建模时所需LC电路的最少节数。但这仍是带宽受限下的一种近似做法。在为实际传输线选配模型时,可以根据对特性阻抗和时延的要求,先定义一个理想传输线作为首选。在非常罕见的情况下,当问题也是用L或C值表征的时候,就可以采用上述的n节集总参数模型来模拟真实的传输线。但是,还是从一个理想传输线模型先建模。
13.4 特性阻抗随频率的变化
到目前为止都假设传输线的特性阻抗与频率无关。但是,我们已经知道,从传输线前端看进去的输入阻抗与频率有密切的关系。毕竟,在低频情况下,远端开路传输线的输入阻抗看上去像一个电容器,起初阻抗较高,再下降到很低。
假设随着频率的变化,互连的介电常数是个常数,那么单位长度电容也恒定不变。虽然在某些情况下,介电常数会有微小的变化,但对大多数材料而言这个假设是合理的。
由于趋肤效应的影响,单位长度电感会随频率而变化。实际上,在低频时回路电感比较高,但是随着越来越多的电流分布在外表面,回路电感将下降。这说明,在低频时特性阻抗比较高,随着频率的升高,特性阻抗将下降到某一恒定值。
使用二维场求解器,可以计算出1盎司铜制成的50Ω微带线的特性阻抗与频率的关系,在低频时特性阻抗比较高,约在1MHz开始下降,且直到50MHz以前都一直在下降。从直流到高频,特性阻抗的总下降量约为7Ω,即变化小于15%。
约50 MHz以上时,传输线的特性阻抗是个常数,不再随频率变化。这个值就是通常用于估计各种高速信号性能的“高频”特性阻抗。
-
电容器
+关注
关注
64文章
6376浏览量
100886 -
电感器
+关注
关注
20文章
2348浏览量
71181 -
信号完整性
+关注
关注
68文章
1420浏览量
95973 -
传输线
+关注
关注
0文章
377浏览量
24283 -
微带线
+关注
关注
2文章
82浏览量
16516
发布评论请先 登录
相关推荐
【连载笔记】信号完整性-传输线物理基础及其分类
基于IBIS模型的信号完整性分析

信号完整性基础--传输线(一)




 信号完整性-传输线的模型简析
信号完整性-传输线的模型简析
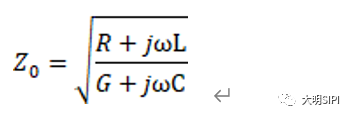












评论