T-Coil的原理和应用

曾经T-Coil被用于商业机密隐藏了数十年，后来技术被公开，可以看到这个技术的确是一个非常令人震惊的技术，本篇文章分析了T-Coil的原理和应用，并且将功能全部集成在小程序中。

T-Coil设计

背景

T-Coil技术首先由Ginzton于1948年首次提出，目的是改善分布式放大器的匹配，比较有趣的是这篇文章的署名有HP的创始人之一Hewlett，但是这项技术被Tek的工程师所发掘，并且用在了示波器的前端，作为HP的商业竞争对手保守技术秘密数十年，直到1960年代才由Tek工程师公开。

如下是摘自上面的一段话：

Tek felt, rightly, that having the T-coil equations for the lossy, asymmetrical case was equivalent to having nukes when everyone else only had rocks and pointy sticks, so they kept this knowledge as a trade secret. The T-coil was one important bit of magic that allowed Tektronix to maintain such a lead on everybody else, because they could get double or triple the gain-bandwidth product out of an amplifier just by adding a capacitor and a pair of coupled inductors in the right place.

Tek公司感到，拥有掌握了带损耗、非对称情况的T-线圈方程等同于在其他人在刀耕火种时拥有了核武器，因此他们将这一技术保守为商业机密。T-线圈是使Tek公司保持领先地位的重要法宝之一，因为他们只需在正确的位置添加一个电容和一对耦合电感，就可以将放大器的增益-带宽积提高一倍或三倍。

这里有一个很有意思的发展史，T-Coil技术由Tek工程师John Addis和BOB ROSS发展，并且借助我国的最早在国际刊物上发表数学论文的学者王季同(K. T. Wang, 1875-1948, 其儿女个个都是著名大家)的王氏代数(Wang Algebra)解决了T-Coil公式的推导。

T-Coil

T-Coil实际上是一个特殊的桥T网络，网络拓扑如下：拓扑的变形动画，由桥T-->H桥-->格型网络；

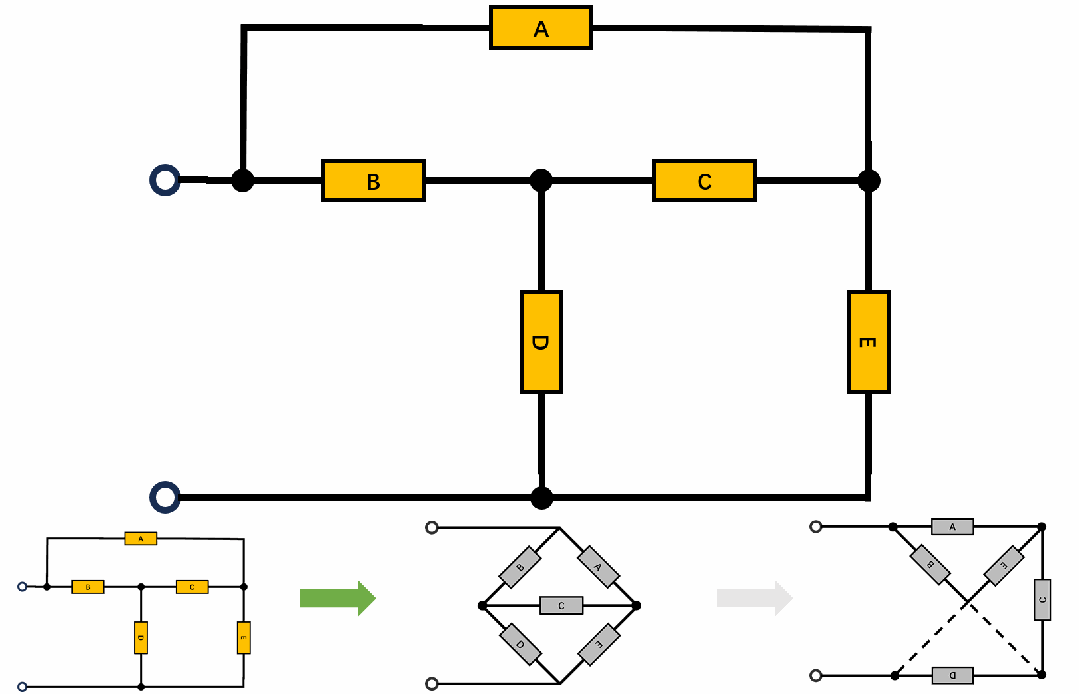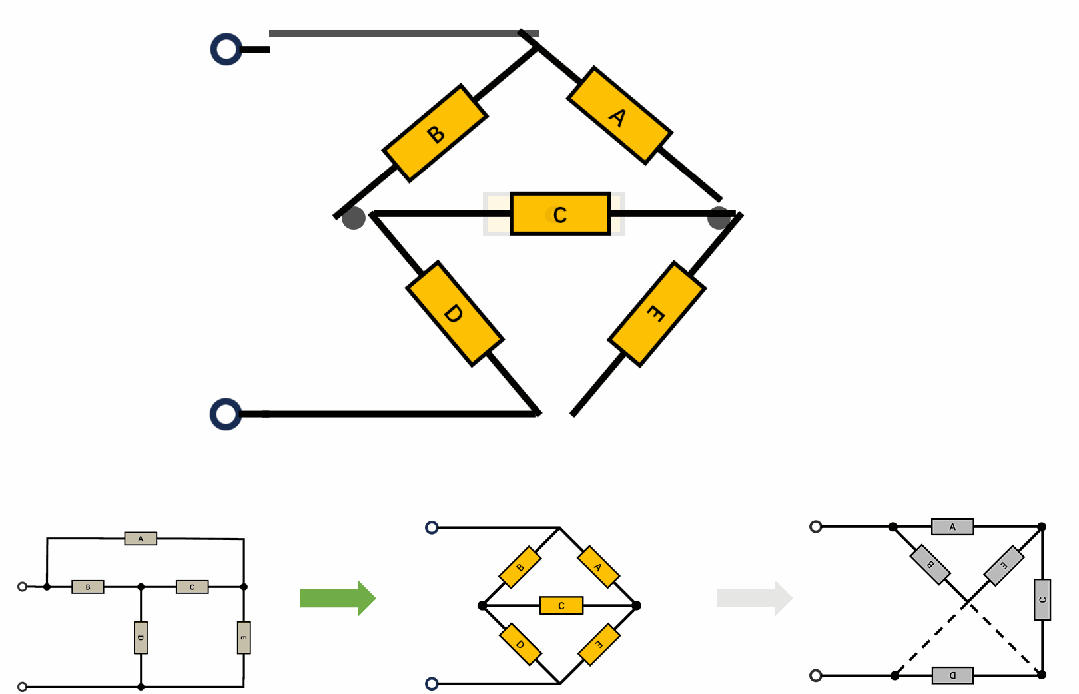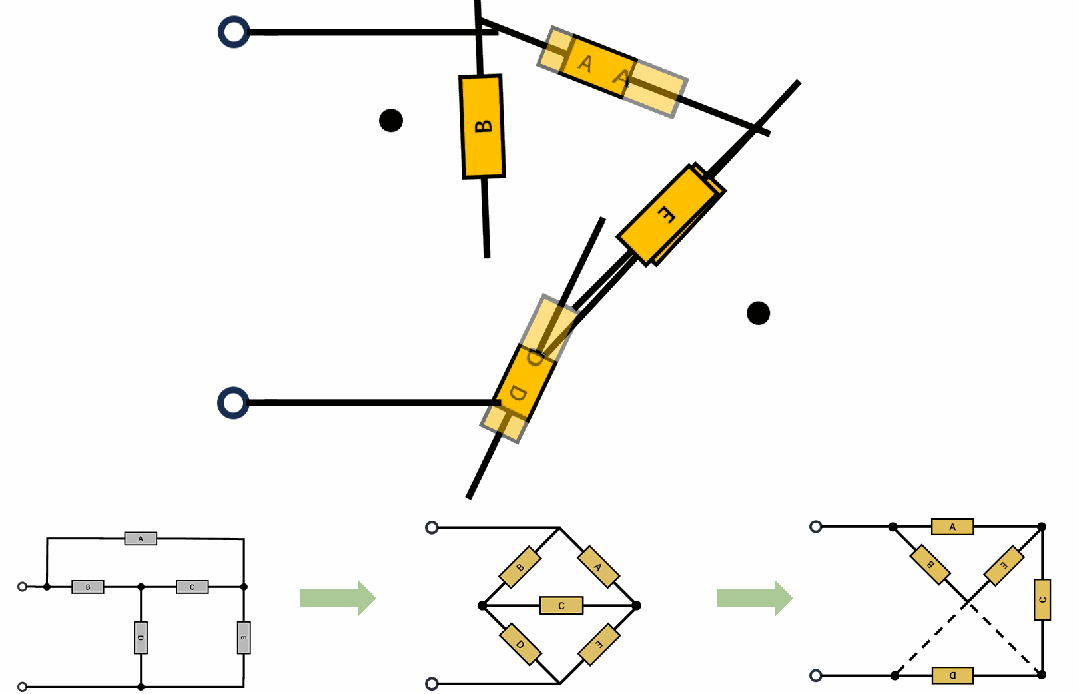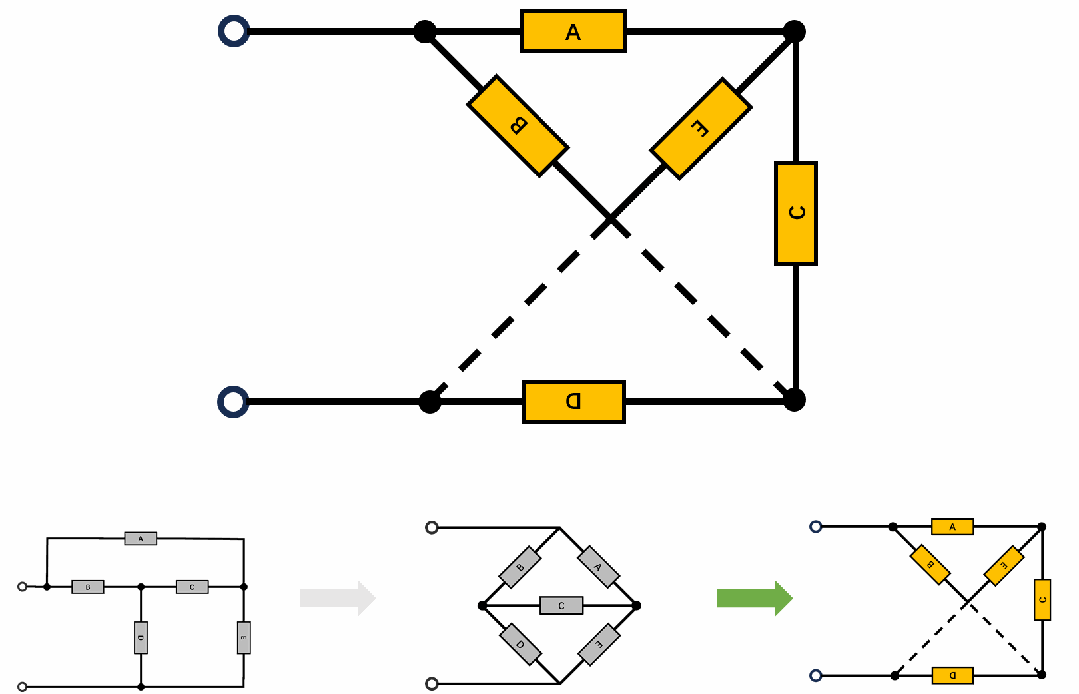
说到这里就不得不提一嘴Zobel网络，Zobel网络是一种均衡器，其特点是输入阻抗是恒定的，T-Coil的设计精髓也在这里，就是其输入阻抗在全频段为恒阻。所以只需要解这个网络，这里有两种计算策略： 1，计算输入阻抗为恒定值

2，计算D支路器件的输出电压，假设D支路负载阻抗为

在T-Coil设计中，上述传输函数是个4阶系统，可以通过零极点抵消的方式，将变为一个2阶系统。而T-Coil就是这拓扑为如下器件的电路结构:

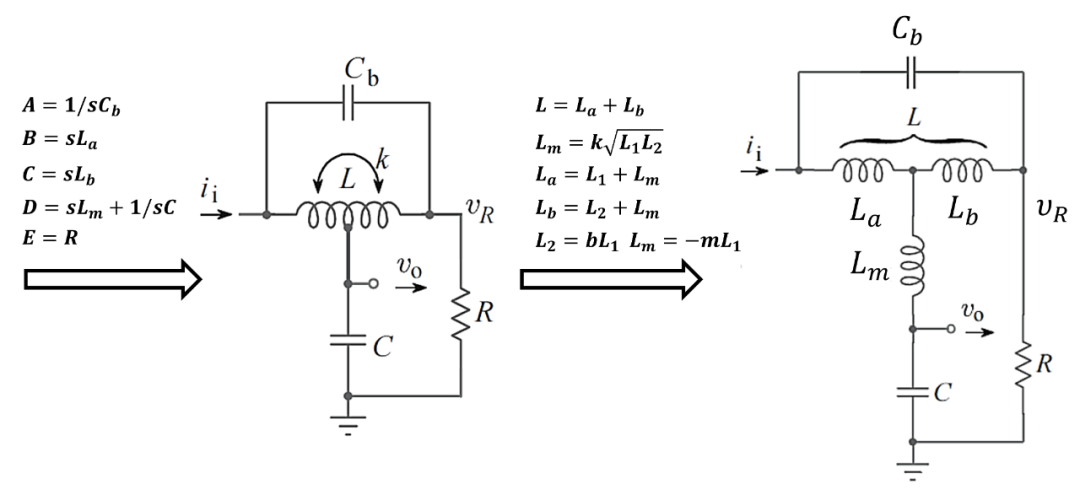
对称(Symmetric)T-Coil

当上图的时就是对称T-Coil，按1计算得到：

公式中有有两个未知数和，所以，有一个自由度设计参数。这里有3种不同的设计约束：

1.从电容上输出，即，优化目标是低通带宽最大

2.从电阻上输出，即，优化目标是全通(恒阻)

3.优化输入匹配，使得输入端口阻抗恒定

从输出，可以得到一个低通特性：

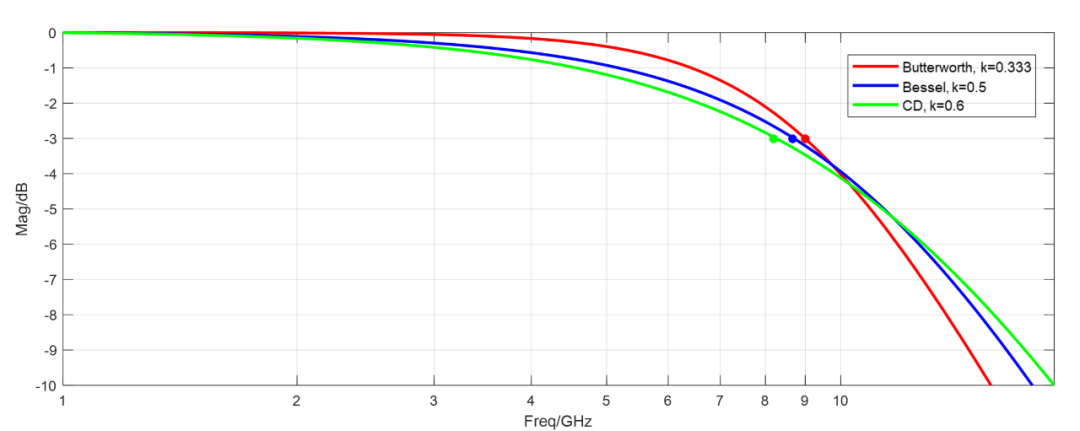
这是一个2个极点的低通滤波器，既然是滤波器，那么我们就可以依据来构造出不同滤波器类型：

当时，是Butterworth低通滤波器(同时T-Coil有最大带宽，带宽是纯RC网络的2.828倍);

当时，是Bessel低通滤波器;

当时，是无过冲的低通滤波器(对应二阶系统临界阻尼);

以下是这几种滤波器的绘图：

对于从输出，这时传递函数为一个全通滤波器(All-pass Filter)：

这意味着从输入端看过去，是看不到电容的，即电容被T线圈中和了，这是由于电容所带来的两个极点刚好在平面的对称位置上由T线圈引入了两个零点，这样零点矢量幅度和极点矢量幅度相等。

注意，T-Coil的带宽扩展能力(BWER, Bandwidth enhancement ratio)注意其前提条件，是电流输入系统中才有2.828倍的带宽提升，但是当在50欧姆匹配的系统中，带宽只有1.414倍提升。

非对称(Asymmetric)T-Coil

非对称T-Coil，即，情况就会变得复杂起来，还是按照上面的思路，一个是从输出，带宽最大，代表是，理论推导证明带宽可以无穷大！另外是输入全频带恒定阻抗匹配，代表是BOB ROSS的恒阻设计。

仅最大化带宽

文献中提到并没有封闭表达式，只能通过数值计算才能进行设计。通过一些处理，实际上是存在封闭表达式的，在这里，不能让输入阻抗恒定来设计了(这意味着非对称T-Coil从输出不是全通)，只能让传输函数的两个零点和两个极点抵消来计算，这样最终传输函数是个二阶的，即最终传输函数为：

上式是是阻尼系数，其实和极点位置密切相关，不同的对应不同的滤波器类型，比如就对应巴特沃斯滤波器类型，就对应贝塞尔滤波器类型，就对应无过冲的临界阻尼状态，令：

整理如下，以下是得到公式：

以下是其他参数：

这种非对称T-Coil有什么优点呢？其优点就是带宽拓展功能变得更加强大，理论上带宽可以拓展到无穷(印度老哥发现的)，实际上从上面的公式也可以看出，当越接近于，那么带宽越大，上式可以验证当时，即时，，和对称T-Coil推导一致。下图是T-Coil带宽扩展(BWER)能力随b的变化情况，当减小，带宽拓展能力迅速上升。

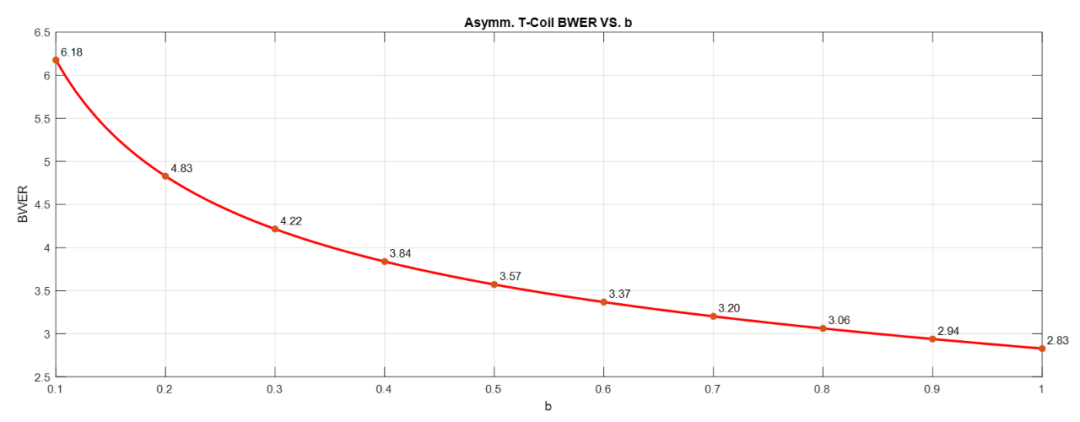
上述公式需要用户预先给定的参数有，当时对应对称T-Coil，当时为非对称T-Coil。

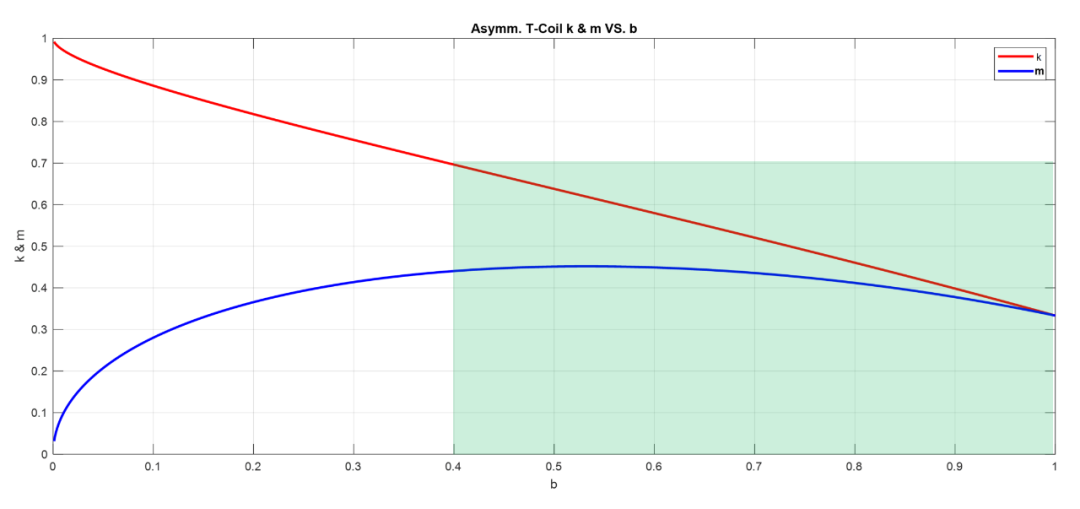
恒阻+2极点设计

BOB ROSS所设计的非对称T-Coil主要考虑实际电路寄生，然后从全通角度出发来优化参数，优点是电路驻波性能优越，带宽也得到提升，考虑到T线圈到负载电容之间有寄生电阻，其中一个分析如下：

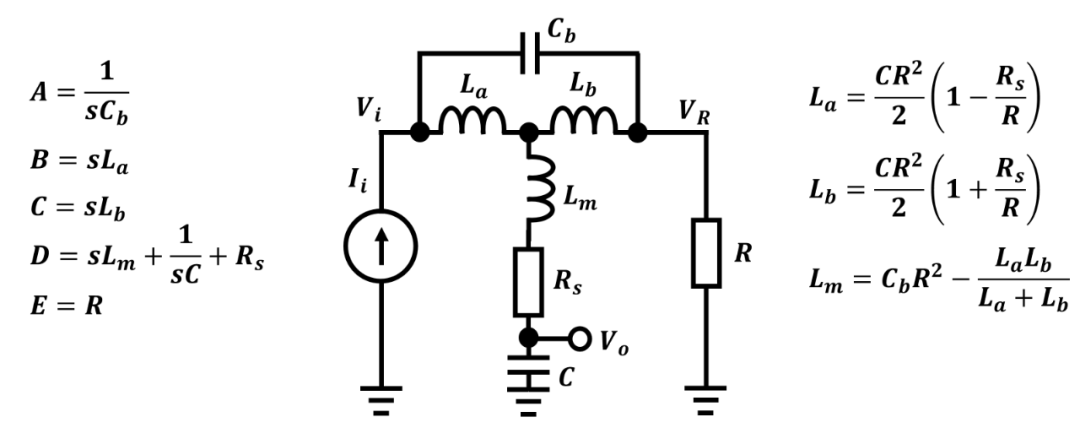
先通过恒定电阻设计，由Matlab符号计算：

%--------------------------------------------------------------------------
% Edited by bbl
% Date: 2023-09-09(yyyy-mm-dd)
% ross constant-resistance T-Coil
% 1, for constant resistance
%--------------------------------------------------------------------------
syms C_b L_a L_b L_m C R s w_n eta b R_s
A  = 1/(s*C_b);
B  = s*L_a;
CC = s*L_b;
D  = s*L_m+R_s+1/(s*C);
E  = R;
Z = A*B*(CC+D+E)+A*CC*(D-E)-E^2*(A+B+CC);
FF0 = collect(Z,'s');
[nn, dd] = numden(FF0);
FF1 = collect(nn,s);
coef = coeffs(FF1, s);
y = solve(coef(1)==0, coef(2)==0, coef(3)==0, L_b, L_m, L_a);
kk = 1;
L_a = simplify(y.L_a(kk))%L_a =(C*R*(R - R_s))/2
L_b = simplify(y.L_b(kk))%L_b =(C*R*(R + R_s))/2
L_m = simplify(y.L_m(kk))%L_m =C_b*R^2 - (C*R^2)/4 + (C*R_s^2)/4=C_b*R^2-L_a*L_b/(L_a+L_b)

运行得到：

再由恒阻约束解输出函数为2阶系统：

%--------------------------------------------------------------------------
% Edited by bbl
% Date: 2023-09-09(yyyy-mm-dd)
% ross constant-resistance T-Coil
% 1, for constant resistance
% 2, for zeros cancellation
%--------------------------------------------------------------------------
syms C_b L_a L_b L_m C R s w_n zeta b R_s
A   = 1/(s*C_b);
B   = s*L_a;
CC  = s*L_b;
D   = s*L_m+R_s+1/(s*C);
E   = R;
Z_D = 1/(s*C);
F = Z_D*(CC*A+E*A+E*B+E*CC)/(CC*A+CC*B+D*A+D*B+D*CC+E*A+E*B+E*CC);
FF0 = collect(F,'s');
[nn, dd] = numden(FF0);
FF = dd*w_n^2*R - nn*(s^2+2*zeta*w_n*s+w_n^2);
FF1 = collect(FF,s);
coef = coeffs(FF1, s);
Nf1 = collect(factor(coef(1)));
Nf2 = collect(factor(coef(2)));
Nf3 = collect(factor(coef(3)));
Nf4 = collect(factor(coef(4)));
NCR1 = L_a - (C*R*(R - R_s))/2;
NCR2 = L_b - (C*R*(R + R_s))/2;
NCR3 = L_m - C_b*R^2 + L_a*L_b/(L_a+L_b);
y = solve(Nf1(end)==0,Nf2(end)==0, Nf3(end)==0,Nf4(end)==0,NCR1==0,NCR2==0,NCR3==0, L_a, L_b, L_m, C_b, w_n);
kk = 1;
L_a  = simplify(y.L_a(kk))% L_a = (C*R*(R - R_s))/2
L_b  = simplify(y.L_b(kk))% L_b = (C*R*(R + R_s))/2
L_m  = simplify(y.L_m(kk))% L_m = (C*(R + R_s)*(R + R_s - 4*R*zeta^2 + 4*R_s*zeta^2))/(16*zeta^2)
w_n  = simplify(y.w_n(kk))% w_n = (4*zeta)/(C*(R + R_s))
C_b  = simplify(y.C_b(kk))% C_b = (C*(R + R_s)^2)/(16*R^2*zeta^2)

运行得到：

这组公式和BOB ROSS计算的一致，当时，其公式和对称T-Coil一致.其中的表示当时的带宽，如果，那么需要使用如下公式计算带宽:

T.T.True专利

在1960年T.T.True提出了另外一种非对称T-Coil电路结构，如下：

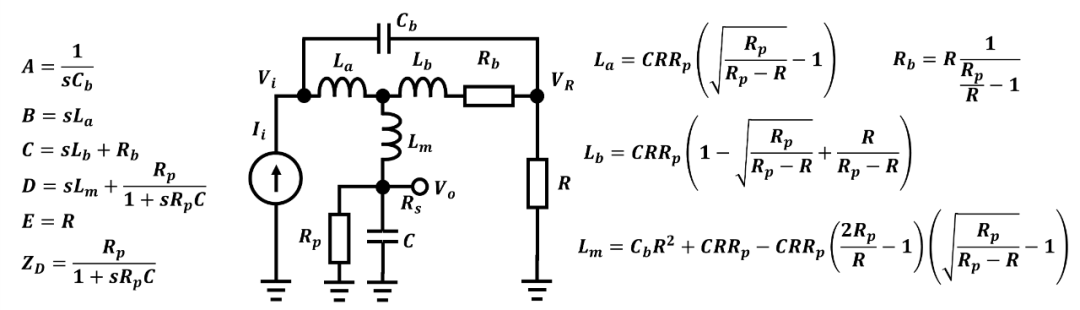
按上述方法计算得到：

T-Coil统一公式

当然上述讨论的T-Coil和实际应用比较还隔着一些寄生参数。另外T-Coil本身还具有寄生电阻，负载也有寄生电阻，所以综合下来就涌现出来非常多的T-Coil的变种，BOB ROSS在最新论文中总结了所有类型的T-Coil，并且发表了预印本(本公众号已经将本文翻译为中文《王氏代数：从理论到实践》)：

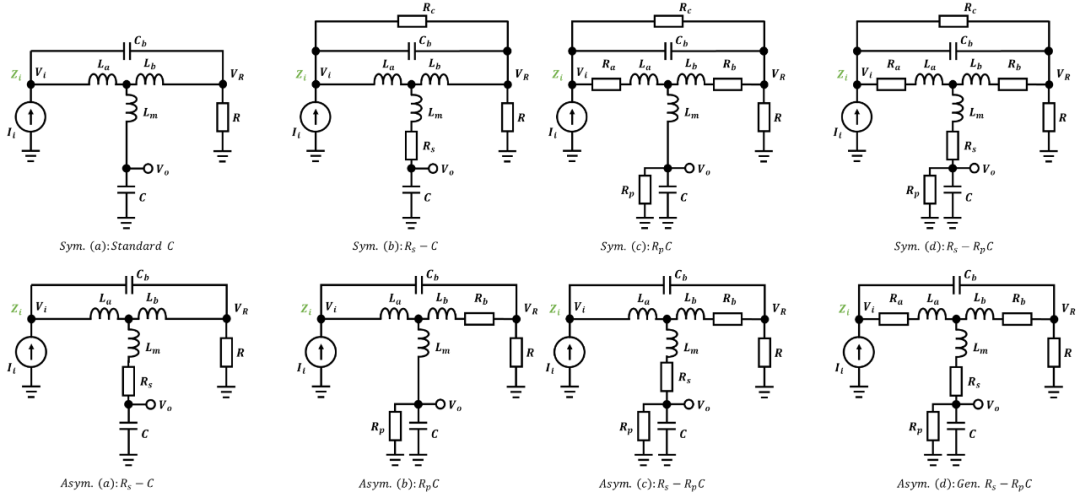
总共有八种不同的情况，小程序中集成了这8种电路结构，可以直接输入参数进行计算。

这里给出通用对称和非对称的matlab计算结果(若对Matlab符号计算感兴趣的同学可以下载，源码提供了直接符号计算T线圈的公式推导过程)：

对称T-Coil

对于:

对于:

非对称T-Coil

对于:

对于，同之前BOB ROSS推导的公式。

上式中的表示从输出的电压增益。

Tips

对于T-Coil的应用应该注意其应用场景，比如在50欧姆系统中，并且从输出，那么带宽展宽就没有2.828了，实际上只有1.414！这是由于在50欧姆系统中，负载和源阻抗并联后就只有原来的一半的电阻了，所以RC带宽也就升高了为原来的2倍。所以T-Coil带宽扩展效应在电流源输入的场景下会更有优势。

当然在50欧姆系统中，从输出就另当别论了，这时系统是全通的，所以从这点上来说T-Coil可以用来屏蔽线路上的电容，这是非常有吸引力的一个特性。

T-Coil的恒阻特性非常有用，尤其在对VSWR有较高要求的地方都可以考虑使用T-Coil.

T-Coil应用

T-Coil的主要应用有：

行波放大器或宽带放大器

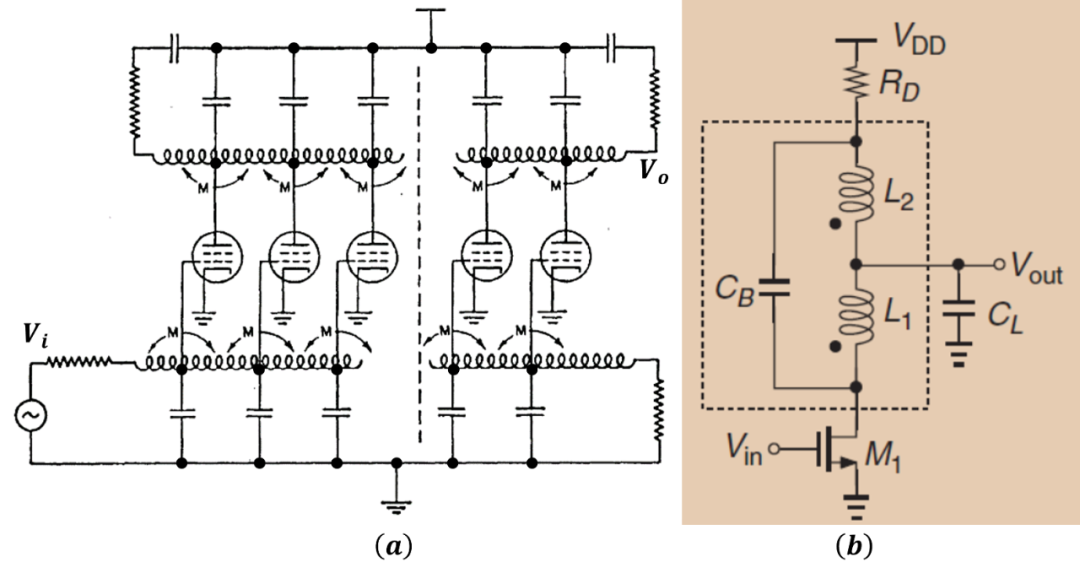
高速IO的ESD设计

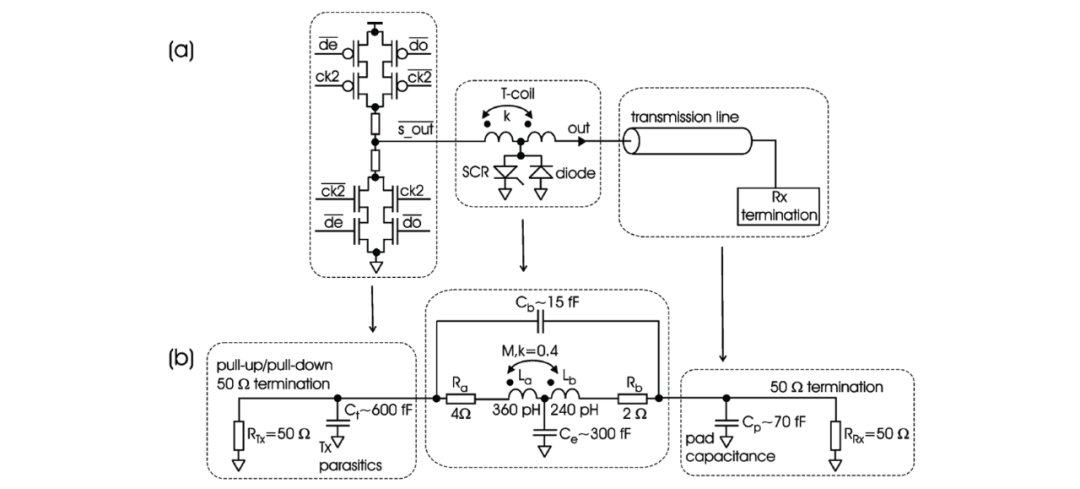
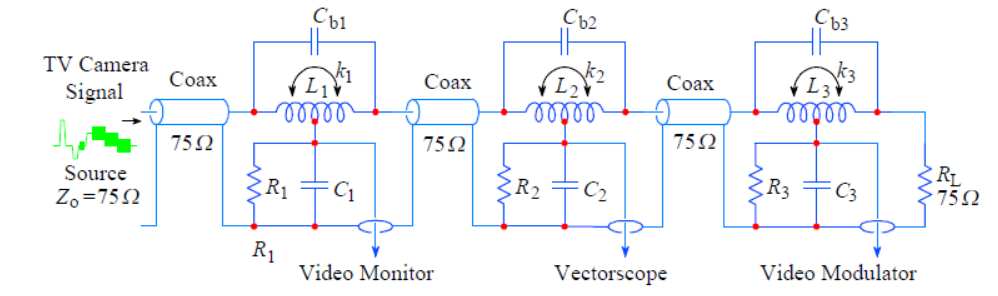
传输线线路多点端接

小程序实现

小程序可以计算以上讨论的所有T-Coil类型，如下所示：

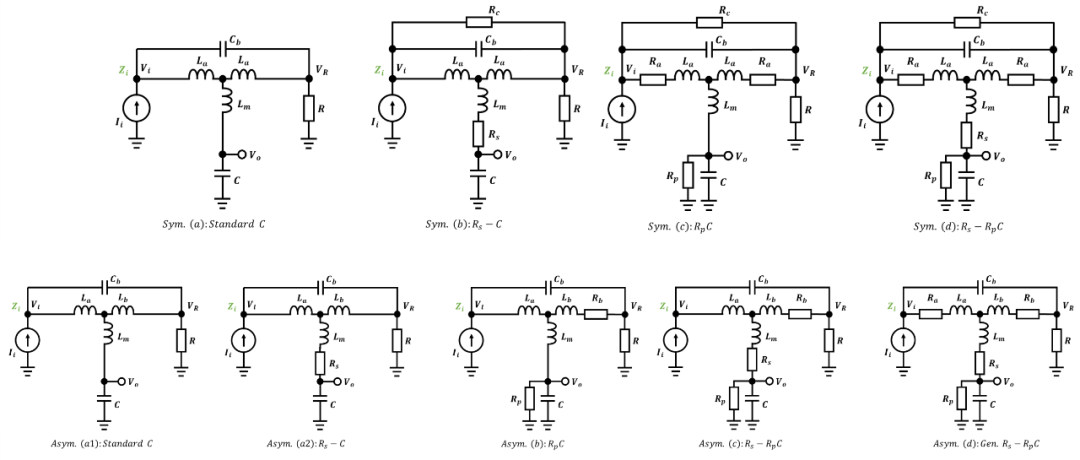
其中的Asym.(a1)是依据来最大化带宽的非对称T-Coil设计原理图，其他类型和BOB ROSS的一致，如下例子为BOB ROSS的计算表格验证：

对于对称T-Coil (d)，输入、、、，计算结果如下：

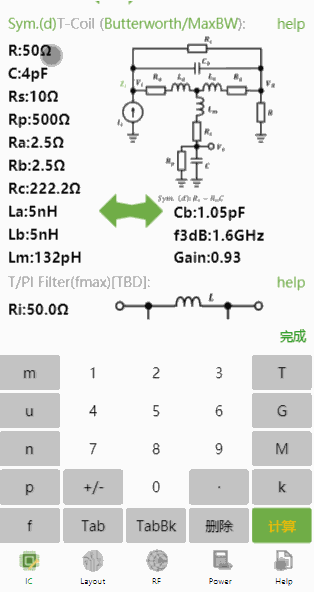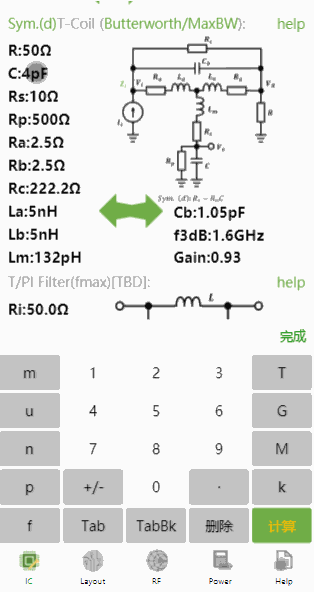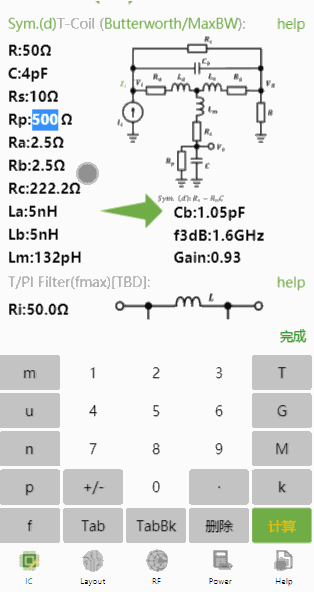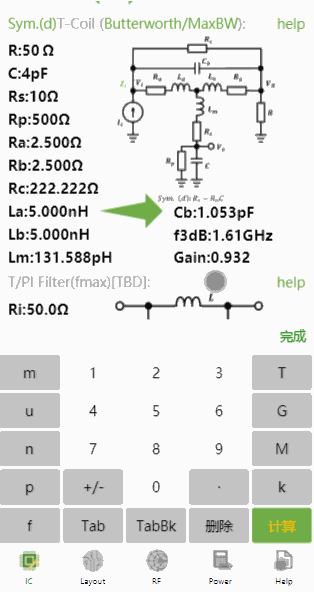
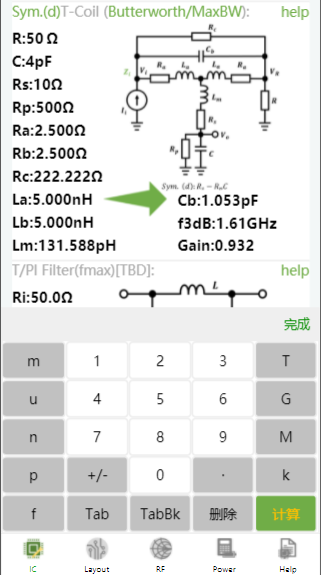
同样的参数，并且设置，使用非对称T-Coil设计，结果如下：

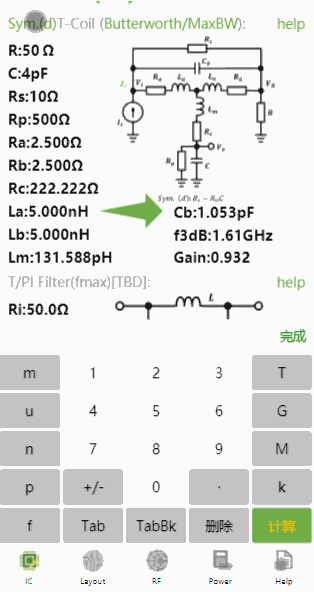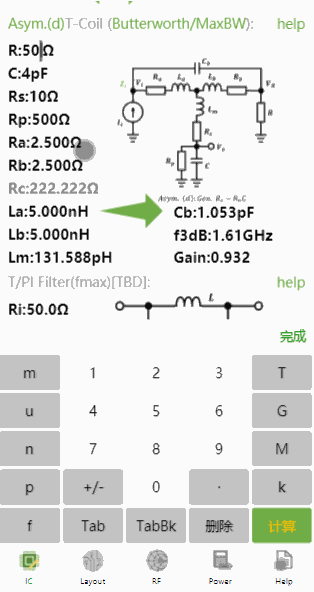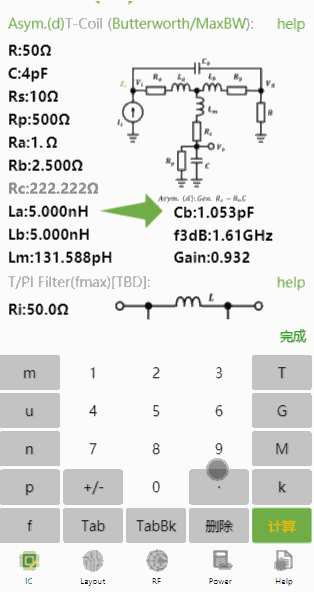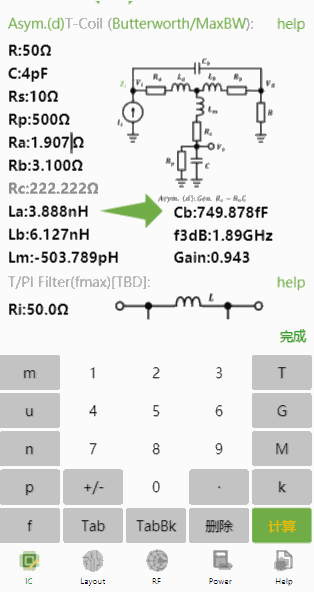
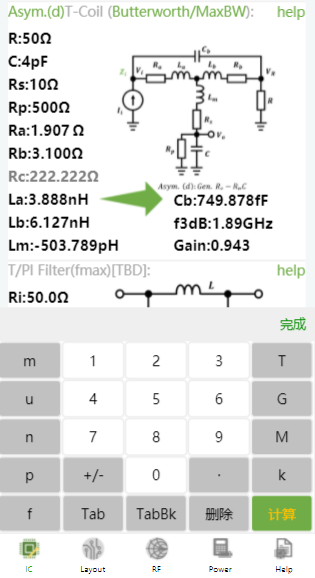
小程序中除了可以正向设计T-Coil，还可以依据带宽反推电容，比如带宽到10GHz，电容的最大值为多少？

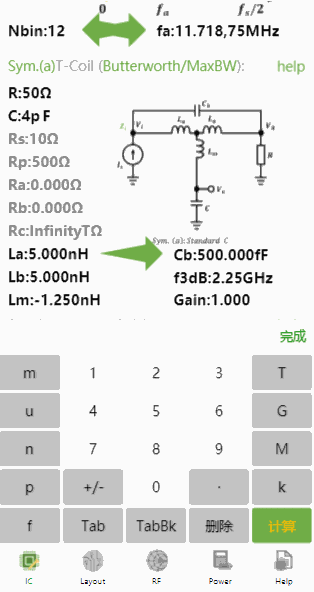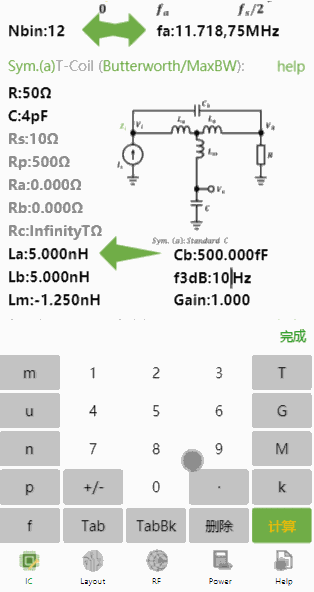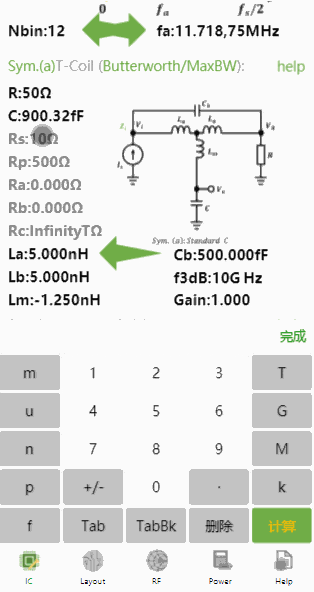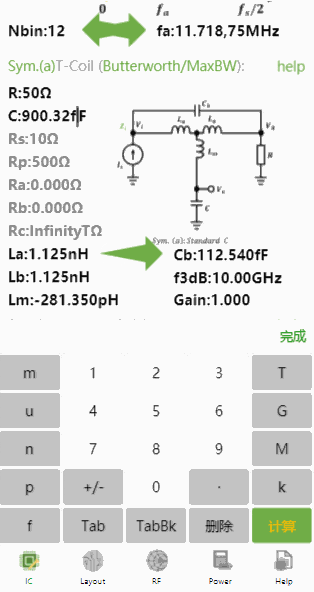
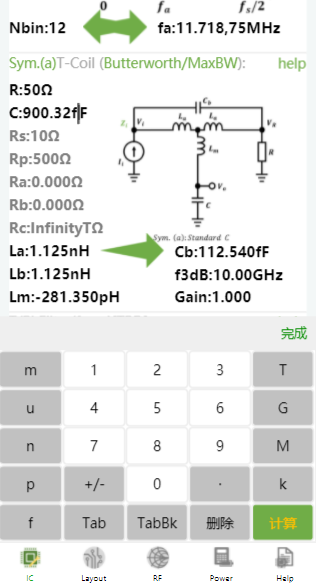
得到最终，这是最能实现10GHz带宽的最大值了。

若需要体验小程序，请点击如下图片链接(软件更新有滞后)：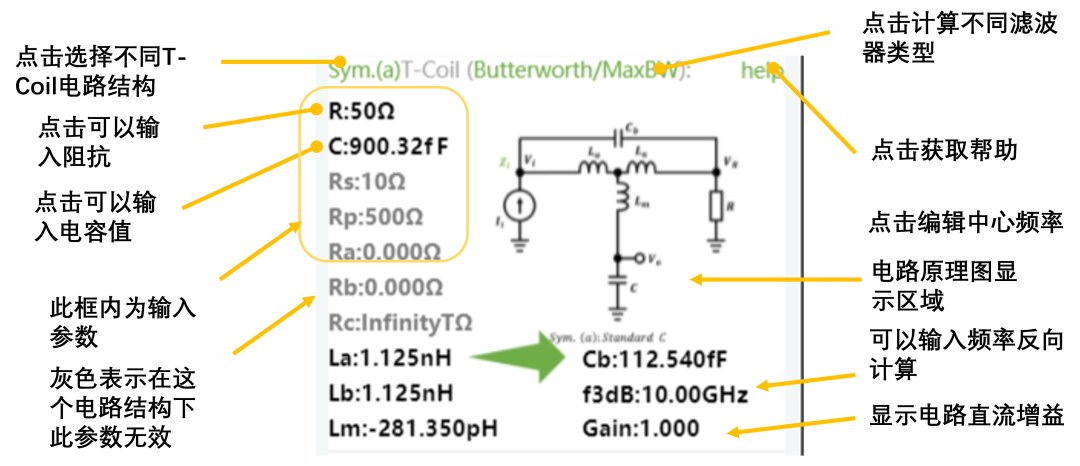

审核编辑：汤梓红