分为三大主要内容:
一、拓扑参数计算
二、开环和单、双闭环M文件配置及仿真
三、Tunner工具仿真双闭环
1.1 Buck拓扑关键参数计算

1.2 闭环仿真验证Buck参数指标

输出电压纹波在1.6V以内,设置输出电容合理

电感纹波接近8A,设置输出电感合理

2.1 开环模型

仿真结果:较大的过冲,可以使用M文件运行看搭建开环模型是否接近合理。

L=0.0004;
r=0;
C=0.000047;
R=4;
VIN=320;
Vout=80;
Ts=1/20000;
D=0.25;
s=tf('s');%传递函数变量
%主函数对应的开环传递函数
Hs=1/(L*C*s^2+L/R*s+r*(C*s+1/R)+1);
% bode(Hs);
% hold on
step(Hs*80,0.05) %观察主电路开环阶跃响应;Hs*80等于此电路输出电压,运行0.05s

主电路开环阶跃响应如上所示,说明开环模型输入数值正确,开环模型搭建完成,仿真器步长选择合理(目前选择的寄生参数,影响较小),进入下一步操作;
M文件代码如下
%% PI控制器
Voltage_ki=35; %引入PI控制器,无法抑制波特图震荡凸起的尖峰(闭环传递),尖峰依旧存在,反映仿真时,输出过冲严重;穿越频率不是-20db,相位裕度也较小。
Voltage_kp=10; %只引入积分控制,输出电压波动无法抑制,积分器滤波输出电压波动,无法反馈
G_voltage_pi=Voltage_ki/s+Voltage_kp; %kp增大观察波形,输出震荡严重,最后选用0.2
G_voltage_open=G_voltage_pi*Hs;
% bode(G_voltage_open);
% hold on
% bode(G_voltage_open/(1+G_voltage_open));
试揍调节PI参数,当P等于35,I等于10时,观察波特图如下所示,系统整体开环传递函数G_voltage_open 带宽接近4K,相位裕度接近10°左右,系统很不稳定,运行此参数的输出电压仿真波形如下:

运行此参数的输出电压仿真波形如下:虽然输出电压响应速度很快,由于带宽较大,相位裕度很差,穿越频率呈现-2斜率(这里的PI控制器只能缓冲PI初始极点的影响,主功率LC双重极点还是没法补偿)

继续调节PI参数,当P等于35,I等于1时,可以看到,输出电压速度200m左右才达到稳定,这里还没有做动态,不言而喻,做动态肯定差;

一开始的地方出现震荡,主要还是闭环传递函数波特图在穿越频率处尖峰的影响,波特图如下所示,如右边第二个橙色波形。当P等于35,I等于0.3时,带宽明显较低,如标识的角频率和相位裕度。再次对此参数代入PI控制器,输出电压波形如下所示:可以看到,输出开启尖峰明显减小。也可以改变I参数试试效果


上节说到的PI控制器补偿,其实用于Buck电路中,是微乎其微的,这里只是做一个简单的PI控制讲述,数字PI参数对波形的影响效果;接着上一节,讲述PID控制器补偿
2.3单电压环 PID控制器补偿仿真
模型如下所示

M文件调试代码如下
%% 使用PID控制器调节 没有考虑到输出电容的ESR情况下,属于二型补偿网络,下面的PID形式只有两个零点
k=140; %先定k值,k值影响穿越频率,穿越频率设置在开关频率的1/10处,再调节T1,T2;
T1=1/100;
T2=1/10000; %T1,T2的值,可以先观察主电路的振荡凸起的波形的频率位置,再选择放置T2;T2放置在凸起频率右侧,穿越频率-20db穿越,波特图可以对比
G_voltage_kp=k*T1*(1+T2/T1);
G_voltage_ki=k*T1/T1;
G_voltage_kd=k*T1*T2; %根据T1,T2,k值配置后,计算出PID参数,代入模型中
G_voltage_pid=k*(1+T1*s)*(T2*s+1)/s; %只有两个零点,一个积分器
bode(G_voltage_pid*Hs);
hold on
bode(G_voltage_pid);
hold on
% bode(G_voltage_pid*Hs/1+G_voltage_pid*Hs);
这里的穿越调试在2K左右,如下波特图所示,由于这边的PID只有两个零点,一个零点缓冲了初始极点的影响,另一个零点补在了主功率双极点的右侧,抵消了一个极点的影响,剩下-1斜率穿越;(零极点配置法,如果要考虑输出电容ESR的影响,PID需要加上极点),如我配置的另一个案例,可以多加一两个极点,当然,高频极点越多越好;配置完后,可以按照上例,M文件自动导出封装好的PID参数(变量最好放在变量工作区,方便浏览),再代入数字PID控制器;需要提到一点,如果考虑输出电容ESR的影响,主功率原始系统开环传递函数需要在分子上加一个零点;再作为级联传递函数的一部分,再进行波特图补偿。
T1=1/1884; %放置一个零点在双重极点的角频率位置的1/2处,缓冲PI控制器极点对系统的不利影响
T2=1/3768; %T2零点放置在LC双重极点的0.8~1之间,穿越频率-20db穿越,波特图可以对比
T3=1/(2*pi*fc);
G_voltage_pid=k*(1+T1*s)*(T2*s+1)/(s*(1+T3*s));
实际补偿中,只使用一个零点和极点的控制器,最多只能实现在穿越频率处相位裕度拉高90°(零点和极点位置距离很远才能实现);使用两个极点和零点补偿能拉升180°相位,操作较为灵活。

运行该参数的实际效果:可以看到,相比PI补偿器,PID补偿后的响应速度加快;

2.4 单电流环补偿仿真
单电流环模型如下所示

M代码如下所示
current_kp=3;
current_ki=90;
k3=0 %当k等于0时,开环比闭环传递函数的带宽变低,可以观察闭环波特图
G_current_pi=current_kp+current_ki/s;
Gs_current=G_current_pi/(L*s+r); %不考虑输出电压扰动,输出电压前馈,k值等于1时
Gs_current1=G_current_pi*(R*C*s+1)/((R*C*s+1)*(L*s+r)+(1-k3)*R); %k值不等于1时
bode(Gs_current);
hold on
bode(Gs_current1);
hold on
bode(Gs_current/(Gs_current+1));
bode(Gs_current1/(Gs_current1+1));
可以看到,输出电压在2ms内已经达到稳定,响应很快(加入输出电压前馈)
分析对比加入电压全前馈和不加前馈波特图对比

由上面波特图可以发现,不带电压前馈的闭环传递函数,在低频段已经出现小于0db的情况,说明了不带电压前馈功能的带宽速度很低,待会仿真看看输出电压效果既可以,如下图所示:需要经过很长时间才能达到稳定状态

2.5 电流电压双闭环控制
控制模型如下所示

输出电压仿真结果如下所示:输出电压在10ms内达到稳定,输出无静差

来看下外环电压环的带宽情况,观察波特图:可以看到,外环电压环带宽其实很低,才100Hz左右,但是输出看出来,好像还不错,其原因在于其拥有内环(电流环),双环控制,能采集更多的信息;快速性方面还得观察动态响应波形

来观察的双闭环下的动态响应波形,负载在10A~20A之间跳变,如下所示

可以看到,动态响应,输出虽然没有阻尼震荡的现象(不带电压前馈),但过冲和恢复时间较差,特别是过冲,根本原因主要在于输出电容取值较小和闭环PI参数设置还得继续优化(带宽/电压环和电流环的跟踪性)。
3.1 整定电流环

3.2 整定电压外环
先把电流内环的PI参数整定出来,和前面的零极点配置法进行对比,电流内环整定后,输出电压尽量不要小震荡,会影响整个系统的动态响应波形。电流环整定后,作为整个系统的内环,再进行整定电压环。

整定后的输出电压动态响应波形(还可以继续优化)

3.3 tunner工具整定中,简要说明

其中电流环整定中,模型辨识Structure这里要选择一阶系统,电压外环整定中,选定二阶阻尼震荡系统,外加一个零点(ESR)
-
matlab
+关注
关注
185文章
2980浏览量
230888 -
BUCK
+关注
关注
32文章
483浏览量
64353 -
变换器
+关注
关注
17文章
2109浏览量
109496 -
闭环仿真
+关注
关注
0文章
3浏览量
4323
发布评论请先 登录
相关推荐
单级BUCK-BOOST变换器实现APFC的原理及分析
buck级联推挽变换器小信号建模的问题
ZCS-PWM Buck变换器的工作原理是什么?
DCM_Buck_Boost变换器的建模与控制设计讲解
buck变换器介绍_buck变换器matlab仿真
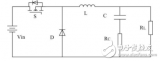
buck变换器设计_自制buck变换器
使用PSpice进行Buck变换器的仿真研究的资料说明
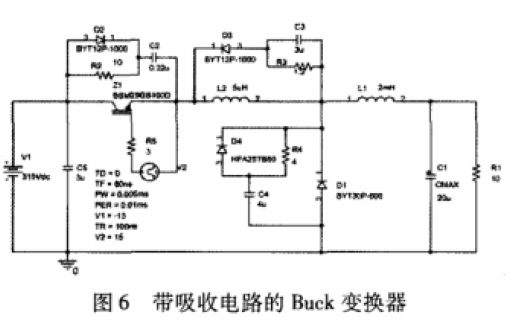
如何在Buck DCDC变换器输出电压纹波是进行仿真研究的资料说明
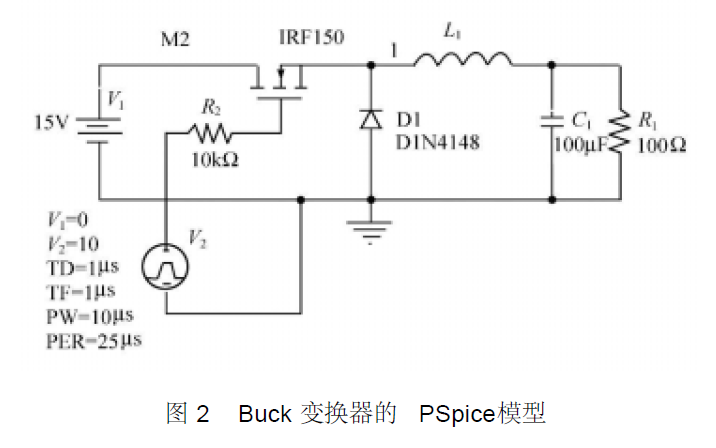
Buck变换器的工作原理与设计的学习课件免费下载
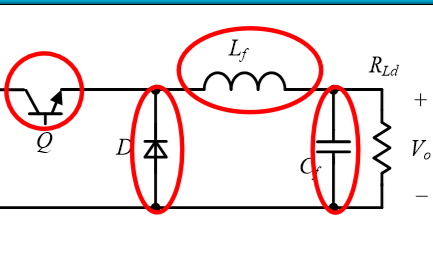




 基于Buck变换器Matlab闭环仿真
基于Buck变换器Matlab闭环仿真










评论