基于半桥LLC谐振变换器Mathcad和Matlab小信号建模分析

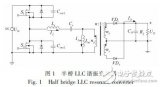
基于扩展描述函数法和Simplis时域仿真法进行半桥LLC变换器小信号分析

扩展描述函数法：列出状态方程，对状态变量进行傅里叶分解，得到线性状态方程（依据谐波平衡原理），求解稳态参数解；接着在大信号模型方程中，引入小信号扰动，并进行稳态分量和扰动量分离；根据系统的小信号模型，推导状态空间方程，再把状态空间方程转换成传递函数矩阵形式，进行波特图分析和双闭环控制。

Simplis时域仿真法：采用分段线性建模（仿真速度加快），对控制端施加小信号扰动，测试输出电压小信号，扫频得到频域特性曲线；缺点：不能获得系统的小信号数学模型，不理解底层，也就不便于学习。

一、半桥LLC设计参数

Vin_min=360;
Vin_nom=400;
Vin_max=420;
Vout=25;
Po=200;
Cr=27.1*10^(-9);
Lr=64.8*10^(-6);
Lm=462.9*10^(-6);
Co=2200*10^(-6); 
rc=0.005;   %滤波电容等效电阻
rs=0.005;    %谐振电感电容串联电阻

二、扩展描述函数法

得出稳态解

上图中，已经使用了以矩阵形式表示稳态方程组；其中Uo为输入变量稳态矩阵，Y为状态变量稳态矩阵；得出状态变量稳态解：如下所示

其中，上述ILrs、Vcrs、ILms分别为谐振电感电流、谐振电容电压和励磁电感电流的正弦分量，ILrc、Vcrc、ILmc分别为谐振电感电流、谐振电容电压和励磁电感电流的余弦分量；

半桥LLC谐振变换器小信号模型如下所示（状态空间表达式）

其中，x为状态变量，u为输入变量，y为输出变量，

A、B、C、D为系数矩阵如下所示

进一步，拉氏变换，如下所示

接着，利用Matlab软件进行绘制变换器控制到输出电压的开环传递函数：

G2=ss(A1,B1,C1,D1);
G_LLC_open=tf(G2);
bode(G_LLC_open);
hold on

由波特图可知，相频曲线的初始相位为180°，相当于一个反向器，因而输出电压反馈采用正反馈控制策略；

当然，如需获得变换器电流环的数学模型，只需要将输出变量设置成输出电流Io,其余矩阵参数保持不变即可得到电流环的数学模型，这里不多做解释；

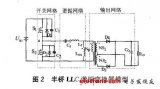
三、Simplis时域仿真法

半桥LLC开环模型如下：

先进行Transient瞬态分析，再进行AC分析；界面如下所示

Vin=400V,输出满载，波特图如下所示：

由上面扩展描述函数法和Simplis时域仿真法可知，使用扩展描述函数法进行建模具有较好的准确性。

单环/双闭环matlab仿真，mathcad零极点配置/Matlab sisotool工具零极点配置法下节再讲吧.....