3.12 MATLAB信道编码例子
在本节中,我们将使用一种教学方法和一系列MATLAB程序,检查工具箱在信道编码方面提供的内容。首先,我们将建立一个系统,使用卷积编码和基于硬判决解码的维特比译码。然后,我们将使用软判决译码更新算法。最后,我们将用卷积编码算法代替卷积编码,并比较每个阶段的性能。通过这些简单的练习,我们不仅将了解使用MATLAB和通信系统工具箱为移动通信模型增加更多复杂性是多么容易,而且我们将清楚地看到,BER性能的显著提高解释了turbo编码在LTE标准的信道编码中所起的重要作用。
3.12.1 误差校正与检测
信道编码包括错误检测和纠错。通过使用CRC(循环冗余校验)检测器进行错误检测,接收器可以请求传输的重复,这被称为自动重复请求。前向纠错编码允许基于传输信号中包括的冗余比特来校正错误。错误检测和前向纠错的混合称为HARQ(Hybrid Automatic Repeat Request,混合自动重复请求)构成了大多数3G标准的组成部分,并且也被用于LTE标准。纠错码通常分为分组码和卷积码。卷积码在2G和3G移动通信标准中有着广泛的应用,主要是因为其复杂度较低。
在这一节中,我们将详细说明我们已经增长的Matlab模型,它已经包含了调制,包括信道编码。作为解释在LTE标准中使用turbo编码的价值和动机的完美工具,我们将比较卷积编码和turbo编码的性能。此外,为了解释在使用接收机设计中所涉及的折衷,我们将比较具有和不带软判决译码的调制编码组合的性能。
3.12.2 卷积码
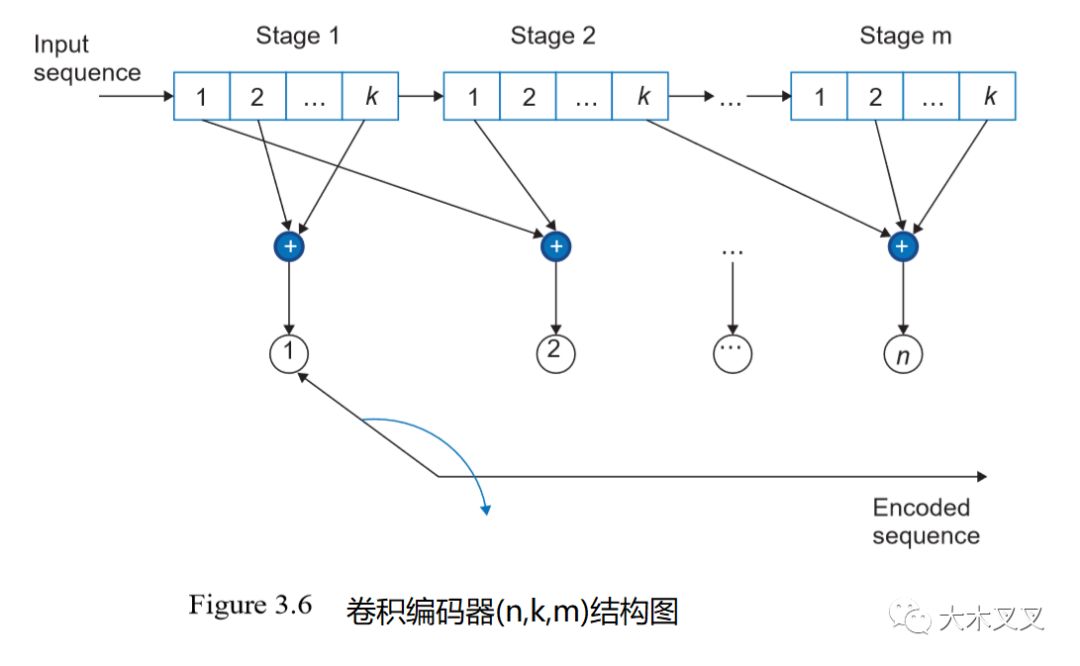
卷积码是由输入序列与编码器的脉冲响应卷积而产生的。编码器接受k位输入样本块,并通过对当前数据块和m个先前输入块进行操作,产生n位输出样本块。编码器的编码速率由比Rc=k/n给出,卷积编码器由这三个参数(n,k,m)指定。图3.6示出了卷积编码器。
3.12.3 硬判决Viterbi译码
在本练习的第一次迭代中,我们修改了上一节中的MATLAB函数,以在调制中添加信道编码方案。当使用信道编码方案时,发射机通过无线信道发送冗余比特和消息比特。接收机接收发送的信号,并使用冗余位来检测和校正信道引入的一些错误。让我们开始向通信系统添加卷积编码器和维特比解码器。该通信系统使用硬判决维特比译码,其中解调器将接收信号映射到位,然后将位传递到维特比译码器进行纠错。下面的MATLAB函数(chap3_ex03_qpsk_viterbi)使用QPSK调制和AWGN信道的硬判决Viterbi解码。
1function [ ber,bits ] = chap3_ex03_qpsk_viterbi( EbNo,maxNumErrs,maxNumBits )
2%% Initializations
3
4persistent Modulator AWGN DeModulator BitError ConvEncoder Viterbi
5
6if isempty(Modulator)
7 Modulator = comm.QPSKModulator('BitInput',true);
8 AWGN = comm.AWGNChannel;
9 DeModulator = comm.QPSKDemodulator('BitOutput',true);
10 BitError = comm.ErrorRate;
11 ConvEncoder = comm.ConvolutionalEncoder('TerminationMethod','Terminated');
12 Viterbi = comm.ViterbiDecoder('InputFormat','Hard','TerminationMethod','Terminated');
13end
14%% Constants
15FRM = 2048;
16M = 4;
17k = log2(M);
18codeRate = 1/2;
19snr = EbNo + 10*log10(k)+10*log10(codeRate);
20AWGN.EbNo = snr;
21
22%% Processing loop modeling transmitter, channel model and receiver
23numErrs = 0;
24numBits = 0;
25results = zeros(3,1);
26while((numErrs< maxNumErrs)&&(numBits< maxNumBits))
27 % Transmitter
28 u = randi([0 1],FRM,1);
29 encoded = ConvEncoder.step(u);
30 mod_sig = Modulator.step(encoded);
31
32 % Channel
33 rx_sig = AWGN.step(mod_sig);
34
35 % Receiver
36 demod = DeModulator.step(rx_sig);
37 decoded = Viterbi.step(demod);
38 y = decoded(1:FRM);
39 results = BitError.step(u,y);
40 numErrs = results(2);
41 numBits = results(3);
42end
43
44%% Clean up & collect results
45ber = results(1);
46bits = results(3);
47reset(BitError);
48
49end
通过在BERTool中运行该函数,我们可以测量硬判决维特比译码的性能,并与上限理论结果进行比较。检查图3.7中的结果,我们可以看到模拟的BER曲线低于理论上限值,这与我们的期望是一致的。这些结果表明,为了达到更好的性能,我们需要改进我们的解码算法。
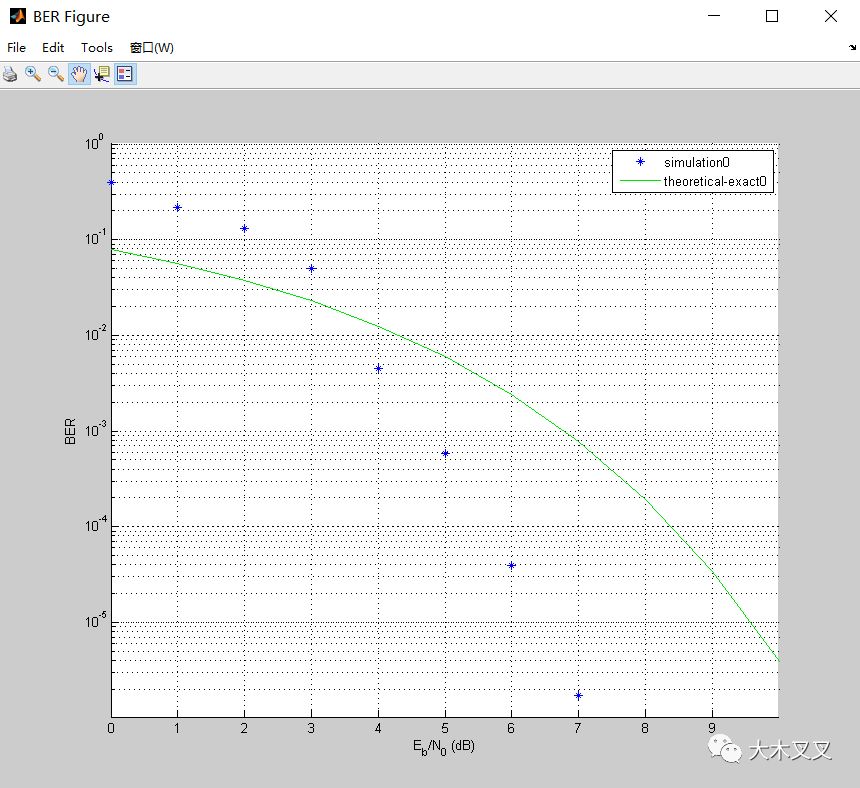
图3.7 Viterbi译码的性能和AWGN信道的QPSK调制对比
3.12.4 软判决Viterbi译码
在这个迭代中,我们通过使用软判决译码算法来改进BER性能结果。在软判决译码中,解调器将接收到的信号映射到对数似然比。这些概率度量是基于接收到正确数据的可能性的对数而不是损坏的数据。当提供对数似然比作为对维特比解码器的输入时,解码器的误码率性能得到改善。通过改变几个解调器和维特比译码器系统目标参数,可以得到一种实现软判决维特比译码的算法。下面的MATLAB函数(chap3_ex04_qpsk_viterbi_soft() )已被更新为使用软判决维特比译码。
1function [ ber,bits ] = chap3_ex04_qpsk_viterbi_soft( EbNo,maxNumErrs,maxNumBits )
2%% Initializations
3
4persistent Modulator AWGN DeModulator BitError ConvEncoder Viterbi Quantizer
5
6if isempty(Modulator)
7 Modulator = comm.QPSKModulator('BitInput',true);
8 AWGN = comm.AWGNChannel;
9 DeModulator = comm.QPSKDemodulator('BitOutput',true,'DecisionMethod','Log-likelihood ratio','VarianceSource','Input port');
10 BitError = comm.ErrorRate;
11 ConvEncoder = comm.ConvolutionalEncoder('TerminationMethod','Terminated');
12 Viterbi = comm.ViterbiDecoder('InputFormat','Soft','SoftInputWordLength',4,'OutputDataType','double','TerminationMethod','Terminated');
13 Quantizer = dsp.ScalarQuantizerEncoder('Partitioning','Unbounded','BoundaryPoints',-7:7,'OutputIndexDataType','uint8');
14
15
16end
17%% Constants
18FRM = 2048;
19M = 4;
20k = log2(M);
21codeRate = 1/2;
22snr = EbNo + 10*log10(k)+10*log10(codeRate);
23noise_var = 10.^(-snr/10);
24AWGN.EbNo = snr;
25
26%% Processing loop modeling transmitter, channel model and receiver
27numErrs = 0;
28numBits = 0;
29results = zeros(3,1);
30while((numErrs< maxNumErrs)&&(numBits< maxNumBits))
31 % Transmitter
32 u = randi([0 1],FRM,1);
33 encoded = ConvEncoder.step(u);
34 mod_sig = Modulator.step(encoded);
35
36 % Channel
37 rx_sig = AWGN.step(mod_sig);
38
39 % Receiver
40 demod = DeModulator.step(rx_sig,noise_var);
41 llr = Quantizer.step(-demod);
42 decoded = Viterbi.step(llr);
43 y = decoded(1:FRM);
44 results = BitError.step(u,y);
45 numErrs = results(2);
46 numBits = results(3);
47end
48
49%% Clean up & collect results
50ber = results(1);
51bits = results(3);
52reset(BitError);
53
54end
理论上,我们预期结果会有2dB的改进,这正是图3.8中所示的模拟曲线。接下来,我们检查Turbo编码,看看它是否可以提供任何改进的BER结果。
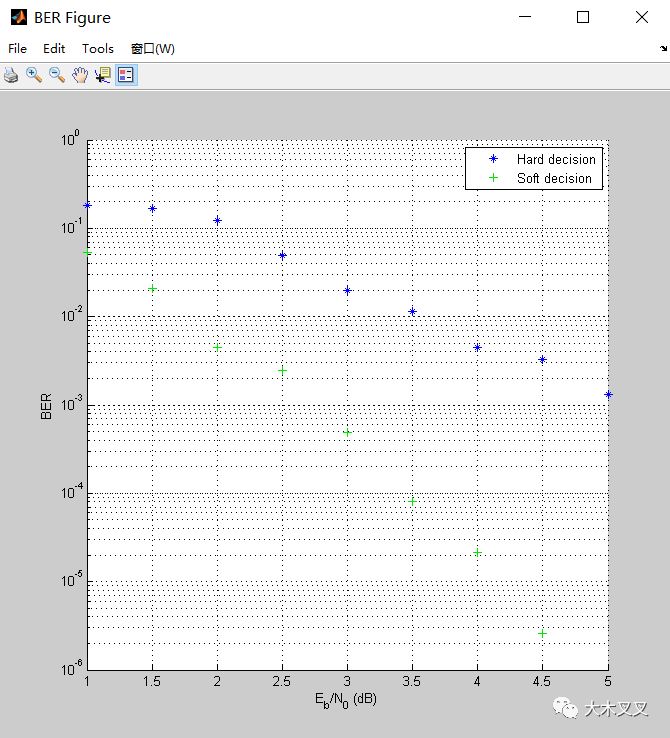
图3.8 硬判决Viterbi译码 Vs 软判决Viterbi译码
3.12.5 Turbo 编码
Turbo码大大提高了软判决Viterbi译码的误码率性能。Turbo编码在发射机处并行使用两个卷积编码器,在接收机处串联使用两个A后验概率(APP)解码器。此示例使用率1/3 turbo编码器。对于每个输入位,输出具有一个系统位和两个奇偶位,总共三位。
下面的MATLAB函数已被更新,使用Turbo编码器和解码器。注意,Turbo解码是一个迭代迭代,性能随着迭代次数的增加而提高。在这个例子中,我们选择了六作为解码器执行的迭代次数。
1function [ ber,bits ] = chap3_ex05_qpsk_turbo( EbNo,maxNumErrs,maxNumBits )
2%% Constants
3FRM = 2048;
4Trellis = poly2trellis(4,[13 15],13);
5Indices = randperm(FRM);
6M = 4;
7k = log2(M);
8R = FRM/(3*FRM+4*3);
9
10snr = EbNo + 10*log10(k)+10*log10(R);
11noise_var = 10.^(-snr/10);
12
13%% Initializations
14persistent Modulator AWGN DeModulator BitError TurboEncoder TurboDecoder
15
16if isempty(Modulator)
17 Modulator = comm.QPSKModulator('BitInput',true);
18 AWGN = comm.AWGNChannel;
19 DeModulator = comm.QPSKDemodulator('BitOutput',true,'DecisionMethod','Log-likelihood ratio','VarianceSource','Input port');
20 BitError = comm.ErrorRate;
21 TurboEncoder = comm.TurboEncoder('TrellisStructure',Trellis,'InterleaverIndices',Indices);
22 TurboDecoder = comm.TurboDecoder('TrellisStructure',Trellis,'InterleaverIndices',Indices,'NumIterations',6);
23end
24
25
26%% Processing loop modeling transmitter, channel model and receiver
27AWGN.EbNo = snr;
28numErrs = 0;
29numBits = 0;
30results = zeros(3,1);
31while((numErrs< maxNumErrs)&&(numBits< maxNumBits))
32 % Transmitter
33 u = randi([0 1],FRM,1);
34 encoded = TurboEncoder.step(u);
35 mod_sig = Modulator.step(encoded);
36
37 % Channel
38 rx_sig = AWGN.step(mod_sig);
39
40 % Receiver
41 demod = DeModulator.step(rx_sig,noise_var);
42
43 decoded = TurboDecoder.step(-demod);
44 y = decoded(1:FRM);
45 results = BitError.step(u,y);
46 numErrs = results(2);
47 numBits = results(3);
48end
49
50%% Clean up & collect results
51ber = results(1);
52bits = results(3);
53reset(BitError);
54
55end
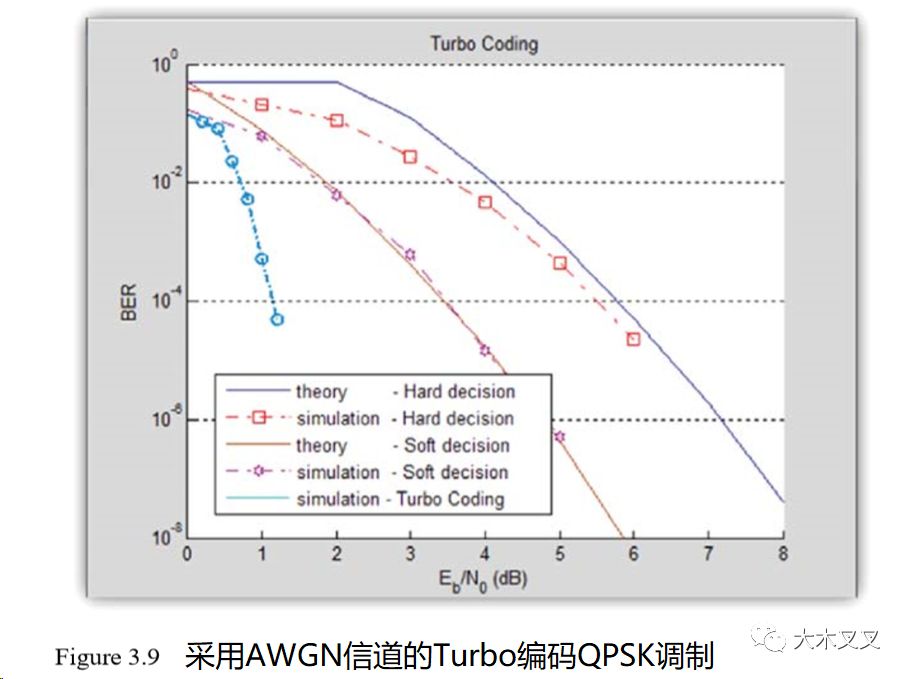
图3.9示出了在AWGN信道下QPSK调制中turbo编码的结果。注意,在1dB,我们有一个BER值发生在5dB的硬判决和3dB软判决解码。这清楚地表明了Turbo编码算法的优越性。记住,这种性能增益是以计算复杂性的增加为代价的 (我的电脑单单计算 Turbo Coding 就花费了很长时间,而我的电脑配置是最新的 CORE i7)。我们的Turbo解码器经过六次迭代译码以达到这一性能。我们将在Turbo译码器中研究性能和复杂性之间的折衷。
3.13 本章总结
Simulink及其工具箱提供了用于建模、仿真、评估性能、以及最终生成和实现通信系统代码的能力。对于建模和仿真,我们可以使用来自通信系统工具箱的算法构建块,作为系统对象或Simulink块。在MATLAB中可以更有效地对移动标准的PHY处理的许多方面进行建模和仿真,因为我们可以专注于将更高级的功能引入系统模型,而不是创建诸如调制器和编码器之类的构建块。特别感兴趣的是通信系统工具箱的系统对象。系统对象是为基于块的流系统的建模而设计的自文档化、易于使用和定制的建模和仿真组件。
当模拟复杂系统时,我们需要访问各种加速技术。这些技术帮助我们处理更多的测试数据,并在合理的模拟时间内获得统计上正确的评估。MATLAB工具箱,如并行处理工具箱和MATLAB编码器可以加快仿真。最后,为了在软件或硬件上实现设计,我们可以使用代码生成产品通过自动C或HDL代码生成来获得对精确实现细节的访问。
-
解调器
+关注
关注
0文章
286浏览量
25812 -
MATLAB仿真
+关注
关注
4文章
176浏览量
19922 -
QPSK调制
+关注
关注
0文章
11浏览量
7619 -
CRC效验
+关注
关注
0文章
30浏览量
1102 -
卷积编码器
+关注
关注
0文章
6浏览量
2434
发布评论请先 登录
相关推荐
FPGA基础学习笔记--组合逻辑电路-编码器和译码器
大围数QC_LDPC码的译码器该怎么设计?
编码器和译码器(数电实验报告)精选资料分享
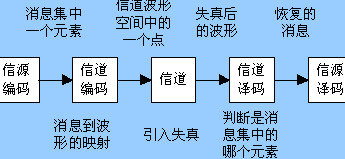
信道编码——引言
基于FPGA的数字音频广播信道编码器的实现
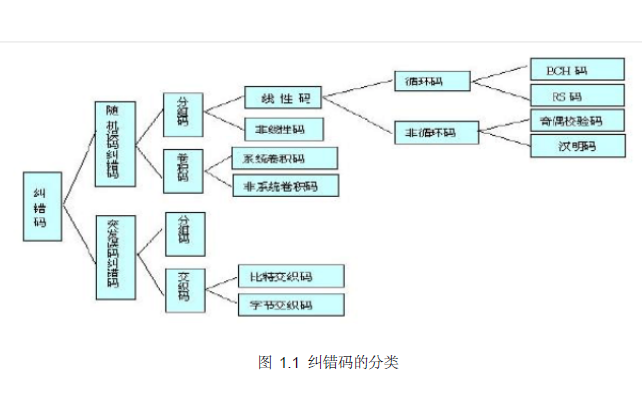
如何使用FPGA实现信道编码




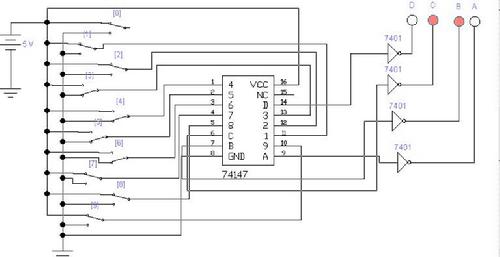
 信道编码器与译码器原理仿真
信道编码器与译码器原理仿真










评论