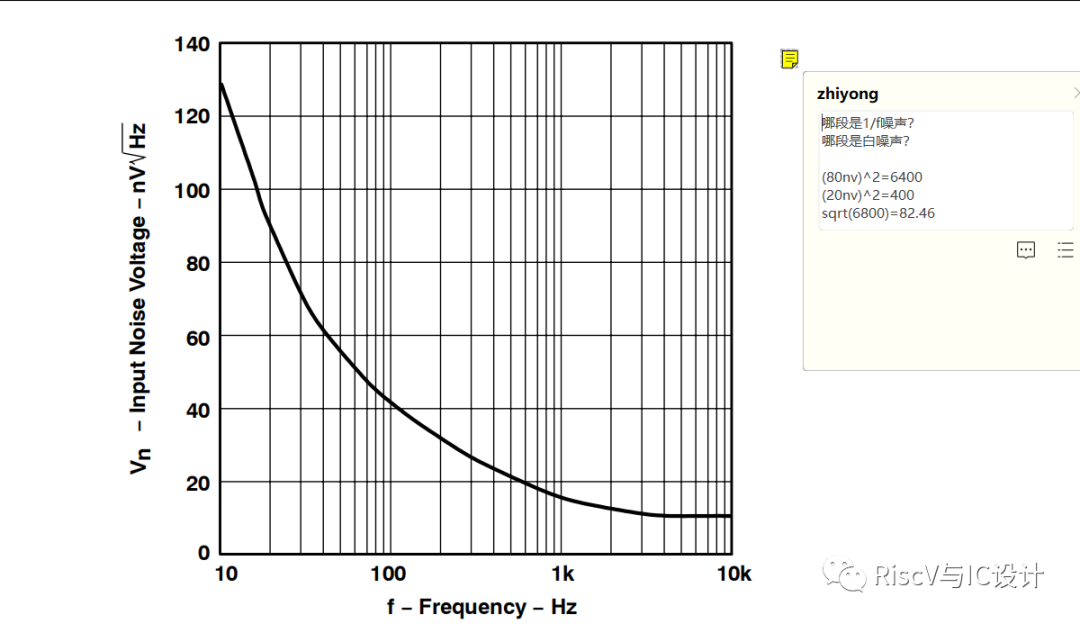
这是一个典型的运放芯片的等效输入噪声功率谱密度曲线,其低频以1/f噪声为主,随频率增加而快速下降,中高频段基本为直线,以白噪声为主,前述讲的电子系统5种噪声:散粒噪声、热噪声都是白噪声,闪烁(变)噪声即1/f噪声,而突发噪声和雪崩噪声在放大器设计里由于芯片工艺的进步,这两类已经很小了,可以不考虑,可见放大器芯片的散粒噪声、热噪声都是白噪声,闪烁(变)噪声即1/f噪声刚好符合上图 的实际测试数据,我们把运放的噪声分为两类:白噪声(包括散粒噪声、热噪声)和1/f噪声,则总噪声为

这是在特定带宽内的噪声功率,计算的关键是求出C和k^2,
而现在我们有的只是运放数据手册上的一张噪声功率谱密度曲线,如何从此曲线上求C和k^2?我们先做一个数字游戏:
(2)^2+( 3 )^2=4+9=13=( **3.6** )^2
(2)^2+( 5 )^2=4+25=29=( **5.39** )^2
(2)^2+( 7 )^2=4+49=53=( **7.28** )^2
(2)^2+( 10 )^2=4+100=104=( **10.2** )^2
(2)^2+( 20 )^2=4+400=404=( **20.01** )^2
大家发现了什么规律?一个大噪声与一个小噪声叠加时,当差别较大时,总的输出就基本等于大噪声,小噪声的影响可以忽略!
那么C如何求?当频率很高时,1/f噪声衰减的已经可以忽略,而白噪声的频谱一直保持常数,所以大家厂家提供的噪声功率谱曲线时,远离低频的密度数值就是C!前图的C在10khz基本上12nv/根号HZ,现在如何求k^2 ?这里介绍一个常用的方法:
先选一个足够低的频率,比如上图的10hz,对应曲线显示130nv/根号Hz,此点的噪声包括了白噪声与1/f噪声,白噪声的C前面已经求得12nv,

现在有了C和k^2,就可以求出设计频率范围内的运放输入噪声的有效值了。
有时我们不直接求k^2,定义一个转折频率fnc:

-
放大器
+关注
关注
143文章
13612浏览量
213773 -
衰减器
+关注
关注
4文章
640浏览量
34384 -
运放芯片
+关注
关注
0文章
21浏览量
19518 -
白噪声
+关注
关注
0文章
14浏览量
10493 -
热噪声
+关注
关注
0文章
46浏览量
8174
发布评论请先 登录
相关推荐
放大器噪声的来源

低噪声放大器,低噪声放大器型号参数
低噪声设计与最佳放大器选择
放大器的噪声




 放大器的噪声问题(2)
放大器的噪声问题(2)












评论