消除前馈通道的Miller补偿：电流跟随器结构

常规Miller补偿结构，将Cc跨接在M2的G、D之间，会引入一条前馈通路，从而引入一个RHP（右半平面）的零点。

RHP零点对稳定性伤害极大，体现在2个方面：（1）增益：+20dB/10倍频（和极点的影响相反）；（2）相位：和左半平面极点一样，会提供相位延迟。

如何消除（减弱）RHP零点的影响呢？大致有以下几种方法：

（1）引入调零电阻Rz=1/gm2，可以将RHP零点推到无穷远

（2）进一步增大调零电阻Rz，使其>1/gm2，从而将RHP零点变成LHP零点，LHP零点对稳定性有补偿作用，甚至可以用于抵消次极点P2

（3）引入额外的电路打断前馈通路，有电压跟随和电流跟随两种方式。

本文研究的就是上述3种方法中的第3条，采用“电流跟随”的方式打断Cc的前馈通路。

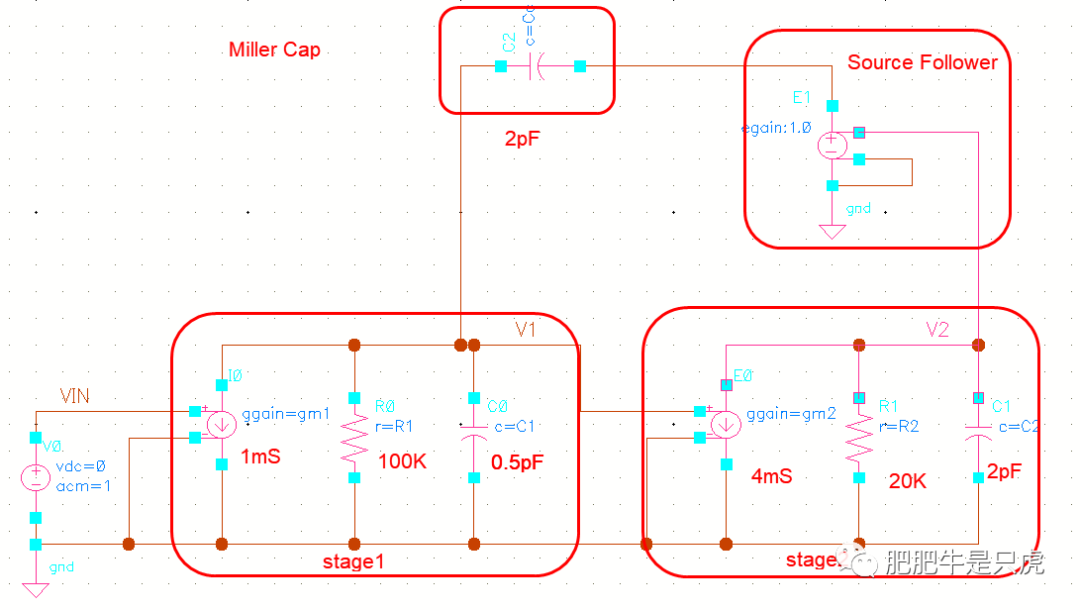
小信号图如下：

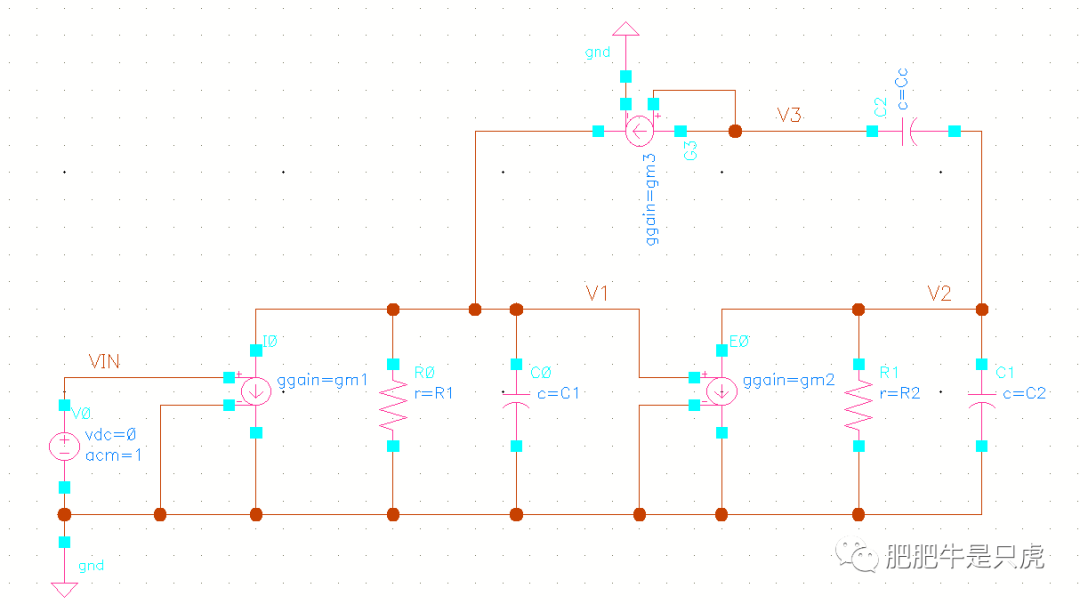
**用matlab的符号运算推导传函，**程序如下：

%%

clear;clc;

syms Vin gm1 gm2 gm3 R1 R2 R3 C1 C2 C3 Cc V1 V2 V3 positive;

syms s ;

%

eq1 = sym('gm1Vin + V1/R1 + V1sC1 - gm3V3 = 0');

eq2 = sym('gm2V1 + V2/R2 + V2s*C2 + (V2-V3)sCc = 0');

eq3 = sym('gm3*V3 + (V3-V2)sCc = 0');

[V1,V2,V3] = solve(eq1, eq2, eq3,'V1','V2','V3');

%

[num, den] = numden(V2);

num = collect(num,Vin)

den = collect(den,Vin)

%%

Matlab计算结果如下：

num=gm1R1gm2 R2 (1+s*Cc/gm3)

den=as^3+bs^2+c*s+1

其中a=R1R2C1C2Cc/gm3

b=R1*C1*Cc/gm3 + R2*C2*Cc/gm3 + R1*R2*C1*(C2+Cc)

  c=Cc/gm3 + R1*C1 + R2*(C2+Cc) + gm2*R1*R2*Cc

进行简化，

den=as^3+bs^2+c*s+1

其中 a=R1R2C1C2Cc/gm3

b≈R1*R2*C1*(C2+Cc)

   c≈gm2*R1*R2*Cc

** 极点的推导：**

假设3个极点分别为p1、p2、p3，其中p1为主极点，p2为次极点，p3为次次极点，则

Den = (1-s/p1)(1-s/p2)(1-s/p3)= as^3 + bs^2 +c*s +1

a=-1/(p1p2p3)

b=1/(p1p2)+1/(p1p3)+1/(p2p3)≈1/(p1p2)

c=-(1/p1+1/p2+1/p3)≈-1/p1

联立上面几个式子，假设p1<

p1 = -1/(gm2R1R2*Cc)--------和常规miller补偿的结论一样

p2 = - gm2/C1*Cc/(C2+Cc)

p3 = -gm3/C2Cc*(C2+Cc)

验算：如果C1=0.5pF，C2=Cc=2pF，gm2=gm3=4mS，代入上面的结果，得到p3/p2=gm3/gm2=1。显然没满足p2<

如果不能做到gm3>>gm2，那p2<

** 零点的推导：**

LHP零点：-gm3/Cc

仿真验证：

1. gm3=gm2=4mS
   
   
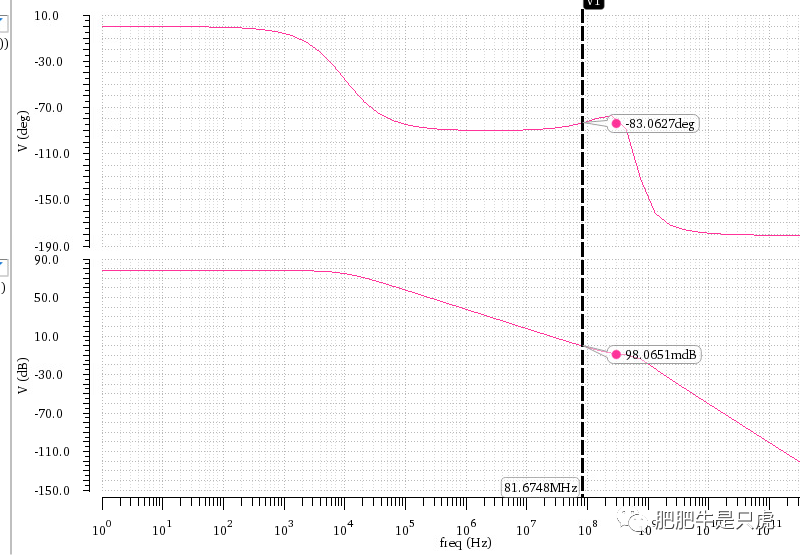
2. gm2=4mS，gm3=20mS

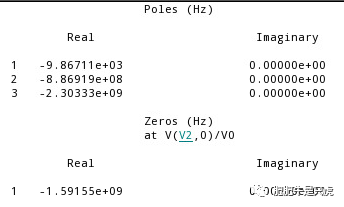
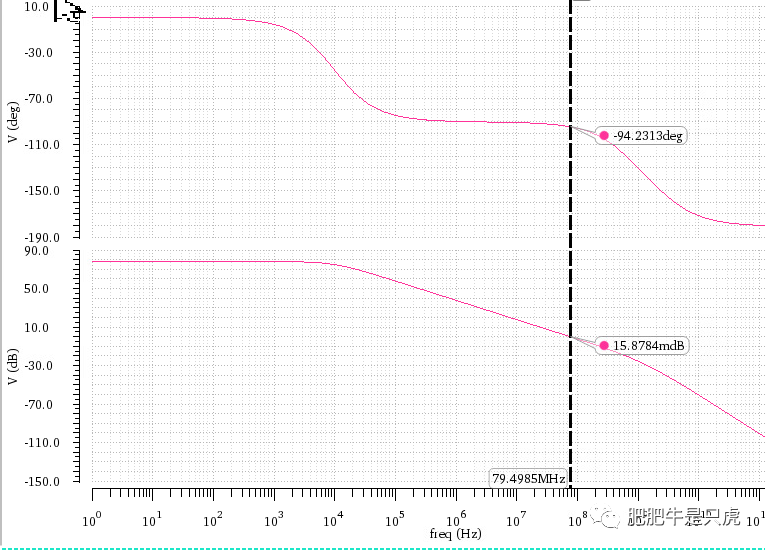
结论：

1. 采用电流跟随器结构消除前馈通道的Miller补偿方案，主极点和常规Miller补偿一样。除此以外，还存在2个极点一个零点，均为左半平面。
2. 吴金老师在他的“CMOS模拟IP线性集成电路”一书中给出了次极点的近似公式：gm2≈gm2/C2*Cc/C1，进而给了一个结论：“电流跟随器模式下的高频p2极点向外增加了Cc/C1倍，由于Cc>>C1，电流模式下的高频次极点频域更高，频率补偿的效果更明显。”根据上面的推导，这个结论需要附加一个前提条件：gm3>>gm2。对于更加一般的情况，这里的极点分布更加复杂。
3. 在实际电路设计中，如果不满足gm3>>gm2，则很容易引入一对共轭复极点。想要满足gm3>>gm2，常规结构的Source Follower需要较大的静态电流。或许可以考虑采用“Super Source Follower”，以较低的功耗实现gm的倍增（将gm倍增一个MOS的本征增益）。后面找时间验证下。
4. 总体上，感觉不管是“电压跟随”还是“电流跟随”，和常规的“Miller补偿+调零电阻”方案相比，没有明显优势。一顿操作猛如虎，效果原地杵。