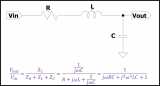
使用(s域)传递函数分析串联RLC电路系统。
线性非时变系统定义给我们带来了许多数学工具,也包含卷积积分,傅里叶变换和拉普拉斯变换。这些工具曾经是我学生时代的梦魇,以至于它们对我来说不是物理电路,也不是系统,更不是数学。现在鼓起勇气,再次入梦。
注,如无特殊声明,本文中提到系统均为线性非时变系统。
分析下图RLC电路。
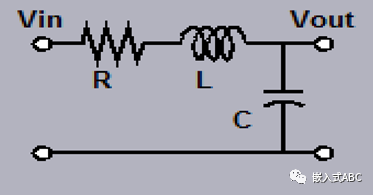
引入(运算)阻抗得到电路传递函数如下,这是一个二阶系统。
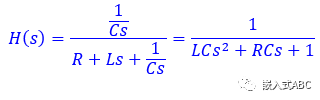
以后我们也会讨论到,即使不执行拉普拉斯反变换,不需要求得最后的时域解也能够分析RLC电路系统的某些特征。
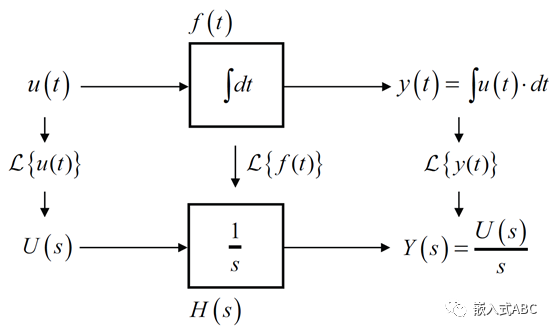
传递函数
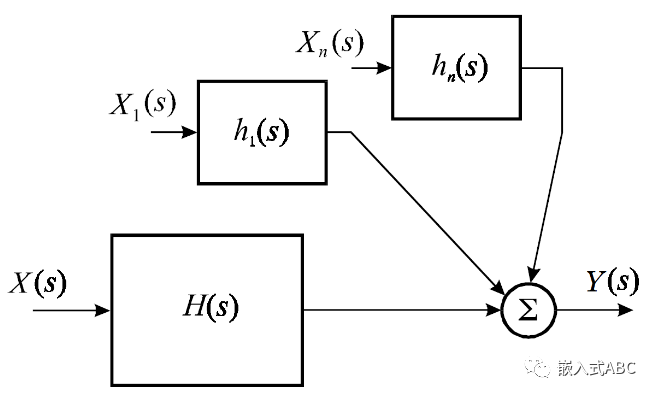
传递函数是一个数学模型,表示依照每个可能输入值输出的行为,即系统的传输增益。输入值定义为激励,在传递函数定义中激励必须为独立激励,而非受控激励。输出值定义为响应。
s域(复频域)系统传递函数为
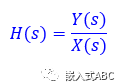
X(s)为激励拉普拉斯转换函数,Y(s)为响应拉普拉斯转换函数。
这里还有一个关键假设,即系统的所有初始条件均为零。或者按照电路课本中说法为零状态响应。当然若初始条件不为零时,拉普拉斯变换也会将初始条件适当地转换为激励函数以得到电路的全响应(当然包含零输入响应)。不过这些初始条件转换的激励对应响应的传输增益(或者说传递函数),不同于前面定义的传递函数。
定义初始条件拉普拉斯转换函数为X i (s),相应传递函数为H i (s)。当然也可以推广到为多输入系统。由叠加定理可得
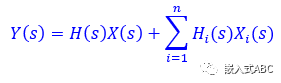
域
域是分析信号与系统的不同视角。简单说基于自变量t或函数f(t)的分析视角为时域,基于自变量jω或函数F(jω)的分析视角为频域,基于自变量s=σ+jω或函数F(s)的分析视角为复频域。
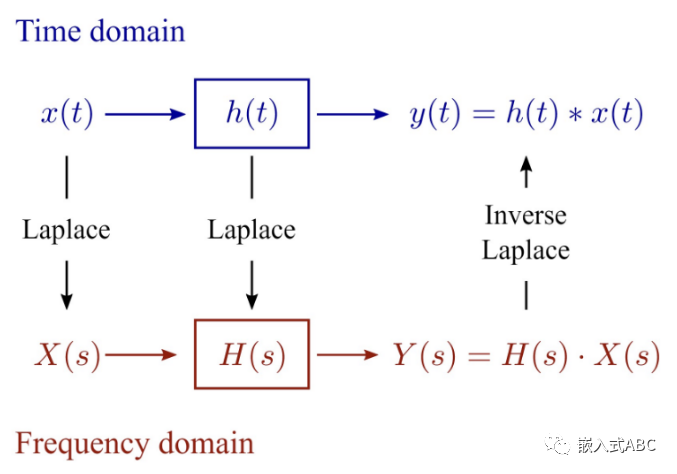
时域
时域对应于真实世界。我们已经习惯了时域,习惯了时间,时间并被定义为这个世界的一个维度。
麦克斯韦方程组也基于时域。于是(模拟)电路系统中,对于任意输入信号,时域分析法提供了一种分析电路系统特性(输入输出之间特定关系)的方法。微分方程提供了研究这一问题的方法,它利用导数概念来求解函数在某一点附近的变化率。这是一个用于表示函数在输入量变化了一定值时,输出量变化率的数学工具。于是上述RLC串联电路时域传递函数或响应的求解就是二阶齐次微分方程的求解。微分方程求解是另一个梦魇。
而且让我不解的是为什么频域或复频域比我们已经习惯了的时域在理解信号/电源完整性(阻抗概念)和电路系统稳定性等问题中更加具有洞悉力。
频域
傅里叶变换方程
接收某个时间函数并输出频率函数,告诉我们信号中含有那些频率或正弦曲线。
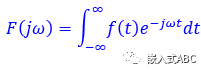
欧拉等式方程
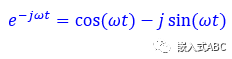
代入傅里叶变换方程得到
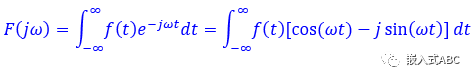
正弦波是频域中唯一存在的波形,正弦波是频域的语言。时域中任何波形都可由正弦波的组合完全且唯一地描述。
电路系统中傅里叶变换提供了非正弦周期电流电路的一种新的分析方法-谐波分析法,它是正弦电流电路分析方法(适用于正弦稳态分析的相量法)的推广。或者说它比正弦电流电路分析方法多了一个维度,在频谱概念中将会体会到这一点。傅里叶变换同样适用于非周期性电流电路(如瞬态响应中脉冲信号/冲击响应)的分析,只不过其频谱将由离散频谱变为连续频谱。
s****域(复频域)
拉普拉斯变换方程
拉普拉斯变换告诉我们函数中存在那些正弦曲线和指数曲线。
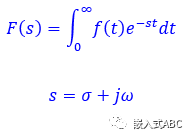
代入拉普拉斯变换方程得到
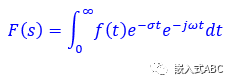
傅里叶变换是拉普拉斯变换的一种特例。一个函数的拉普拉斯变换就是该函数乘于一个指数项的傅里叶变换,对σ在实数域上的所有值,执行此操作,即可获得整个拉普拉斯变换。拉普拉斯变换比傅里叶变换又多了一个维度。
拉普拉斯变换常用于研究反馈系统的全响应,包括瞬态响应,如脉冲冲击或阶跃输入产生的响应。即系统对初始条件或突然施加信号的时间响应,而傅里叶变换主要关注系统的稳态响应。
拉普拉斯变换的性质
(时域)导数性质
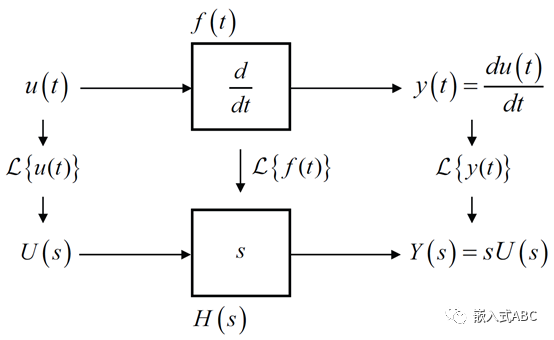
(时域)积分性质
拉普拉斯变换的另一重要特点,即拉普拉斯变换的性质可以让我们把微积分运算转化为代数运算。
总结
许多情况下傅里叶变换和拉普拉斯变换或者频域和复频域比时域更具有洞悉力,能更快的找到解决方法。
而且让我不解的是为什么频域或复频域比我们已经习惯了的时域在理解信号/电源完整性(阻抗概念)和电路系统稳定性等问题中更加具有洞悉力。
也许这来自于(正弦与指数等)几何函数的理解与空间维度的增加或降低,给我们带来直观的理解。
-
串联电路
+关注
关注
6文章
160浏览量
25781 -
傅里叶变换
+关注
关注
6文章
442浏览量
42732 -
拉普拉斯变换
+关注
关注
1文章
32浏览量
10199 -
RLC电路
+关注
关注
2文章
26浏览量
7216
发布评论请先 登录
相关推荐
放大器的传递函数-误差放大器、电压放大器、电流放大器的传递函数导出
线性电路传递函数的快速分析技术
基于Butterworth标准传递函数设计
传递函数极点和零点的影响是什么
传递函数是怎么定义的以及如何写出传递函数?
传递函数的频率特性




 使用(s域)传递函数分析串联RLC电路系统
使用(s域)传递函数分析串联RLC电路系统
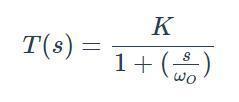










评论