直方图测试模数转换器(ADC)介绍

关键点:

直方图测试是确定模数转换器（ADC）静态参数的最流行方法之一。

直方图测试使用统计分析来确定ADC的过渡点，而不是直接测量过渡点。

线性斜坡直方图测试方法可以用于测量ADC的微分非线性度（DNL）误差。

摘要:

直方图测试是测试ADC静态参数的最受欢迎的方法之一。该方法通过分析ADC输出的统计数据来确定过渡点，能够在给定的测量时间内实现接近理论最优精度。与传统的伺服环测试方法相比，直方图测试方法对于高噪声水平下的ADC具有更好的效率。线性斜坡直方图测试是一种常用的直方图测试方法，可以用于测量ADC的微分非线性度（DNL）误差。该方法使用线性斜坡输入信号，并通过统计ADC输出来计算过渡点的宽度。除了DNL误差测量之外，直方图测试还可以用于测量ADC的整体非线性度（INL），但由于测量误差的累积和输入信号非线性度的限制，INL的测量更加困难。

直方图测试是确定模数转换器 (ADC) 静态参数的最流行的方法。在本文中，了解直方图测试的基础知识以及如何使用线性斜坡直方图测试的细节。

静态线性测试对于模数转换器 (ADC) 制造的经济性非常重要，这就是为什么学术界和工业界的研究人员投入大量工作来开发更高效的 ADC 测试方法。

本系列的上一篇文章介绍了用于测试 ADC 静态参数的伺服环路方法。在本期中，我们将总体讨论直方图方法，并特别探讨线性斜坡直方图测试的用途。

不过，首先让我们看一下伺服环方法的主要缺点，正是这些缺点使得开发这种替代测试方法成为必要。

伺服环路方法：ADC 噪声影响

虽然伺服环路方法是一种流行的工业测试技术，但它无法为具有较大输入参考噪声的 ADC 提供最佳效率。它在给定测量时间内的精度明显低于代表理论最佳精度的 Cramér-Rao 界限。图 1 比较了伺服环路测试的性能（表示为“传统”图）与 Cramér-Rao 界限预测的精度。

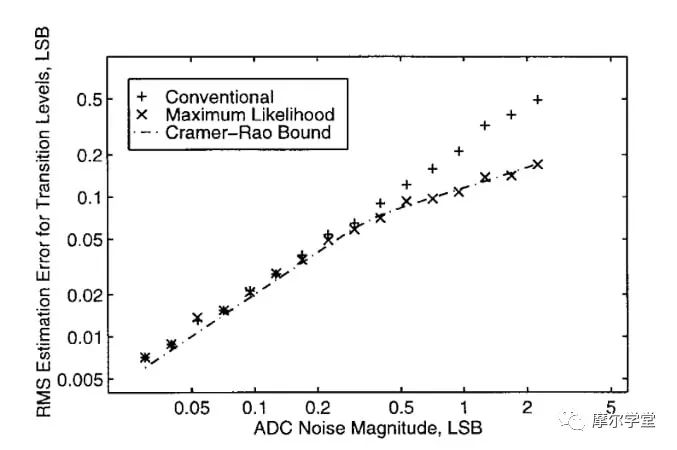
*图 1.*伺服环路测试性能精度与理论最佳值的比较。图片由P. Capofreddi提供

正如您所看到的，伺服环路方法无法在较高噪声水平下提供最佳效率。

对于输入参考噪声足够低的 14 位 ADC，伺服环路方法可能会令人满意地工作。然而，当今许多高分辨率 ADC 都具有高输入带宽，导致峰峰值、输入参考噪声超过 2 LSB（最低有效位）。这就是为什么我们需要能够导出 ADC 传输函数（无论其噪声水平如何）的测试方法。

ADC 的直方图测试

直方图测试也称为代码密度测试，是迄今为止测试 ADC 静态参数最流行的方法。通过该方法在给定测量时间内实现的精度非常接近 Cramér-Rao 界限指定的理论最佳值（图 2）。

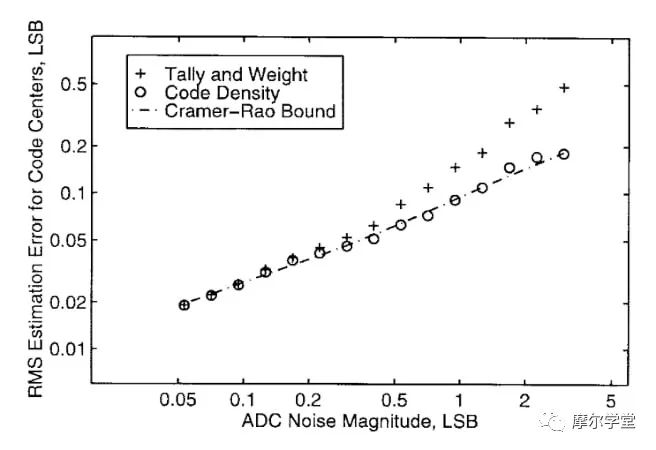
*图 2.*与理论最佳值相比的直方图测试性能精度。图片由P. Capofreddi提供

与直接测量 ADC 转变点的伺服环路方法不同，直方图方法使用转换器输出的统计分析来确定转变点。图 3 说明了直方图测试背后的基本思想。

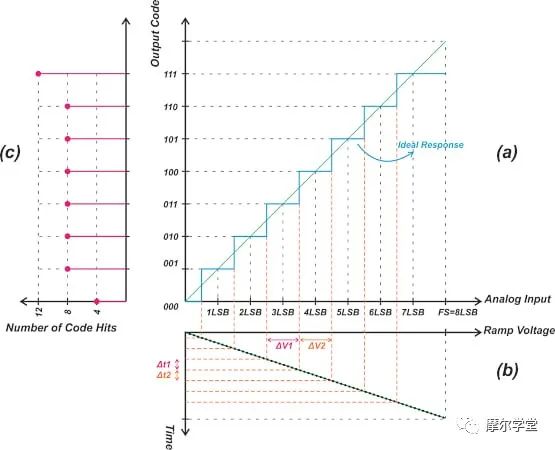
*图 3.*从右上角顺时针方向 — 理想 3 位 ADC 的传输特性、应用于 ADC 输入的满量程斜坡的旋转波形以及该波形的旋转直方图。图片由 Steve Arar 提供

图 3 可分为三个图，上面用字母表示。图 3(a) 显示了理想 3 位 ADC 的传输特性。图 3(b) 显示了应用于 ADC 输入的满量程斜坡的旋转波形。假设斜坡有固定的坡度；我们知道理想 ADC 的传递函数具有统一的步长。

例如，考虑对应于代码 011 和 100 的步骤。这两个步骤具有相同的宽度，因此斜坡信号应在步骤的转换点之间产生相同的电压变化（ΔV1 = ΔV2�2）。自从ΔV1V1= ΔV2，并且斜坡的斜率是恒定的，因此Δt1 = Δ�2t2这意味着斜坡输入在相同的时间内落入不同代码的输入范围内。换句话说，ADC 在每个输出代码上花费相同的时间。

基于此观察，我们可以收集大量输出样本并创建代码出现次数的直方图。直方图中的每个“bin”代表一个输出代码，每个bin的计数给出了该代码出现的次数。该计数与 ADC 传输函数中相应步长的宽度成正比。

图 3(c) 显示了此示例的旋转直方图 - 请注意，与代码 001 到 110 对应的 bin 都具有相同的计数（在本示例中为 8）。由于理想 ADC 中的第一步和最后一步通常定义为具有 0.5 LSB 和 1.5 LSB 的宽度，因此与代码 000 和 111 对应的 bin 的计数分别为 4 和 12。

有人可能会说第一个和最后一个代码实际上没有定义的宽度，因为第一个代码没有下限，而代码 111 没有上限。如果输入使 ADC 过载，这两个代码的出现频率可能会比预期更高。事实上，在实际直方图测试中，斜坡输入的幅度被选择为稍微超过 ADC 输入范围的两端。这样做是为了确保输入信号执行 ADC 的所有代码。因此，直方图方法中通常会忽略第一个和最后一个 bin。

直方图测试中常用的输入信号

图 3 所示的测试称为线性斜坡直方图测试。顾名思义，它使用斜坡输入。但是，直方图测试的输入不一定是斜坡 - 正弦输入是常见选择，并且可以使用具有已知概率分布函数 (PDF) 的任何输入。我们只需要计算理想 ADC 针对测试中使用的输入信号类型产生的输出 PDF。接下来，将测量的输出直方图与理论输出直方图进行比较，我们可以确定 ADC 的实际转变点。

使用线性斜坡直方图测试查找 DNL 误差

现在我们已经讨论了直方图测试背后的理论，接下来让我们使用直方图方法来查找示例 ADC 的微分非线性 (DNL) 误差。

首先，考虑图 4（红色曲线）中所示的非理想 3 位 ADC。

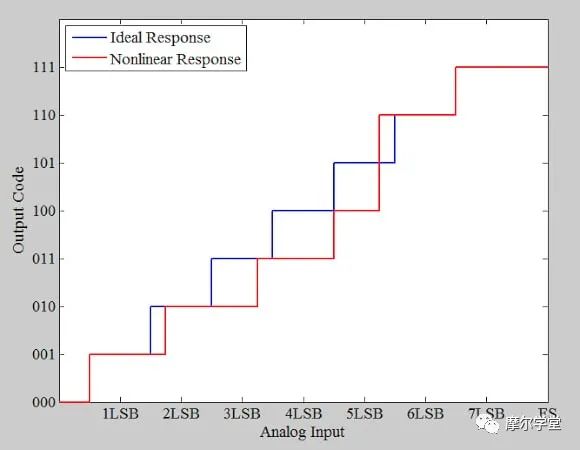
*图 4.*理想（蓝色）和非理想/非线性（红色）示例 ADC 响应。图片由 Steve Arar 提供

下面的图 5 中提供了该示例 ADC 的 DNL 图。请注意，缺少代码 5 (101) 。

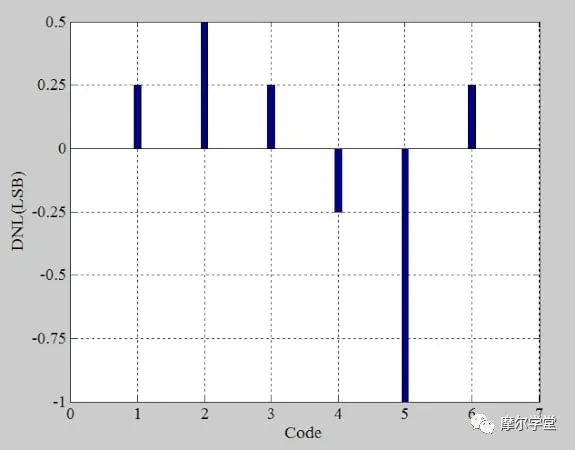
*图 5.*示例 ADC 的微分非线性。图片由 Steve Arar 提供

现在，使用上述满量程范围为 1 V 的传递函数，我们将以 40 kHz 的采样率对周期性斜坡进行数字化。图 6 显示了结果。

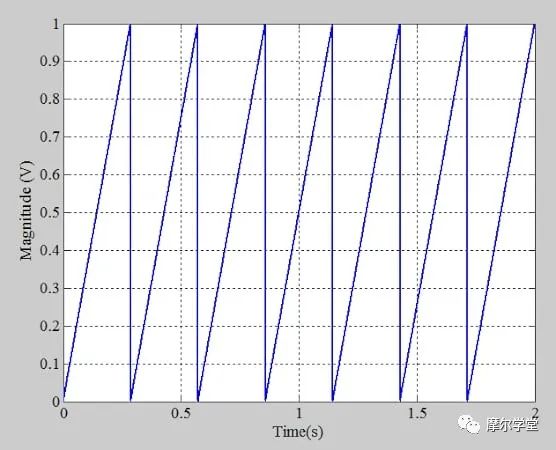
图 6.重复周期性线性斜坡输入，例如 ADC 直方图测试。图片由 Steve Arar 提供

斜坡周期（0.29 秒）远大于样本之间的时间，可以使用以下等式进行描述：

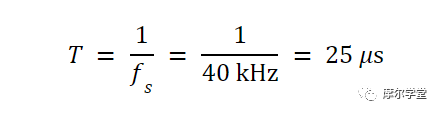
在哪里：

T是样本之间的时间（以秒为单位）

f s是采样频率（以 Hz 为单位）。

换句话说，斜坡输入相对于 ADC 采样率缓慢变化。这允许每个 ADC 代码被“命中”多次。

如果我们收集 80,000 个样本，我们会得到如图 7 所示的直方图。

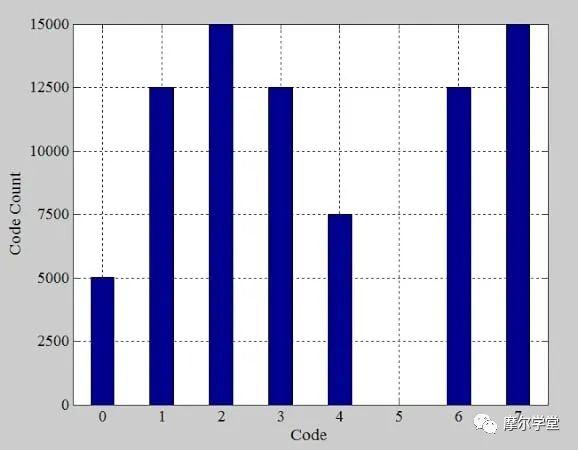
图 7.示例 ADC 的数字代码出现次数的直方图。图片由 Steve Arar 提供

Bin 5 的计数为零，表明代码 5 (101) 丢失。检查理想的 ADC 响应（图 4 中的红色曲线）表明，理想阶跃的宽度等于第一个和最后一个转换点之间的电压间隔除以之间的阶跃数：

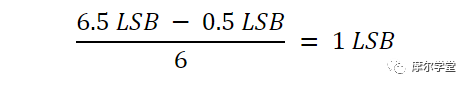
换句话说，理想台阶的宽度等于平均宽度。因此，具有理想宽度 (DNL = 0) 的代码出现的次数等于每个 bin 的平均代码计数。排除第一个和最后一个 bin，我们可以计算每个 bin 的平均命中数：

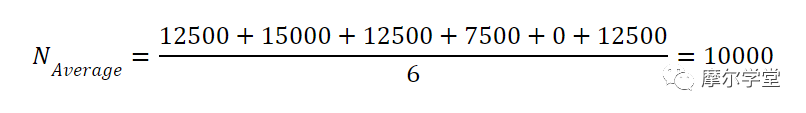
将 bin 高度除以平均代码计数即可得到图 8 中的归一化直方图。

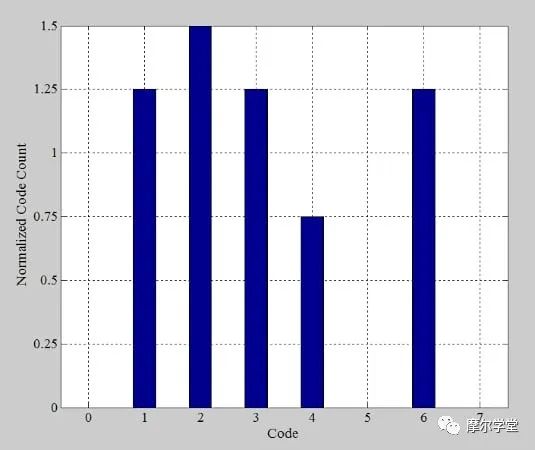
图 8. ADC 测试示例的正态直方图分布。图片由 Steve Arar 提供

归一化直方图以最低有效位指定代码宽度，我们之前确定理想步长的高度为 1 LSB。了解这一点后，我们可以通过从图 8 的归一化 bin 计数中减去 1 LSB 来生成 DNL 信息（图 9）。我们的结果与图 5 中的 DNL 图一致。

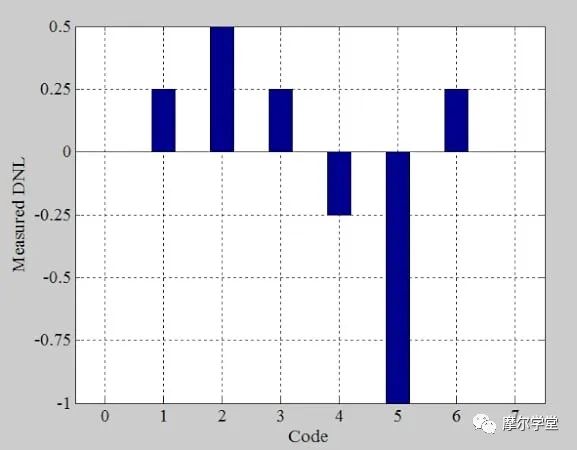
*图 9.*示例 ADC 的 DNL。图片由 Steve Arar 提供

如果采取适当的预防措施，线性斜坡直方图方法可用于测量 16 位或更高分辨率的 ADC 的微分非线性。准确测量积分非线性 (INL) 更具挑战性。

使用线性斜坡直方图测试来测量 INL

INL规范描述了实际传递函数的转变点与理想值的偏差。INL是DNL误差的累积效应，因此第m个代码的INL可以通过应用以下等式找到：

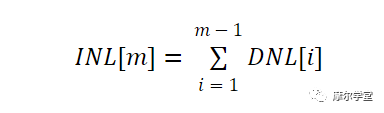
原则上，可以将DNL信息代入上述方程来确定INL误差。然而，在实践中，有几个误差源妨碍我们准确测量 INL。

测试电路参数和 ADC 特性的变化会导致 INL 测量误差。测试电路的变化可能来自电源、参考电压或输入信号发生器；可变的 ADC 特性包括偏移和增益。

上式中的求和本质上是在测量时间内累积所有这些误差，可能会导致10 位以上线性度的错误结果。

缓慢的测量系统会加剧漂移问题——如果它无法跟上 ADC 的高采样率，则收集所需数量的样本将需要更长的测量时间。如果漂移误差是限制因素，我们可以使用快速傅立叶变换 ( FFT ) 测试来测量 ADC 谐波失真，这是 INL 的主要影响。FFT 测试需要的样本数量要少得多，因此对漂移不太敏感。

此外，线性斜坡直方图测试假设输入斜坡是完全线性的。输入中的任何非线性都会直接转化为我们的 INL 测量中的误差。这限制了基于斜坡直方图的INL 测量对 12 位左右的 ADC的使用。为了解决这个问题，我们可以使用正弦输入进行直方图测试，因为可以轻松生成低噪声、纯正弦输入。






审核编辑：刘清