相噪是与哪种类型的抖动相对应？如何理解相位噪声与时间抖动的关系？

相噪是与哪种类型的抖动相对应？如何理解相位噪声与时间抖动的关系？

相位噪声与时间抖动是两个在信号处理领域中经常涉及的概念。在讨论相位噪声时，我们常常听到相位噪声和时间抖动的联系。因此，本文将探讨相位噪声和时间抖动的含义以及它们之间的关系。

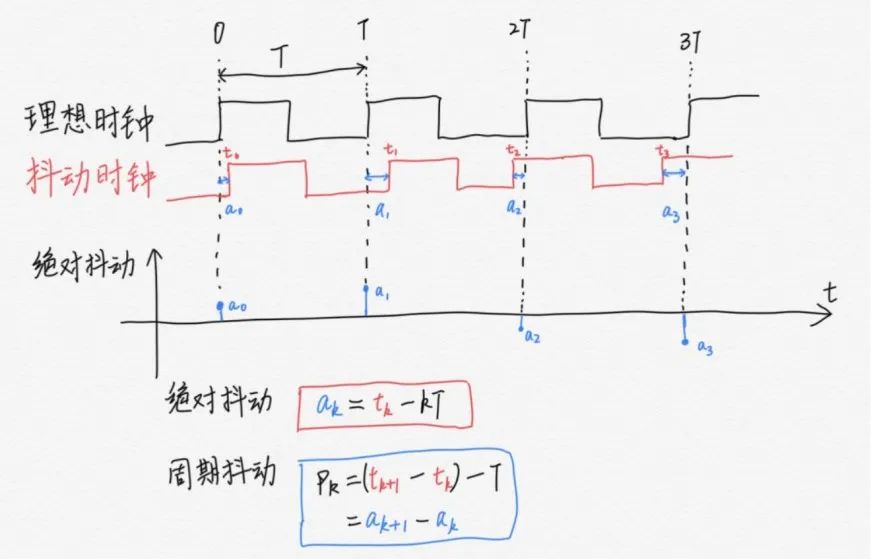
一、时间抖动

时间抖动是指信号的相位相对于一组参考信号的期望相位的偏差。它可以由以下数学公式表示：

$t_j = \frac{\phi_j}{2 \pi f_c}$

其中，$t_j$表示第$j$个采样点的时间偏移；$\phi_j$是该采样点的相位偏移；$f_c$是信号的中心频率。时间抖动的单位为秒。

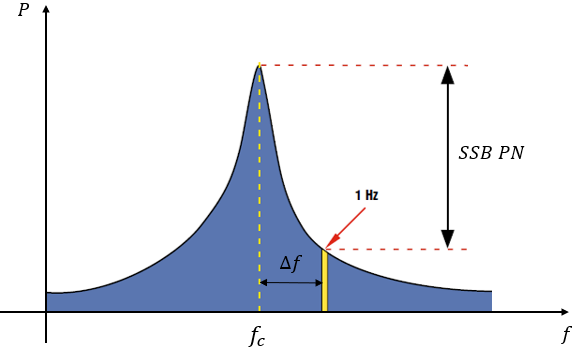
二、相位噪声

相位噪声是指信号的相位在频率上的偏移。它通常由相位噪声密度（PSD）来表示，即单位频率内相位噪声的平均功率。相位噪声的单位为弧度。

三、相噪

相噪是指在频率域内，信号的相位偏移噪声。相噪是相位噪声的一种体现。相噪和时间抖动之间有一个很重要的关系：在某些情况下，它们可以互相转换。

四、理解相位噪声和时间抖动的关系

相位噪声和时间抖动是两个不同的概念，但它们之间是有联系的。具体来说，相位噪声和时间抖动之间的关系可以通过以下公式表示：

$\Delta t_j = \frac{\Delta \phi_j}{2 \pi f_c \frac{\partial \phi}{\partial f}}$

其中，$\Delta t_j$是第$j$个采样点的时间偏移误差；$\Delta \phi_j$是该采样点的相位偏移误差；$\frac{\partial \phi}{\partial f}$是信号的相位斜率。

通过这个公式，我们可以看到，当信号的相位斜率越大时，时间抖动误差越小。相反，当相位斜率越小时，时间抖动误差越大。此外，如果相位噪声密度相同，但是信号的中心频率不同，那么时间抖动误差也会有所不同。

总之，相位噪声和时间抖动都是信号处理中非常重要的概念。相位噪声是指信号的相位在频率上的偏移，而时间抖动是指信号的相位相对于一组参考信号的期望相位的偏差。相噪是相位噪声在频率域内的体现，相位噪声和时间抖动之间有一个很重要的关系：在某些情况下，它们可以互相转换。通过深入理解这些概念之间的关系，我们可以更好地理解信号处理的内在机制，从而更好地应用它们来解决实际问题。