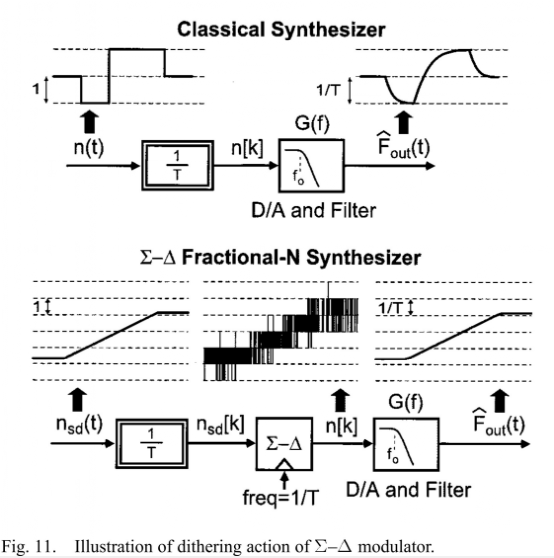
为了理解Σ-Δ调制器在频率综合器中究竟引起了啥影响,图11可以比较好的说明。需要指出的是,图11中把分频比的变化看作一个连续信号,这样的话能够比较好的在1/T的采样情况下,实现一个单位的输入变化(单位是分频比的code),反映到1/T的输出变化(范围是Hz)(1/T的缩放因子是采样导致的),以便使模型与真实情况一致。
在经典情况中,分频比是不变的,除非输出频率变化。而当分频比变化时,由于pll本征的低通特性,所以输出频率的变化相比于分频比变化的输入而言就好像经过了低通滤波器一样。
然而对于Σ-Δ小数N分频的频率综合器而言,分频比的变化频率非常高,而环路传输函数会提取出其中的低频成分,与Σ-Δ的输入信号nsd(t)一致(几乎可以达到任意高的精度)。
所以,频率调制精度与ref的频率无关,不过ref的频率越高,其达到指定频率精度的速度越快。
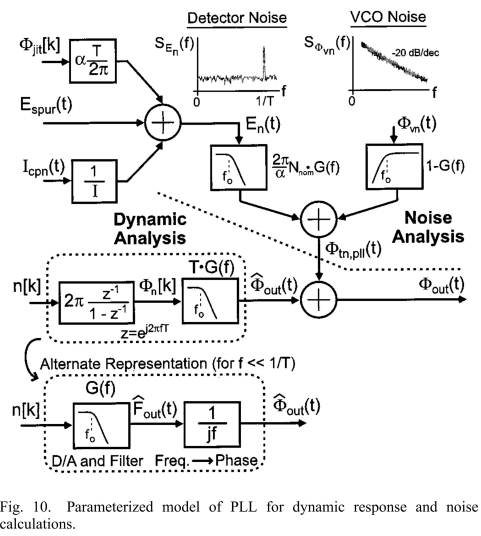
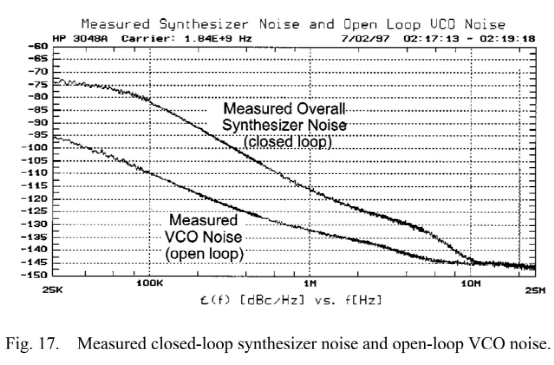
基于图10的频域模型(是根据前一篇推文中的时域模型转化而来:Z变换,S变换),我们添加上Σ-Δ的影响。量化噪声我们认为是白色的。
*Comments:图10中,G(f)T中的T从哪里来?这里fig表达的是分频比序列n[k]到输出的影响,所以从离散域进入连续域需要乘一个采样周期T,具体法则可以看下图:

首先,我们可以看到Σ-Δ的量化噪声逐次通过数字累加器、pll环路传递函数到pll的相位输出。数字累加器模型来源于分频器的积分效果,将Σ-Δ的噪声整形阶数降低了一阶(?可以认为Σ-Δ仅仅是提供了一个分频比上的一个抖动,分频比如果想要影响到相位,必然是要经过一个积分的)
Pll的传递函数的效果主要是作为一个低通滤波器,滤掉了高频的量化噪声。Σ-Δ的量化噪声在环路中提供了一个额外的噪声源。
不过他的出现并没有影响原有的各个噪声源到输出的影响并没有改变。(仅取决于环路传递函数和归一化分频数Nnorminal)
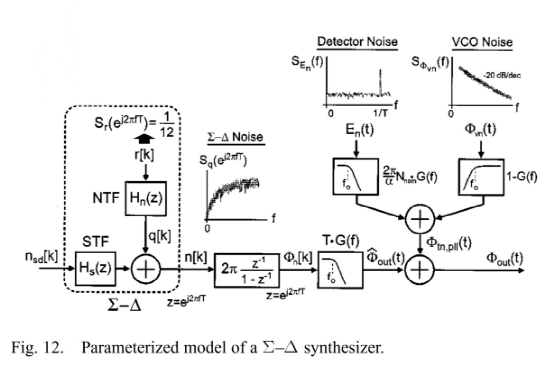
现在,pll输出的相位噪声贡献可以分为三部分:pfd+cp、VCO、Σ-Δ量化噪声(分频器对pn影响很小,假设不会引入噪声)根据图12,我们可以直接写出量化噪声与pll输出位置相位噪声的关系式:
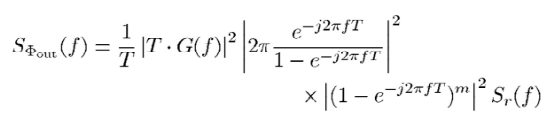
整理得到
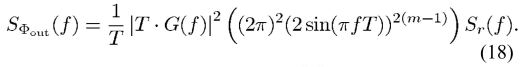
(事实上,对于一些输入而言,量化噪声并不是白色的,之后的深入理解Σ-Δ系列推送会有说明)如果量化噪声是白色的,那么其谱密度应当是1/12,这里量化台阶认为是1。(量化台阶为1在这里的意思就是实际控制分频器进行分频,分频比仅有两种选择)
事实上,18式已经可以观察到,Σ-Δ的NTF被削弱了一级,原因是分频器的积分效果。如果量化噪声真的可以被认为是白色的,那么量化噪声谱密度体现在pll的输出应当为(m-1)*20dB/dec的斜率上升。(当然前提是频率远小于采样频率)
所以这里就是为什么很多设计中使Σ-Δ的阶数与pll的阶数相同,因为pll的阶数事实上体现在g(f)的分母上,这样就可以抵消掉后面的Σ-Δ调制因式,还能多出来一个次数,换句话说,能够有效抑制高频的量化噪声。
具体在输出应当体现为-20dB/dec的滚降。这个滚降特性和VCO是一样的,能够不浪费,又够用,是比较恰当的设计考虑。
Comments:这里Σ-Δ的采样频率认为跟ref一样,如果不一样的,能否提高Σ-Δ的采样频率?收益如何?

-
低通滤波器
+关注
关注
14文章
485浏览量
47636 -
分频器
+关注
关注
43文章
448浏览量
50218 -
调制器
+关注
关注
3文章
875浏览量
45488 -
累加器
+关注
关注
0文章
50浏览量
9524 -
PLL电路
+关注
关注
0文章
92浏览量
6527
发布评论请先 登录
相关推荐
全数字锁相环的设计及分析
关于2.4 GHz的低噪声亚采样锁相环设计




 小数N分频锁相环频域模型与噪声分析
小数N分频锁相环频域模型与噪声分析











评论