示波器频域中的尼奎斯特频率和混叠现象

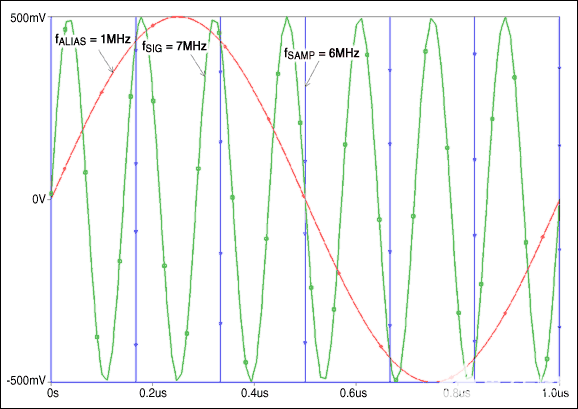
我们以示波器为例，看看频域中的尼奎斯特频率和混叠现象。

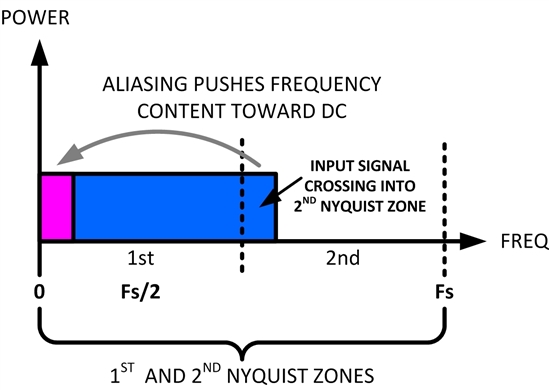
尼奎斯特频率是任何实时数字化示波器可进行采集而不会混叠的最高频率。此频率为采样率的一半。超过尼奎斯特频率的频率将会导致采样不足，从而出现混叠。尼奎斯特频率也称为折叠频率，因为在查看频域时，混叠的频率分量将从该频率向后折叠。

信号中的频率分量高于采样率的一半时发生混叠。因为 FFT 频谱受到该频率的限制，所以任何较高的分量都以较低（混叠）的频率显示。

下图对混叠做了说明。这是 990 Hz 方波的频谱，具有很多的谐波。方波的水平时间 /格设置可设置采样率，从而导致 FFT 分辨率为 1.91 Hz。从显示的 FFT频谱波形中可看到，高于尼奎斯特频率的输入信号分量要在显示中镜像（混叠），并反映在右边沿之外。

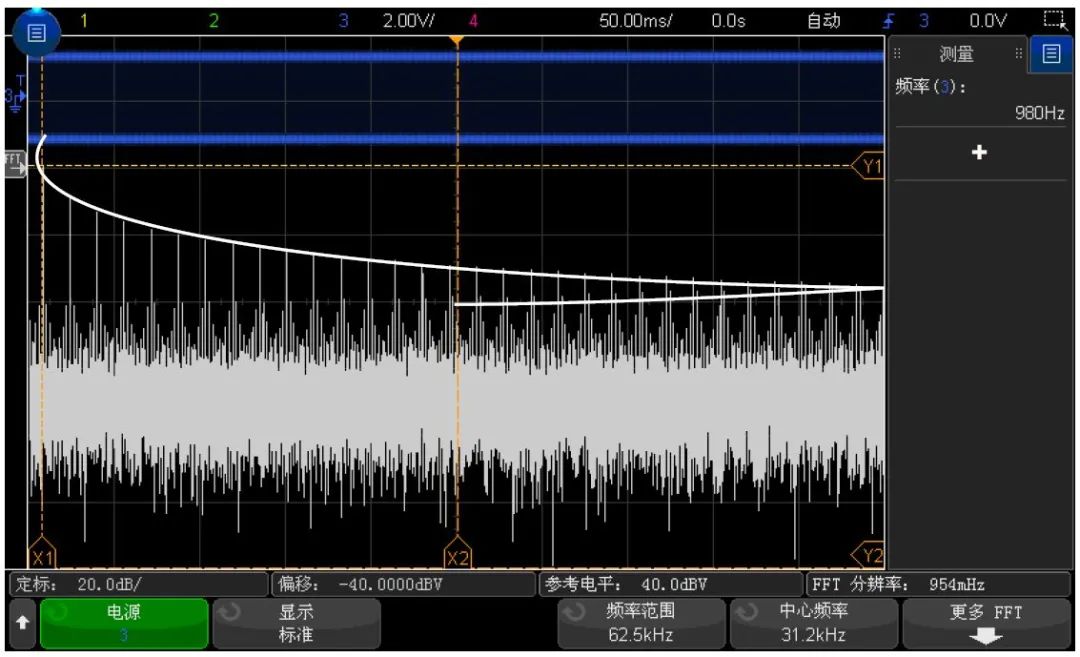
混叠

因为频率范围为从约等于 0 到尼奎斯特频率，所以防止混叠的最佳方式是确保频率范围大于输入信号中出现的高能量频率。

Nyquist 采样定理

数字测量应用所需的采用率为多少？一些工程师对于 Nyquist 理论深信不疑，并且认为只要采样率是示波器带宽的 2 倍便足矣。而其他工程师则不相信建立于 Nyquist 标准的数字滤波技术，更愿意使用采样率为带宽技术指标 10 至 20 倍的示波器。实际情况介于二者之间。

若要理解其中的原因，则必须了解 Nyquist 的理论及其与示波器频率响应之间的关系。Harry Nyquist 博士假设：Nyquist 采样定理对于具有最大频率 fMAX 的有限带宽信号，等间隔采样频率 fS 必须大于两倍的最大频率 fMAX，才能唯一地重建信号而不会有混叠现象。

Nyquist 采样定理可以归纳为两个简单规则，然而，对于 DSO 技术而言却不是那么简单。

1. 采集的最高频率分量必须小于采样率的一半。

2. 第二个规则是必须等间隔采样，而这一点经常会被遗忘。

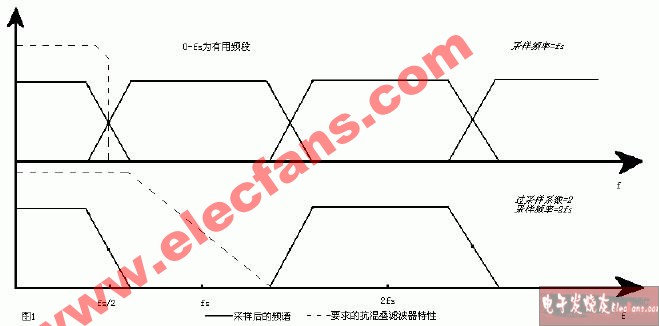
Nyquist 所称的 fMAX 就是我们通常所指的 Nyquist 频率（fN），它不同于示波器带宽（fBW）。如果示波器带宽恰好指定为 Nyquist（fN），则意味着示波器具有理想的砖墙式（brick-wall）响应，该响应在此相同频率下会完全衰减（如图 2 所示）。低于 Nyquist 频率的频率分量会完全通过（增益 =1），高于 Nyquist 频率的频率分量则会完全予以排除。然而，这种频率响应滤波器无法在硬件中实施。

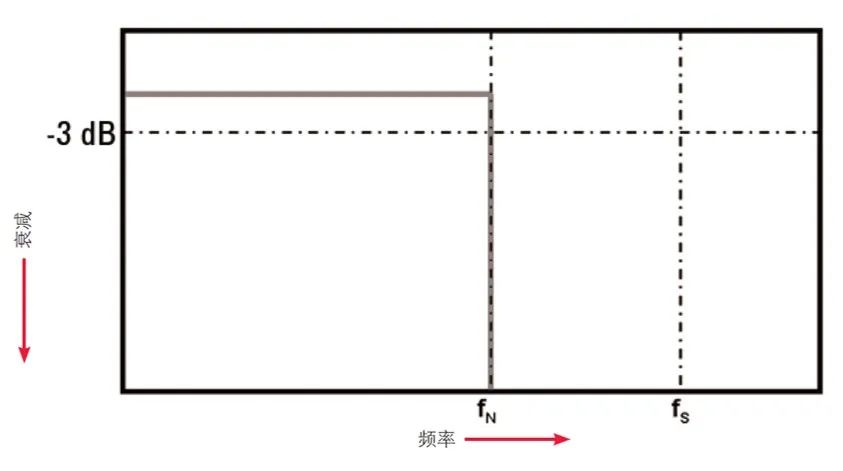
图 2：理想的砖墙式频率响应

带宽技术指标为 1 GHz 及以下的大部分示波器具有称为高斯频率响应的响应类型。当信号输入频率接近示波器的指定带宽时，测得的幅度会慢慢下降。信号在带宽频率下将会衰减 3 dB（~30%）。如果示波器的带宽正好指定为 Nyquist（fN）（如图 3 所示），输入信号超过这个频率的分量尽管衰减超过 3 dB，但也被采样（红色阴影部分），尤其当输入信号中包含快速边沿时，情况更是如此（测量数字信号时）。这种现象违背了 Nyquist 采样定理的第一条规则。

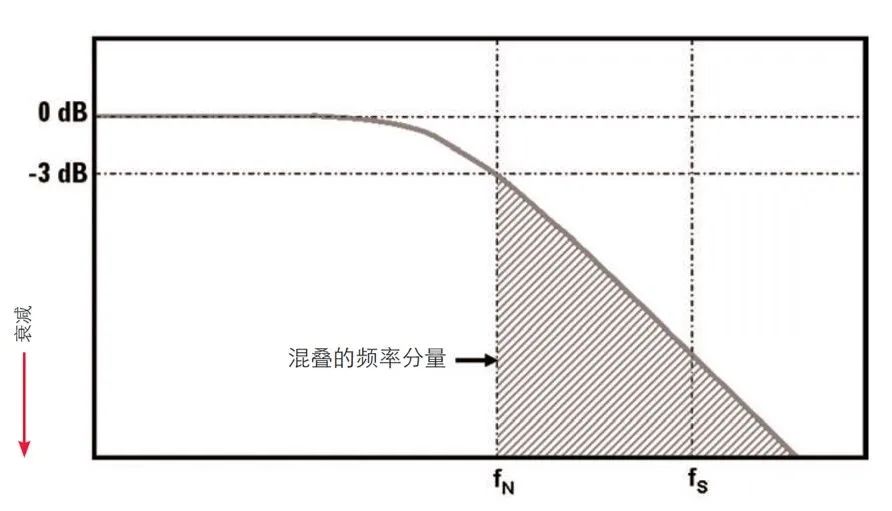
图 3：带宽（fBW）指定为 Nyquist 频率（fN）时，典型的示波器高斯频率响应

大多数示波器厂商不会将示波器的带宽指定在 Nyquist 频率（fN），不过也有部分厂商会这样做。但是，波形记录仪 / 数字转换器的厂商往往会将其仪器的带宽指定在 Nyquist 频率。现在我们看一下，如果示波器的带宽与 Nyquist 频率（fN）相同时会是什么状况。

图 4 显示：在三或四通道模式下工作时， 500-MHz 带宽的示波器正好以 1 GSa/s的速度进行采样。尽管输入信号的基本频率（时钟频率）处于 Nyquist 的范围内，但是信号边沿所包含的重要频率分量远落在 Nyquist 频率（fN）之外。仔细查看会发现，该信号的边沿具有不同程度的预冲、过冲和各种边沿速度，呈现出“不稳定” 的趋势。这就是混叠的迹象，它清晰地表明仅仅使用带宽为采样率 2 倍的示波器还不足以获得可靠的数字信号测量结果。

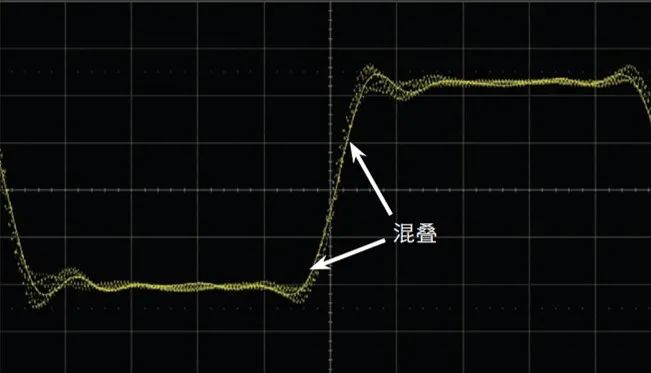
图 4：使用 1 GSa/s 采样率和 500-MHz 带宽的示波器进行采样所产生的混叠边沿

那么，示波器的带宽（fBW）的定义应该怎么关联到波器的采样率（fS）和 Nyquist 频率（fN）呢？为了尽量避免对超出 Nyquist 频率（fN）的频率分量进行采集，大多数示波器厂商将其具有典型高斯频率响应的示波器带宽指定为实时采样率的 1/4 至 1/5 或更低（如图 5 所示）。尽管以比示波器带宽大更多倍的速率采样可以进一步降低采集 Nyquist 频率（fN）之外频率分量的可能性，但是 4:1 的采样率与带宽比足以获得可靠的数字测量结果。

带宽技术指标在 2-GHz 和更高范围的示波器通常具有更陡峭的频率衰减响应 / 特征。我们将这种类型的频率响应称为“最大平坦度”响应。由于具有最大平坦度响应的示波器接近于砖墙式滤波器的理想特征，在这种情况下，超出 Nyquist 的频率分量衰减程度更高，因此无需进行多次采样即可很好地显示使用数字滤波的输入信号。理论上厂商可以将具有此类响应的示波器带宽（假设前端模拟硬件具备相应能力）指定为 fS/2.5。

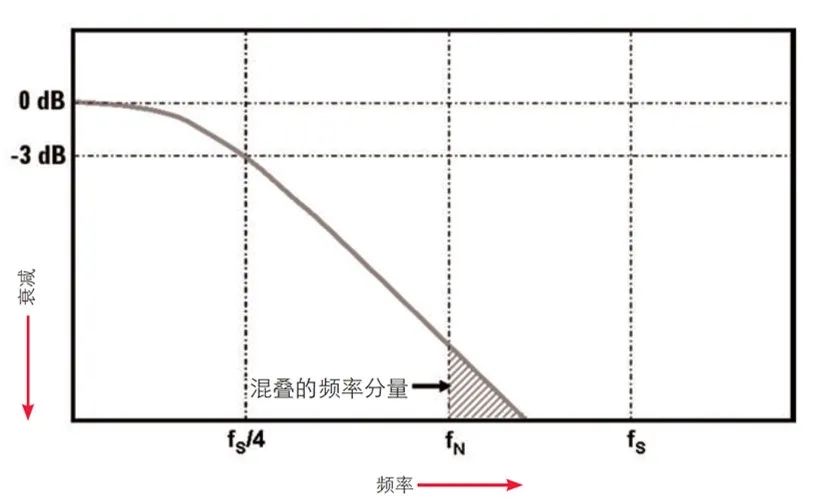
图 5：将示波器带宽（fBW）限制为采样率的 1/4（fS/4），可以降低 Nyquist 频率（fN）之上的频率分量

图 6 显示了 500-MHz 带宽的示波器捕获边沿速度在 1 ns（10% - 90%）范围的 100-MHz 的时钟信号。500 MHz 的带宽技术指标是精确捕获此数字信号的最小推荐带宽。这一特定的示波器能够在双通道工作模式下以 4 GSa/s 进行采样，或者在三或四通道工作模式下以 2 GSa/s 进行采样。图 6 显示的是 2 GSa/s 采样的示波器，其采样频率是 Nyquist 频率（fN）的两倍，带宽频率（fBW）的四倍。该图表明，采样率与带宽之比为 4:1 的示波器可以非常稳定而准确地表示输入信号。并且，借助 Sin(x)/x 波形重建 / 插值数字滤波技术，此示波器的波形和测量分辨率可达几十皮秒的量级。与我们之前图 4 所显示的例子（采用相同带宽的示波器，但仅为带宽（fN）两倍的速度进行采样）相比，波形稳定性和精确度的差别显而易见。

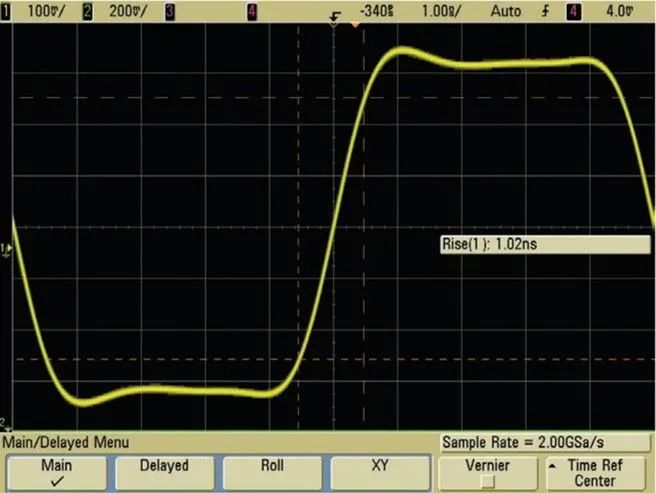
图 6：采用是德科技 500-MHz 带宽示波器以 2 GSa/s 的速率进行采样，可以精确测量这个边沿速度为 1 ns 的 100-MHz 时钟信号

那么，如果我们将采样率增大一倍，使其达到 4 GSa/s，再以相同的 500-MHz 带宽示波器（fBW x 8）采样，结果又会怎样呢？您可能会直观地认为该示波器将会获得更佳的波形和测量结果。但正如图 7 所示，您只能取得很小的改进。如果仔细观察这两个波形图（图 6 和图 7），您将会发现，以 4 GSa/s（fBW x 8）采样时，显示的波形中仅有轻微的预冲和过冲。但是，上升时间测量显示相同的结果（1.02 ns）。波形保真度略有提高的关键在于：当此示波器的采样率与带宽之比由 4:1（2 GSa/s）升至 8:1（4 GSa/s）时，没有引入其他的误差源。这就引出了我们的一个主题：如果违背 Nyquist 规则二会怎么样呢？Nyquist 强调必须等间隔进行采样。用户在评测数字存储示波器时，往往会忽视这一重要规则。

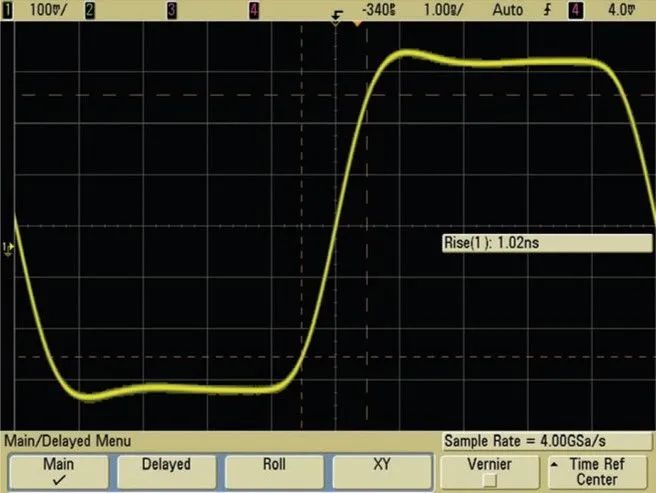
图 7：采用是德科技 500-MHz 带宽示波器以 4 GSa/s 采样，与 2 GSa/s 采样相比，对测量效果的提高微乎其微。

审核编辑：汤梓红