为什么要给雷达信号加窗？怎么加？

现代雷达对接收信号都进行了一些形式的采样，而对信号序列x(n)的截短也是不可避免，通常使用乘积来实现。为了减少频谱能量泄漏，可采用不同的截取函数w(n)对信号进行截断，通常称为加窗序列，简称为窗。

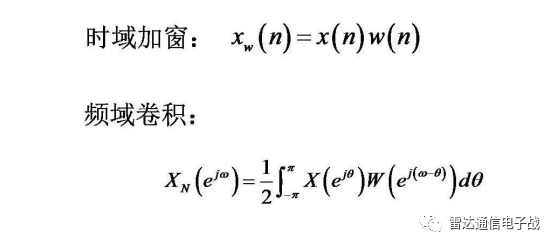
不同的窗函数对信号频谱的影响是不一样的，这主要是因为不同的窗函数产生泄漏的大小不一样，频率分辨能力也不一样。为了不影响截短序列的相位响应，通常需要窗函数保持线性相位。

典型窗函数

常用的窗有：矩形窗、汉明窗(Hamming)、汉宁窗(Hanning)、布莱克曼(Blackman)等。我们可以通过Matlab很容易的对序列进行加窗，也可以简单的看到窗函数的频率响应。

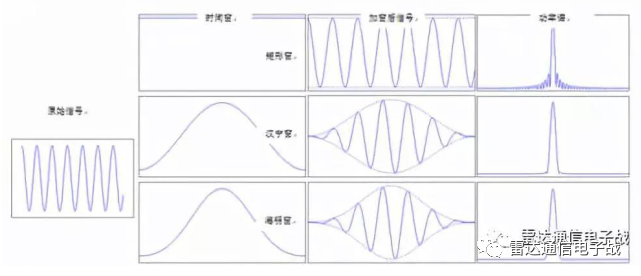
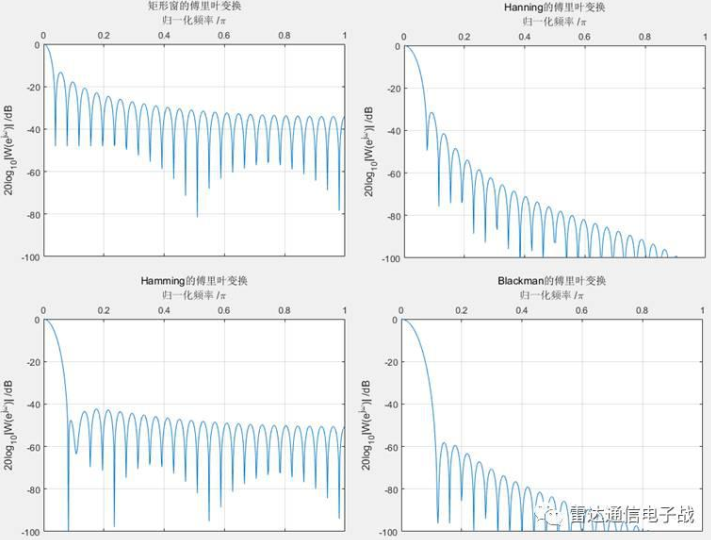
矩形窗的优点是主瓣比较集中，缺点是旁瓣较高，并有负旁瓣，导致加窗过程中带进了高频干扰和频谱泄漏。

汉宁窗又称升余弦窗，汉宁窗使主瓣加宽并降低，旁瓣则显著减小，从减小泄漏观点出发，汉宁窗优于矩形窗。但汉宁窗使主瓣加宽，相当于分析带宽加宽，频率分辨力下降。汉宁窗函数的最大旁瓣值衰减-31dB，但是主瓣宽度比矩形窗函数的主瓣宽度增加了1倍。

汉明窗也是余弦窗的一种，又称改进的升余弦窗，与汉宁窗的加权系数不同。汉明窗加权的系数能使旁瓣达到更小。汉明窗的第一旁瓣衰减为-42dB，其旁瓣衰减速度比汉宁窗衰减速度慢。汉明窗与汉宁窗都是很有用的窗函数。

为啥要加窗？

在时域上看，加窗其实就是将窗函数作为调制波，输入信号作为载波进行振幅调制。矩形窗对截取的时间窗内的波形未做任何改变，即只是截断信号原样输出。

更普遍地，绝大部分窗函数形状都具有类似从中间到两边逐渐下降的形状，只是下降的速度等细节上有所区别。降低截断引起的泄漏，所有窗函数都是通过降低起始和结束处的信号幅度，来减小截断边沿处信号突变产生的额外频谱。

不同的窗函数，产生泄漏的大小不一样，频率分辨能力也不一样。信号的截断产生了能量泄漏，而用FFT算法计算频谱又产生了栅栏效应，从原理上讲这两种误差都是不能消除的，但是我们可以通过选择不同的窗函数对它们的影响进行抑制。

时域加窗

通常时域上加窗更为普遍，时域截断效应带来了频谱的泄漏，窗函数是为了减小这个截断效应，被设计成一组加权系数w(n)。

域加窗在时域上表现的是点乘，因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程，相当于一组具有特定函数形状的滤波器，因此，原始信号中在某一频率点上的能量会结合滤波器的形状表现出来，从而减小泄漏。

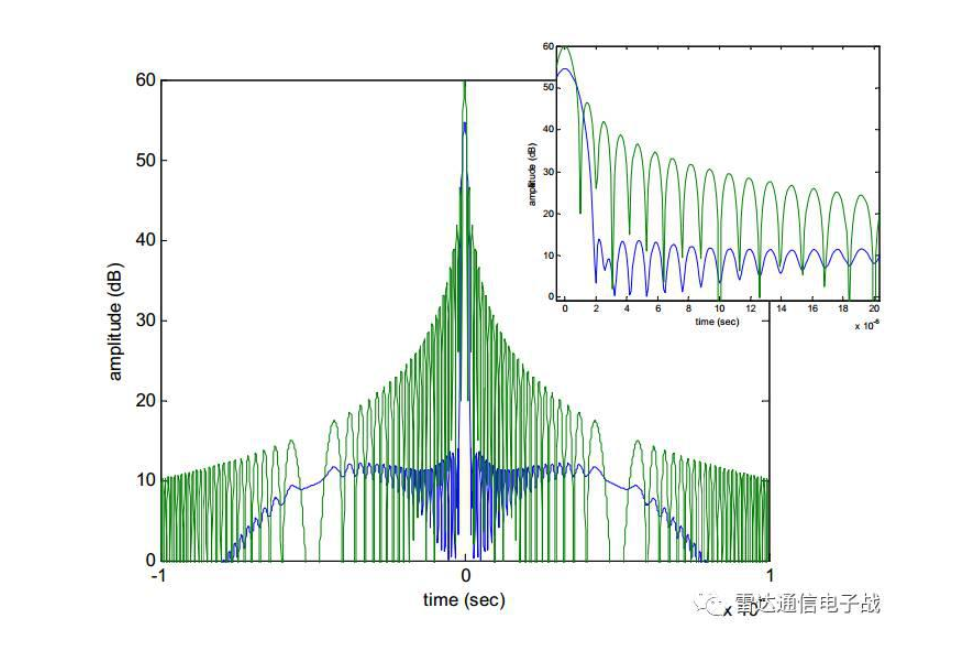
从上图可以看出对线性调频信号(LFM)的时域加窗会导致主瓣变宽而旁瓣得到明显降低，并且最大幅值也有所降低。

频域加窗

频域加窗在频域上表现为点乘，这是为了减小脉冲压缩后时域的距离向旁瓣，而对匹配滤波器的频率响应加窗。我们知道线性调频脉冲的频率响应近似为矩形，对其乘以窗函数可得到修正后的频率响应。

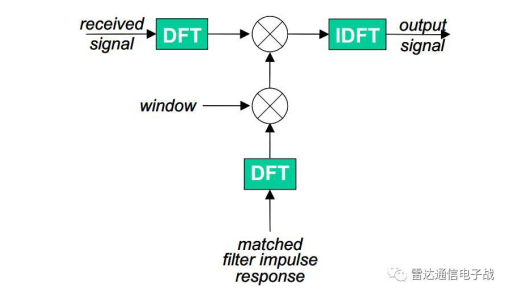
修正后的频率响应不再与发射的LFM信号匹配，因此输出峰值和信噪比都会有一定减小。从下图可以看出频域加窗对脉冲压缩结果的影响，导致主瓣变宽而旁瓣得到明显降低，并且最大幅值也有所降低。

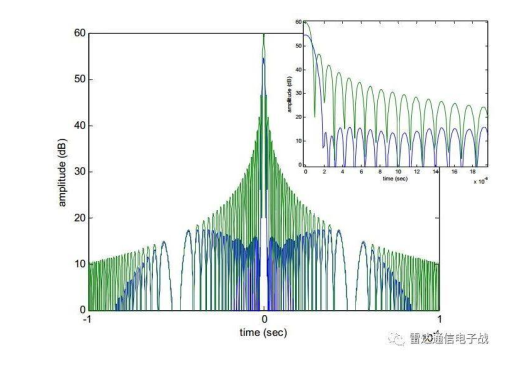
从下图可以对比发现时域加窗和频域加窗有一些共同的效果，也有一些不同的区别，例如旁瓣大小不同，旁瓣结构也有所不同等。其中蓝色是频域加窗后脉冲压缩后的结果，绿色是时域加窗后的结果。

加窗对频率和幅值的影响

傅里叶变换后主要的特征有频率、幅值和相位，而加窗对相位的影响是线性的，所以一般不用考虑，下面主要讨论加窗对频率和幅值的影响。

加窗对频率和幅值的影响是关联的，对于时域的单个频率信号，加窗之后的频谱就是将窗谱的谱峰位置平移到信号的频率处，然后进行垂直缩放。说明加窗的影响取决于窗的功率谱，也就容易理解为什么总常看到对窗特征主瓣、旁瓣等的描述。

主瓣变宽就可能与附近的频率的谱相叠加，意味着更难找到叠加后功率谱中最大的频率点，即降低了频率分辨率，较难定位中心频率。旁瓣多意味着信号功率泄露多，主瓣被削弱了，即幅值精度降低了。由于加窗计算中衰减了原始信号的部分能量，因此对于最后的结果还需要加上修正系数。

如何选择“窗函数”？

对于一次过程时间小于窗口的暂态信号或冲击波形，信号开始和结束处本身就是零，不存在截断引起的泄露，不需要加窗抑制，因此只需要用矩形窗即可。

在需要频率分辨率高时，使用旁瓣少的窗口，如汉宁窗，而矩形窗旁瓣太高，泄漏太大；在需要幅值准确时，还可以使用平顶窗。对于连续的周期性波形，可以结合不同的窗口获得所关注的结果。

审核编辑：汤梓红