量子材料中的自旋—动量锁定新效应简析

01 引 言

人工智能、计算机、芯片、集成电路、半导体产业等一系列耳熟能详的概念标志着信息化文明的繁荣昌盛。然而，随着信息处理器集成度的不断提高，器件进入了介观尺寸，摩尔定律正逐渐失效，现代信息化的硬件基础随之进入了发展瓶颈期。在介观领域，材料的量子效应显著，通常需要被妥善规避处理；而对一类新型材料的量子效应加以利用则有望实现新的器件原理。这样一类新材料被称为量子材料，包括电子关联相互作用显著或存在某种类型电子序(如超导、磁有序)的材料体系，或由于波函数的几何相位而呈现出奇特电子特性的体系。不同于主要依赖于单一电荷自由度的传统微电子学器件，量子材料的核心在于包含了晶格、电荷、自旋、轨道等多自由度耦合特征，因此可以表现出多种多样的新奇量子行为。其中，电子的另一内秉自由度——自旋，及其与电荷、轨道等多自由度的耦合效应，已显现出可用于突破瓶颈的巨大开发潜力。电子自旋的最大特点是二值性，即电子在稳态下可被区分为自旋向上(↑)和自旋向下(↓)两类，是一个天然的理想二进制信息载体。近几十年来，科学家研究自旋的产生、存储、输运、调控等信息处理过程，并逐渐发展形成了自旋电子学。而基于自旋的新一代器件，包括与半导体微电子工艺兼容的超高密度、大容量、非易失磁存储和逻辑存算一体化器件，成为后摩尔时代信息产业发展的主要方向之一[1]。

自旋电子学的材料基础是自旋极化材料。在一般的非磁性材料中，如果不考虑自旋轨道耦合，自旋向上(↑)和自旋向下(↓)的量子态在动量空间是处处简并的，即在能带上有ϵ↑n(k)=ϵ↓n(k)。自旋极化材料的典型特征是自旋上下的电子需要在能带上劈裂，即ϵ↑n(k)≠ϵ↓n(k)，也就是所谓的自旋劈裂。此时，在外电场作用下费米能级上的态密度通常有N↑≠N↓，这使得在输运中某一类自旋将占据主导，产生携带自旋信息的自旋极化电流。最传统的自旋极化材料为铁磁体，其能带由于磁交换相互作用发生Zeeman型自旋劈裂，如图1(a)所示，这使得携带自旋向上与自旋向下的电子占据数不一样，从而存在净自旋极化，即ρ=(N↑-N↓)/(N↑+N↓)。若通过外磁场翻转铁磁体的局域磁矩方向，自旋极化的方向也随之翻转。1988年，Grünberg和Fert分别独立构造了铁磁金属/非磁金属/铁磁金属的三明治结构器件，当两个铁磁体磁矩平行时，自旋极化方向相同，输运电子受到的散射小，电阻低；而当磁矩反平行时，自旋极化方向相反，散射大，电阻高，这就是著名的自旋电子学开山之作——巨磁阻效应[2，3]。该效应可用于制备磁读头器件，由于其微型化优势，大大提高了信息存储密度进而促进信息化发展，并于2007年被授予诺贝尔物理学奖。后来，基于铁磁材料的自旋极化，隧穿磁电阻、自旋转移力矩、自旋高频振荡等一系列自旋电子学效应被发现和研究，构成了传统自旋电子学的基础。

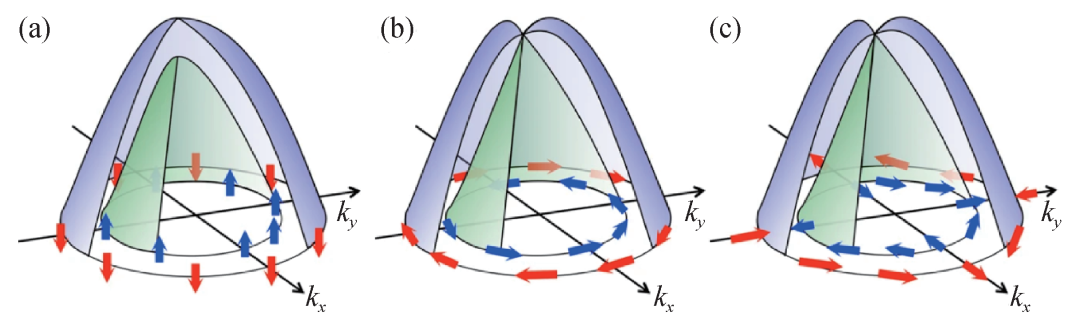
图1 三种典型的能带自旋劈裂示意图，包括(a)Zeeman型、(b)Rashba型和(c)Dresselhaus型(箭头表示自旋极化方向)

从对称性角度考虑，铁磁体是通过破坏时间反演对称性产生自旋劈裂，而在具有时间反演对称的非磁材料中，亦可通过破坏空间反演对称(包括表、界面)，并在自旋轨道耦合的协助下，在动量空间产生自旋劈裂的能带。与传统铁磁体不同，非磁体系在费米面处并无净自旋极化，而是由于自旋轨道耦合效应在特定动量上携带特定自旋信息，即自旋—动量锁定效应，从而在费米面处有形式各异的自旋织构(spin texture)，并可以通过电输运手段直接产生和探测自旋极化电流。因此，这类自旋极化材料在新兴的自旋电子学效应，如自旋轨道力矩中，扮演着重要的角色。最近几年，基于对称性研究，自旋—动量锁定效应又进一步扩展到具有空间反演对称的材料以及无自旋轨道耦合的反铁磁体中。本文将首先介绍自旋—动量锁定的概念及应用，然后介绍通过引入实空间原子层与反铁磁局域磁矩这两种自由度产生的自旋—动量锁定新效应：“隐藏自旋极化”和“反铁磁自旋极化”，最后概述由此发展起来的新型自旋电子学效应。

02 自旋—动量锁定效应

从自旋的起源来说，自旋极化现象是一种相对论的量子效应。从相对论量子力学的基本原理出发，当外磁场B引起Zeeman劈裂时，能级劈裂大小可描述为∆ϵ=B∙σ>，其中g为朗德因子，μB为玻尔磁子，σ为自旋泡利矩阵。对于自旋极化材料来说，其自旋劈裂效应也可由哈密顿量H(k)=Beff(k)∙σ简单描述，其中等效磁场Beff的可能来源有两类，即磁交换作用与自旋轨道耦合作用。前者源于泡利不相容原理，是自旋与自旋之间的相互作用，而后者是电子自旋与自身轨道的相互作用。自旋轨道耦合作用可描述为Hsoc=eℏ(∇V×p)∙σ/(4m2c2)，其中∇V为电势梯度，p为动量算符，其产生的等效磁场Beff(k)是动量依赖的，在时间反演对称性下有Beff(k)=-Beff(-k)，而在空间反演对称性下则有Beff(k)=Beff(-k)。因此，在非磁材料(具有时间反演对称)中，仅当空间反演破缺时，才有Beff(k)≠0，从而引起能带自旋劈裂。并且，不同于Zeeman型劈裂，这种自旋劈裂也是动量依赖的，即自旋—动量锁定效应。最经典的自旋—动量锁定效应是Rashba型和Dresselhaus型自旋劈裂[4，5]，分别对应于螺旋的(helical)和非螺旋的自旋织构，如图1(b)，(c)所示。为了理解这两种效应，人们通常将体相空间反演对称破缺与Dresselhaus效应联系在一起，而将Rashba效应归结于结构空间反演对称破缺，一般存在于表界面等二维结构中。然而在2011年，显著的Rashba自旋劈裂在极性半导体BiTeI的体态中被发现[6]，之后的许多研究亦表明上述的唯象描述远不足以理解自旋—动量锁定效应，其微观机理仍有待进一步澄清。

Rashba与Dresselhaus效应早在上世纪五六十年代就被发现，随着材料器件制备工艺和实验探测手段的不断发展，直到大约15年前才开始在自旋电子学领域大放异彩。21世纪初，自旋场效应晶体管的概念被提出，即利用外加门电压调控自旋轨道耦合作用的强度，从而实现对输运电子自旋信息的调控。但该效应由于对电子自旋的相干性要求比较高，目前未能实现高效稳定的实用器件。2009年前后，自旋轨道力矩效应被发现，在重金属/铁磁金属界面通过由自旋轨道耦合作用引起的自旋极化电流，进一步产生自旋力矩用以实现对铁磁金属磁矩方向的调控。自旋轨道力矩相比于自旋转移力矩，在器件结构上更简单并且功耗更低，因此引发了研究热潮并持续至今。另一个引人关注的自旋轨道耦合相关效应是自旋霍尔效应，即对材料施加纵向电流时，在横向会产生自旋流，其逆效应在电探测自旋流方面发挥着重要作用。近年来，随着这些基于自旋轨道耦合的自旋电子学效应被发现和深入研究，以及相应自旋极化被拓展至拓扑材料和反铁磁材料等，形成了富有应用潜力的“自旋轨道电子学”新兴领域[7，8]。

如上所述，空间反演破缺和自旋轨道耦合似乎是实现自旋—动量锁定效应的两个必不可少的前提条件，果真如此吗？随着进一步研究自旋、轨道、晶格等多自由度耦合与对称性之间的关联，人们发现并非如此，并先后发展出了两个新领域，包括隐藏自旋极化和反铁磁自旋极化。我们在下文中逐一介绍。

03 自旋—动量—层锁定效应：隐藏自旋极化

让我们重新审视自旋轨道耦合作用，尽管其中的晶体电势梯度要求空间反演破缺，但该作用仅属于电子的自旋与其自身原子轨道之间，是一种局域效应，即只要局部原子的空间反演对称性破缺，自旋轨道耦合作用便可发挥影响。据此，笔者与合作者于2014年提出了“隐藏自旋极化”的概念[9，10]，即在空间反演的非磁性材料中，若有原子或原子组成的层(记为α)的局部环境是空间反演破缺的，便可存在由自旋轨道耦合引起的“局部”自旋极化Pα(k)，即Pα(k)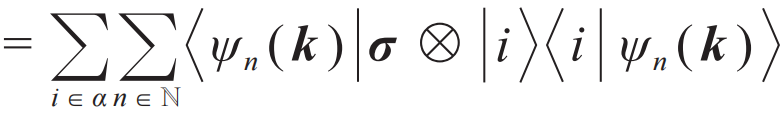



，其中i为局域原子轨道，ℕ表示简并能带求和。互为空间反演的两个原子或原子层(α和β)，其局部自旋极化方向相反，即Pα(k)=-Pβ(k)，使得整体自旋极化被抵消为零，此为“隐藏”之意。在能带上，根据空间反演对称性有ϵ↑n(k)=ϵ↑n(-k)，根据时间反演对称性有ϵ↓n(k)=ϵ↑n(-k) (Kramers简并)，两对称性联合(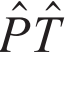)导致自旋简并，即ϵ↑n(k)=ϵ↓n(k)，故动量空间的自旋能带不发生劈裂。如图2(a)所示，中心反演对称的晶体材料LaOBiS2原胞中包含局域空间反演破缺的α和β两个原子层，其能带对应的布洛赫态可被投影至每个原子层而显现局域自旋极化，如图2(b)—(d)所示。由于加入了实空间原子层的自由度，这种局域自旋极化本质上是一种自旋—动量—层锁定(spin-momentum-layer locking)效应。值得注意的是，这里的动量指的是定义在布里渊区内的晶格动量，而具有确定晶格动量的电子布洛赫态中，电子出现在每个原胞中的概率相等，因此这种“动量—层锁定”与海森堡不确定性原理并不矛盾。

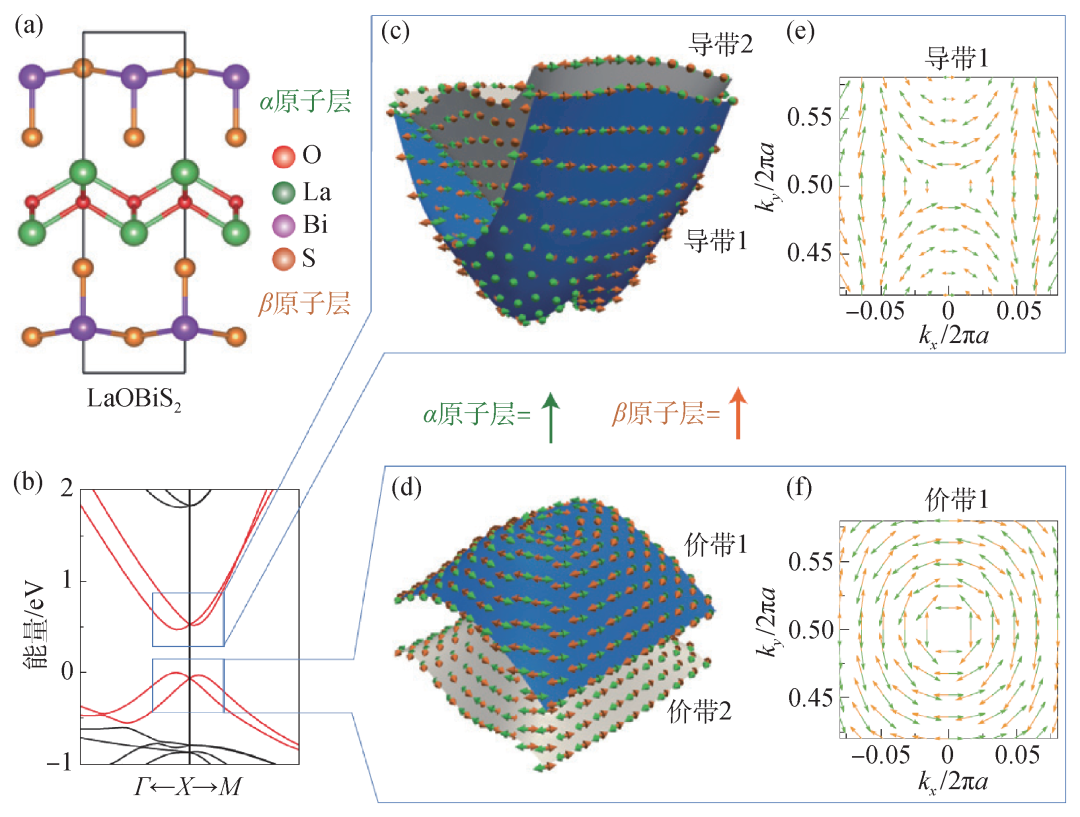
图2 LaOBiS2的隐藏自旋极化现象 (a)原子结构示意图，包括上下两个不同的BiS2原子层；(b)第一性原理计算能带结构图。其中每条能带由于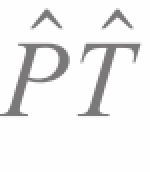对称均为二重简并，总自旋极化为零，但投影至每个原子层的局域自旋极化不为零，即隐藏自旋极化；(c，d)导带与价带的三维能带示意图，其中箭头标出了能带的局域自旋极化；(e，f)分别进一步展示了导带和价带的局域自旋极化二维投影图，可以看到，导带为Dresselhaus型，而价带为Rashba型隐藏自旋极化[9]   进一步研究发现，隐藏自旋极化的大小与空间反演联系的α和β层的电子波函数的杂化程度相关，当波函数在互为空间反演的两个原子之间杂化越强时，局域在层的自旋极化越小，反之亦然。例如单晶硅，尽管对称性分析表明隐藏自旋极化存在于不同的硅原子中，但是两个硅原子间的强杂化使得每个硅原子上的自旋极化非常弱以至于难以被探测。而对于一些具有非点式对称性的材料，布里渊区边界处的波函数由于对称性保护杂化强度为零，相应的隐藏自旋极化可达100%[11]。  

新概念的提出自然是创新的，然而其重要与否仍需等待实验验证以及进一步的应用来判断。对于非磁材料而言，隐藏自旋极化不仅在实空间上呈奇函数分布，在动量空间上亦呈奇函数分布。这使得直接探测变得棘手，目前仅有高精尖的自旋—角分辨光电子能谱(Spin-ARPES)技术能与之一试。当光电子从晶体表面射入时，能谱强度随着射入深度逐渐减弱，即互补的两局部自旋极化在能谱强度上大小不一，使得隐藏自旋极化得以呈现。2014年下半年，英国P. King课题组利用自旋角分辨光电子谱技术首次在三维WSe2块材中证实了强烈的隐藏自旋极化现象局域在每个单层上[12]；2017年清华大学周树云课题组运用同样的技术在二维PtSe2单层中也观测到了该现象[13]；2017年日本T. Okuda课题组在超导体LaO0.55F0.45BiS2中也找到了隐藏Rashba和Dresselhaus极化共存的实验证据[14]；2018年，美国A. Lanzara课题组在高温铜基超导体中也实验观测到隐藏极化现象[15]；2021年，笔者与合作者结合理论计算和能谱实验证实了BiIO材料中不同动量处完全迥异的自旋—动量—层锁定效应[16]。

然而，如此精细的测量方法难以推及到器件应用上。究其原因，正是材料的整体高对称性所保护的“隐藏”效果使得隐藏自旋极化难以被探测及应用。因此，人们首先想到施加外电场来打破整体空间反演对称性，再进一步构建器件。例如，基于隐藏自旋极化的自旋场效应晶体管[10]不同于前文所提到的基于Rashba效应的自旋场效应晶体管，后者是通过电场调控自旋轨道耦合作用的强度，而前者是通过电场分离隐藏自旋极化使其呈现，这通常能获得更好的电场调控效果。

另一方面，由于隐藏自旋极化是一个空间分布的奇函数，倘若材料中同时存在另一个空间奇分布的物理量能与前者耦合，奇奇得偶，那么一个空间偶函数分布从而整体积分不为零的宏观可观测量便可能存在。这个空间奇分布物理量可以是交错排列的反铁磁磁矩、反铁电极化，甚至特定波长的电磁波等等。据以上策略，我们课题组最近理论预言了隐藏自旋极化与反铁磁奈尔序相互耦合引起的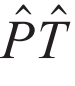—反铁磁非互易输运效应[17]。如图3所示，在反铁磁材料的每个子晶格中，沿正向和反向输运的载流子由于隐藏自旋极化效应，分别携带方向相反的自旋极化，因此被局域磁矩所散射的强度不同。这导致了沿正反两个方向的电导也是不同的，此即非互易输运。同时，由于载流子自旋极化与局域磁矩的共同反向，两个不同子晶格中的非互易电输运效果为叠加，而不是相消。当奈尔矢量翻转180°时，局域空间反演破缺所引起的隐藏自旋极化方向并不会发生变化，这使得非互易输运信号的符号翻转。因此，通过非线性输运测量，隐藏自旋极化也可被用于探测奈尔序。通过哈密顿模型分析，我们进一步发现隐藏自旋极化与奈尔序的耦合导致能带在相反动量上具有非对称特性，并利用推广的玻尔兹曼方程推导发现，在弛豫时间近似下的外禀二阶非线性电导与这种非对称特性关联。鉴于最近反铁磁非互易输运的研究热潮，笔者指出这里隐藏自旋极化引起的非互易输运为费米面所主导的非本征项，与贝里曲率偶极子导致的非本征项和贝里联络相关的本征项三者共同构成非互易输运的起源。  

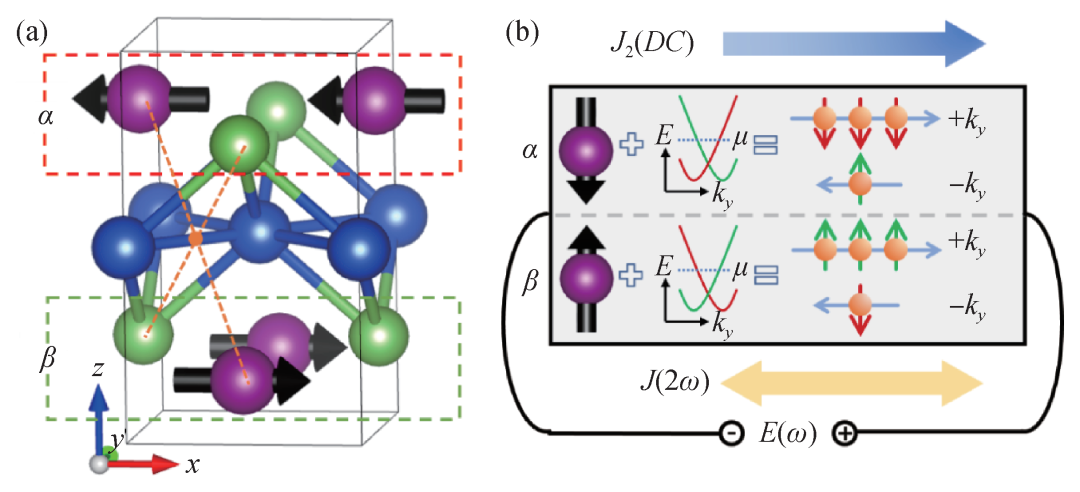
图3 (a)以CuMnAs为例的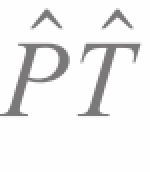—对称性反铁磁结构，互为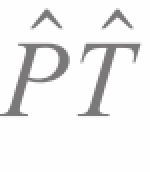反演的两原子层被标出；(b)反铁磁中隐藏自旋极化与奈尔序耦合引起非互易输运示意图，其中紫色球内黑箭头代表局域原子磁矩，能带与载流子(橙色小球)箭头的红绿色则表示了不同的局域自旋极化，在交变电场E(ω)下，两者耦合导致正向电流总大于反向电流，从而有单向直流J2(DC)，且有倍频交变电流J(2ω)，此即非互易输运[17]   说到反铁磁自旋电子学，我们不免想起反铁磁中局域自旋轨道力矩相关的里程碑工作，最早的理论文章发表于隐藏自旋极化被提出的同一年，即2014年[18]。局域自旋轨道力矩可用于电学翻转反铁磁奈尔矢量，其起源被归结为局域的自旋轨道耦合作用。然而，隐藏自旋极化与局域自旋轨道力矩的联系似乎更为直接和理所当然，即由自旋—动量—层锁定带来的局域自旋流直接对局域磁矩产生转移力矩。如此，通过调控隐藏自旋极化的强度，反铁磁自旋轨道力矩效应或许可进一步被优化。  

04 无自旋轨道耦合的自旋—动量锁定效应：反铁磁自旋极化

上文介绍了自旋轨道耦合作用产生的自旋—动量锁定效应，其中轨道自由度作为自旋和动量之间耦合的桥梁，发挥了重要作用。具体来说，在不考虑自旋轨道耦合时，电子在晶体中运动会受到各向异性晶体场的影响，自身轨道将和晶格动量产生耦合，即轨道—动量锁定。进一步考虑自旋轨道耦合，自旋通过和轨道的耦合进而和动量也产生锁定。因此，这种自旋—动量锁定实际上是自旋—轨道—动量锁定，是量子材料多自由度耦合带来的结果。

然而，在磁性材料中，自旋—动量锁定可以不依赖于自旋轨道耦合效应。这是因为局域磁矩的实空间分布S(r)产生的磁交换作用同样可以导致动量依赖的等效磁场Beff(k)。从对称性的观点出发，在忽略自旋轨道耦合时，非磁材料的自旋空间和实空间完全解耦。因此，自旋空间具有完整的SU(2)对称性，保护上下自旋在整个动量空间中处处二重简并。而对于磁性体系，实空间的局域磁矩和自旋的耦合S(r)∙σ破坏了自旋的SU(2)对称性，从而具备出现自旋劈裂的基本条件[19]。进一步，如果系统的晶格和磁结构也破坏了其他约束全动量空间自旋简并的对称性(如前文中提到的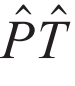对称性)，此时便会在无自旋轨道耦合的情况下出现自旋劈裂以及自旋—动量锁定效应。与非磁体系中自旋—动量锁定由晶体对称性决定不同，磁性体系局域磁矩产生的自旋—动量锁定强烈依赖于体系的磁结构S(r)。例如，铁磁体系中共线的局域磁矩产生同向磁场，可以引起全动量空间的Zeeman型自旋劈裂。在具有复杂磁结构的体系中，电子沿不同方向r运动时感受到S(r)带来的不同方向的有效磁场，因此会出现更丰富的自旋—动量锁定形式。有趣的是，这种由局域磁矩产生自旋—动量锁定的机制并不依赖于轨道的分布，因此比非磁体系中依赖自旋轨道耦合的机制更贴切“自旋—动量锁定”这一描述。

接下来，我们将重点介绍反铁磁中丰富的自旋劈裂现象。反铁磁具有多个局域磁矩互相补偿的子晶格，整体净磁矩为零。因此，长期以来反铁磁都被认为不具有自旋劈裂。然而，近期涌现出的一些研究表明，反铁磁中也可以存在较大的自旋劈裂，并且不需要自旋轨道耦合[20—22]。下面，我们以具有两个磁性子晶格的共线反铁磁为例，简要说明反铁磁中自旋劈裂的条件。和前文中非磁体系中的讨论类似，反铁磁的两个子晶格磁矩分别引起相反的局域自旋极化，因此当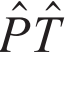对称性将两个子晶格联系起来时，有Pα(k)=-Pβ(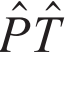k)=-Pβ(k)。此时两个子晶格的局域自旋极化在整个动量空间(布里渊区)处处相消。另一方面，联系两个子晶格的对称性除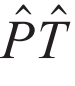外还可以是旋转联合时间反演等对称性。以4次旋转和时间反演的联合操作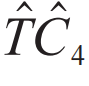为例(更确切地说，是自旋空间下自旋翻转180°的操作联合空间的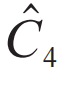旋转操作)，子晶格自旋极化满足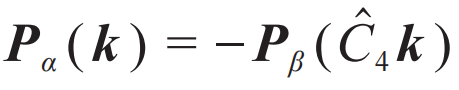。在动量空间内，仅有旋转轴等少数k点满足该对称性(即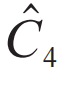k=k+R，R代表倒格矢)。因此，两个子晶格自旋极化并不在动量空间处处相消，而是形成动量依赖的自旋劈裂。MnF2、RuO2正是符合上述条件的共线反铁磁材料。在无自旋轨道耦合的情况下，自旋依然是好量子数，因此其能带劈裂为自旋向上和自旋向下两部分，在动量空间通过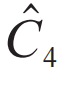对称性联系起来，如图4所示[22]。  

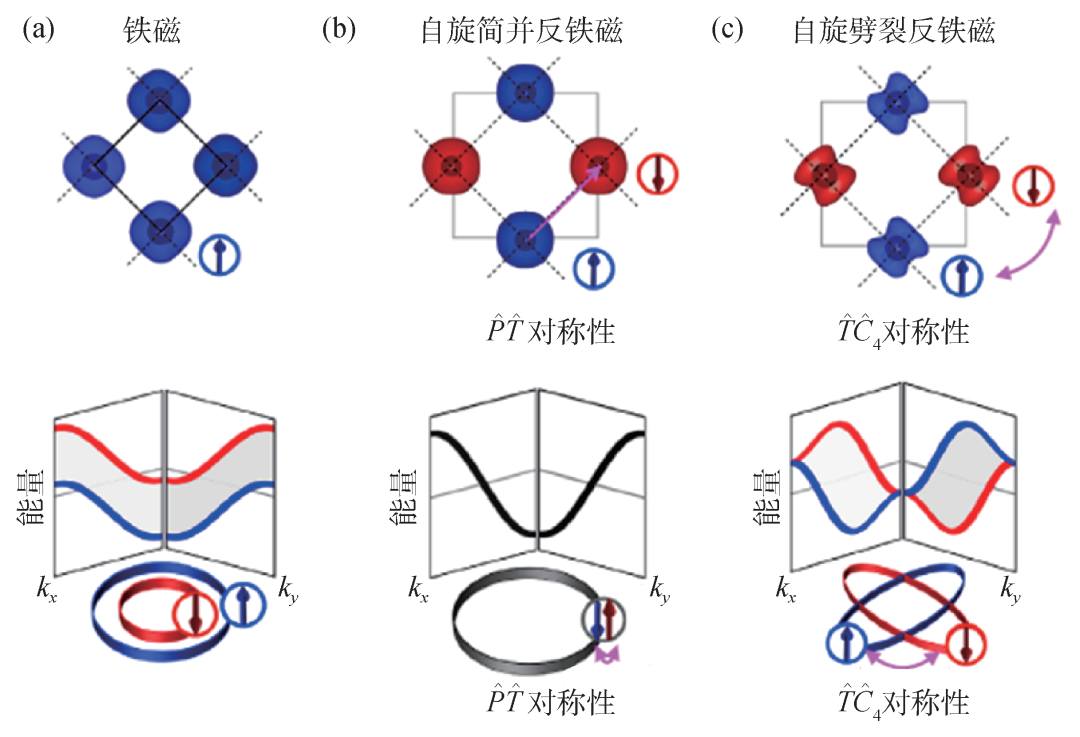
图4 共线磁体子晶格结构(上图)和自旋劈裂示意图(下图) (a)只有一个子晶格的铁磁体；(b)由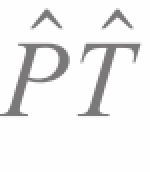对称性连接子晶格的自旋简并反铁磁体；(c)由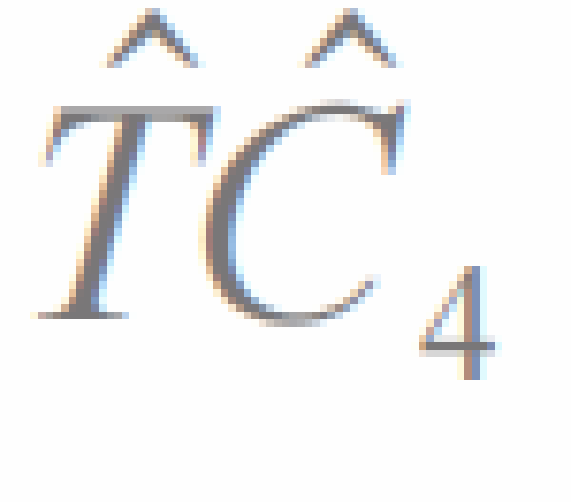



对称性连接子晶格的自旋劈裂反铁磁体。其中蓝色和红色分别代表自旋向上和自旋向下的子晶格/能带[22] 值得注意的是，上述反铁磁自旋劈裂都不需要自旋轨道耦合，因此描述自旋轨道耦合磁性体系的磁空间群无法完整描述上述体系的对称性。以具有笼目晶格的共面反铁磁Mn3Sn为例，其磁性原子由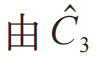对称性联系，即绕垂直笼目平面的旋转轴转动120°，但对应局域磁矩需要240°旋转，磁空间群中的旋转操作需要空间与自旋转动相同的角度，因此并不包含这类对称操作(空间旋转120°联合自旋旋转240°)。完整考虑如Mn3Sn等反铁磁体系的对称性及无自旋轨道耦合的电子结构需要使用更庞大的自旋空间群描述[19，23]，其理论研究最近也引起了广泛的关注。  

在实验上，对反铁磁自旋极化也可采用自旋—角分辨光电子能谱进行直接的谱学观测。2023年，我们与合作者利用该实验手段在非共面反铁磁MnTe2中首次直接观测到了反铁磁自旋极化[24]。另外，最近的研究将具有自旋劈裂的共线反铁磁相命名为交替磁性[22，25]，其自旋极化的费米面可以被外场调控，成为实现反铁磁自旋电子学的一个重要基础。基于反铁磁自旋极化，诸如自旋劈裂力矩、反铁磁隧穿磁电阻等新型自旋电子学效应也被相继提出和实验验证。图5展示了RuO2中自旋劈裂导致的自旋流。RuO2的费米面由自旋向上和自旋向下的两个椭圆形构成，彼此通过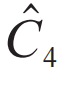对称性联系起来。对于一个自旋通道来说，其各向异性的椭圆形费米面可导致反常平面霍尔效应，即可产生横向电流以及横向自旋极化流。尽管该横向电流与另一个自旋通道上的反常平面霍尔电流相互抵消，横向自旋极化流却能彼此叠加，从而演化成所谓的自旋劈裂力矩[26，27]。另一方面，由于反铁磁自旋极化来源于磁交换作用，其自旋能带劈裂通常能达到1 eV，比自旋轨道耦合作用要大1—2个量级。故类比于铁磁金属/绝缘体/铁磁金属隧道结，反铁磁自旋极化金属/绝缘体/反铁磁自旋极化金属也有望产生可观的隧穿磁电阻效应。2022年，国内外学者相继理论提出和实验验证了Mn3Sn/绝缘体/Mn3Sn的反铁磁隧穿磁电阻效应[28，29]。目前，反铁磁自旋极化及其输运效应研究正如火如荼地开展，将为反铁磁自旋电子学打开新的大门。  

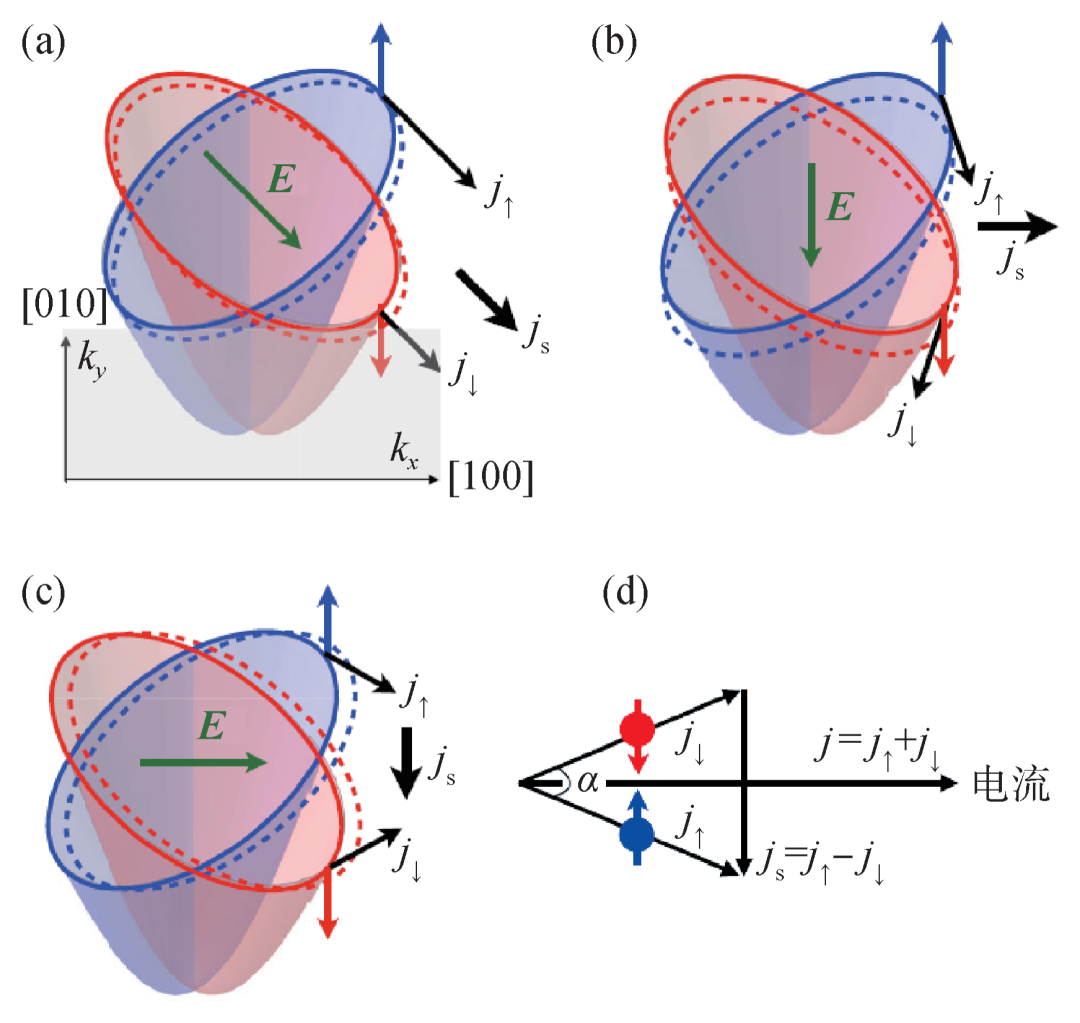
图5 (a—c)RuO2的费米面演示图以及不同外电场下的自旋流(js)示意图。(a)当电场E在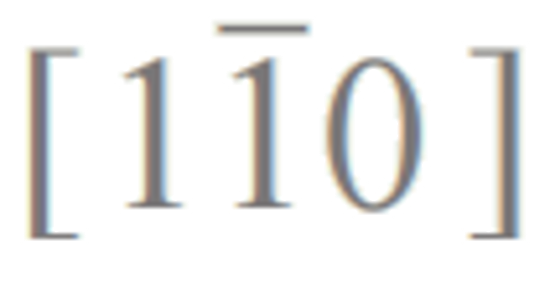方向时，仅有与E平行的纵向自旋流，而电场E为(b)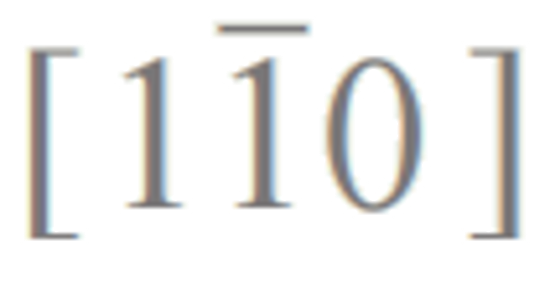方向或(c)[100]方向时，则有与E垂直的横向自旋流；(d)净横向自旋极化流示意图[26]

05 总结与展望

本文探讨了量子材料中由于多自由度耦合产生的自旋—动量锁定效应及其衍生的拓展效应，包括“隐藏自旋极化”和“反铁磁自旋极化”，以及相应的自旋电子学应用。其中，隐藏自旋极化由实空间互补的两套局域自旋极化组成，首先发现于整体空间反演对称但局部原子空间反演破缺的非磁晶体材料中，而后又被推广至具有对称性的反铁磁材料。前者起源于局域的自旋轨道耦合作用，而后者还包含了局域的磁交换作用。在(以及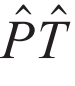加半周期平移)对称性破缺的反铁磁材料中，局域磁交换作用导致的局域自旋极化在动量空间上并非处处互补，在整体上形成动量空间依赖的自旋能带劈裂，此即为反铁磁自旋极化。最近，作为两个效应的结合，无自旋轨道耦合作用下的反铁磁隐藏自旋极化效应被预言[30]。  

接下来，我们展望相关领域仍存在的开放问题。首先，我们介绍了自旋—动量锁定效应的来源，并且讨论了轨道、实空间原子层等自由度的影响。然而如前文所述，对于真实材料中具体会出现哪种类型的自旋劈裂，自旋织构呈现什么形状尚无统一的微观机理。除提到的Zeeman型、Dresselhaus和Rashba型自旋劈裂以外，还存在Weyl型、三阶Rashba型、持续型(persistent)等多种自旋织构类型。另外，轨道和实空间原子自由度的引入也引起更多的新奇效应，这极大增加了耦合的复杂性。因此，一种可以描述上述完整自旋—动量—轨道—层锁定的普适理论是当下需要的。

例如，人们熟知的过渡金属硫族化合物中的能谷依赖的圆二色性构成了谷电子学的基础[31]，以及2013年张守晟团队预言的自旋轨道织构都是一种自旋—轨道—动量锁定效应[32]。最近，笔者从对称性的角度出发提出了可以全面描述自旋—动量—轨道—层锁定效应的理论[33]。通过使用轨道和原子位置的对称性表示矩阵构建k∙p哈密顿量模型，从而可以得到所有真实材料可能出现的自旋织构。这样一种通用理论可以对所有可能的自旋织构进行分类，还能够预测新的自旋—动量锁定效应，如动量二次型的自旋织构，反铁磁体中的Zeeman劈裂等。

其次，隐藏自旋极化理论可以衍生出一个更加广义的科学问题：具有宏观高对称性的体系能否实现那些低对称性允许的物理效应？答案是肯定的。这类物理效应在2014年之后被国际上不同研究团队从自旋极化推广到了其他受对称性约束的物理量，如轨道极化、光极化、贝里曲率，发展出了隐藏轨道极化[34]、隐藏光极化[35]、隐藏贝里曲率[36]等概念，逐步建成了“隐藏X物理”的小领域。最近的研究发现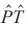，对称的反铁磁体系，如MnBi2Te4材料中存在逐层分辨的隐藏贝里曲率，可以在门电压的调控下产生层依赖的反常霍尔效应，被称为层霍尔效应[37，38]，与自旋霍尔效应、谷霍尔效应类似，成为霍尔效应家族中新的一员。此外，中心对称材料中也存在轨道自由度对应的轨道霍尔效应[39]。具有广泛意义的“隐藏X物理”及其新效应研究仍处于起步阶段，有待更多理论以及实验方面的研究。  

最后，反铁磁自旋极化导致的新效应最近成为自旋电子学最新发展的一个契机。由于净磁矩为零从而无杂散场，并且磁动力学过程为THz量级，反铁磁材料可用于实现高度集成和快速信息运算。然而，一般反铁磁材料的奈尔序难以被探测和操控，这使其无法成为理想信息载体。如今，反铁磁自旋极化的发现为反铁磁自旋电子学带来了全新的机会。例如反铁磁中性自旋流[40]、反铁磁隧穿磁电阻、巨磁电阻等效应可用于探测奈尔序[28，41]，而反铁磁自旋转移力矩、自旋劈裂力矩等可用于操控奈尔序[26，27]。另外，在这类反铁磁自旋极化材料中，人们还发现了反铁磁霍尔效应、非互易输运效应、手性磁振子等诸多新奇效应。其中，大部分效应处于发现的初步阶段，仍需进一步的理论计算和实验研究，从而有效发掘其巨大的应用潜力。

本文所阐述的新效应来源于量子材料中多自由度之间的耦合，如自旋—轨道—层、自旋—磁矩—轨道耦合等等，由此我们期待更多自由度的引入以及带来的新奇效应，这也是量子材料能够不断涌现新奇效应的独特魅力所在！






审核编辑：刘清