存储电路实现原理详解

在用电路实现加法之后，就需要一个能把结果保存下来的存储电路。设想存储电路的运行逻辑是：有一个控制开关，当着开关=1的时候，输出端等于输入端的值，当开关=0的时候，输入端的值的变化，不影响输出端的值，也就是输出端保持之前的数值。

4.1. 一位触发器

首先我们得承认，要像上一章的加法器一样，通过逻辑分析设计这样一个能满足存储数字需求的电路不是一件很容易的事情，本章拿前人的成果，直接把电路给出来，试着给大家分析。

1918年英国工程师埃克尔斯发明了一个具有记忆功能的电路，如图 4-1：

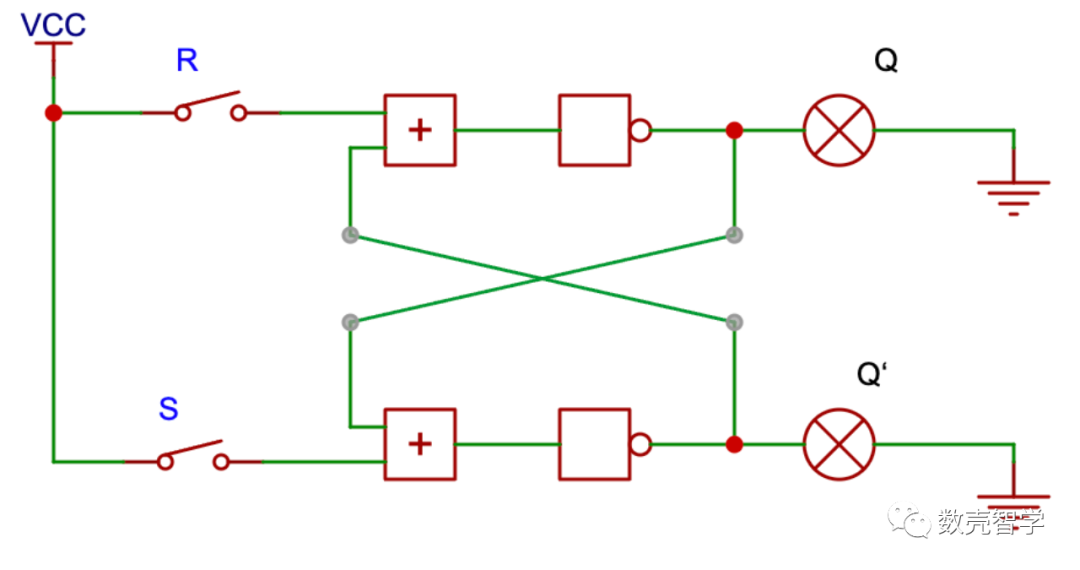
图 4-1具有记忆能力的电路（触发器）

这是一个震荡反馈电路，对于初学者来说稍微有点烧脑，我们列出这个电路的真值表（表 4-1）：

表 4-1 触发器的输入输出真值表

S	R	Q
0	0	不变	不变
0	1	0	1
1	0	1	0
1	1	0	0

我们可以发现该电路最神奇的地方在于当S=R=0的时候，可以保持输出的值Q不变，即这个时候Q的值不受R的变化影响，也就是Q能够保存一个比特的信号，这就是使得其具有作为存储电路的可能性。

仔细分析这个表的输入输出，可以发现几个有意思的特征可以被利用：

1、如果另S和R保持相反的输入（即R=0，S=1 或者R=1，S=0），则输出Q的值一直和R保持一致；

2、如果S=R=1，输出Q=0；S=R=0，输出Q保存一个比特信号；

在此技术上，我们稍微修改一下电路

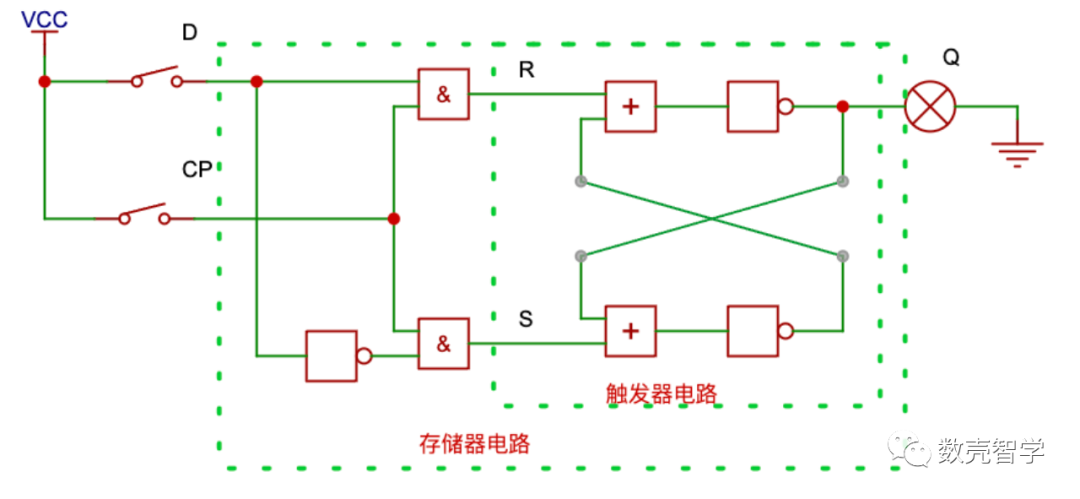
图 4-2一位寄存器比特单元电路

在图 4-1的基础上，在S、R两个输入端分别增加一个“与门”，用CP开关进行控制，根据表 4-1，电路逻辑状态如下：

当CP=0，无论开关D=0还是D=1，通过两个与门的作用，S=R=0，Q保持之前的值不变，起到保存比特信号的效果；

当CP=1，S、R的值取决于开关D的状态，D=1，则S=1、R=0、输出Q=D=1，相反D=0，则S=0、R=1、输出Q=D=0，也就是该状态下，存储器可以把输入的值写入到Q。

至此，一个完整的一位存储电路设计完成了，CP是状态控制开关，CP=1，使得输出Q=输入D；CP=0，输出状态不变，实现存储。

图 4-2是完整的一位存储电路，大虚线框代表的就是存储电路，用简化的图例可以表示为：

图 4-3触发器示意图

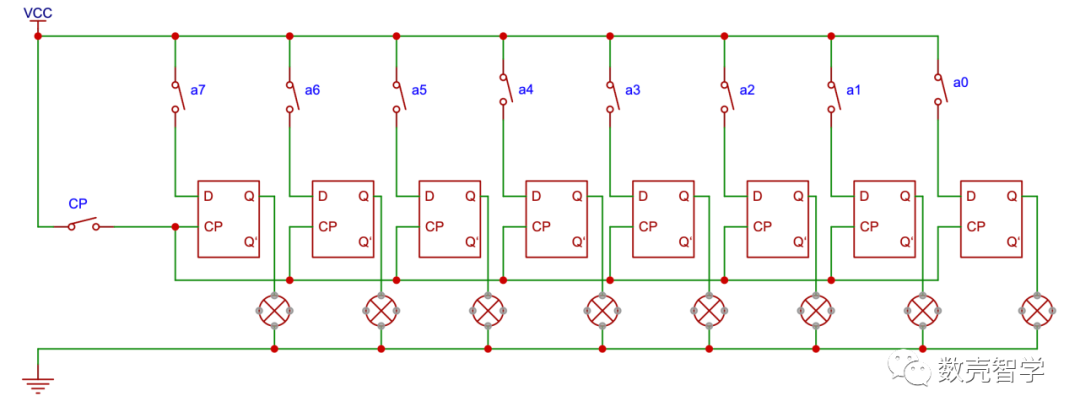
图 4-4 八位二进制数字存储

4.2. 存储芯片设计

图 4-2的电路输入、输出在不同的线路端，对于存储芯片的使用来说还是不够方便。作为存储芯片，我们希望写入和读取是同一个端口，用写入（W）、读取（R）两个控制端决定当前是处于读取还是写入状态，这样的设计更有利于大规模的存储电路的堆叠。

图 4-5 比特存储单元电路

图 4-5中把寄存器单元的输出Q和“读”控制开关R通过“与门”G连接，输出端和输入端D连接。当R断开状态，G与DB端的连线相当于断开，使得寄存器输出端Q不对DB端的状态造成影响。工作步骤如下：

1、W合并，R断开，写入状态：Q=DB

2、W断开，R断开，保持状态：Q不受DB影响；

3、W断开，R合并，读取状态：DB=Q

至此，我们完成存储芯片的比特单元的电路设计，用更简单的示意图表示如下：

图 4-6比特存储单元电路示意图

图 4-7 八位存储芯片单元（寄存器）电路图

现在我们已经可以尝试站在软件开发的角度对存储芯片的电路设计提一些需求，把图 4-7的8位整体作为一个字节的存储单元，一个存储芯片有大量的字节存储单元（比如现在主流的8G内存有810241024个这样的字节存储单元），希望给每个存储单元一个位置编号，方便在编程的时候直接定位存储的位置，这个位置编号成为“地址”。

图 4-7的简化示意图如下：

图 4-8 八位寄存器示意图

为了方便理解，先给出一个字节存储单元叠在一起的电路图（图 4-9）作为过度，从图中可以看出，默认状态所有的读、写控制都断开，当需要对第一行进行“存”操作，只需要把W0=1，该状态下D0～D7修改的值都会被保存到第一行的8个电路中。

图 4-9 四组八位存储芯片字节单元组电路图

这个电路与我们的存储芯片越来越接近了，但是还有一个缺点，每行都需要W、R两个控制端，那么一个保存256字节的存储芯片就有256*2个控制端，而且，随着存储芯片的容量越来越大，控制端越来越多，如果封装成一个芯片不可能设置那么多的针脚，所以必须想到变通的方法。

观察发现，虽然W、R控制端总数很多，但是在存储芯片操作的过程中，每次只会对其中的一行（一个字节）操作。我们需要一个地址选择功能的电路，通过输入n位的数字，能够实现在2^n^个地址中选中一个。因为n位的二进制数字能表示0～2^n-1^的数字，才提出这么精准的设计需求。

有一种叫“译码器”的电路逻辑，解决了这种问题。我们用一个2进4出的译码器电路来演示说明其原理，方法类似设计加法器电路（图 3-3）设计的方法：

1、列出所有可能的逻辑表达值（表 4-2）；

表 4-2 二进四出译码器逻辑真值表

A1	A0	D3	D2	D1	D0
0	0	0	0	0	1
0	1	0	0	1	0
1	0	0	1	0	0
1	1	1	0	0	0

2、根据真值表给出逻辑表达式；

3、根据逻辑表达式设计译码器的电路图

图 4-10 二进4出译码器电路图

三进八出译码器的示意图如下：

图 4-11三进八出译码器示意图

将译码器连接到字节单元组存储（图 4-9）的所有W、R端口（如图 4-12）。当A1=0，A0=1，通过译码器D1=1，W1通过与门连接D1和W（W1=D1&W），R1通过与门连接D1和R（R1=D1&R）。所以译码器控制了选中哪一行的存储单元，W、R实现对这行存储单元的读、写控制。

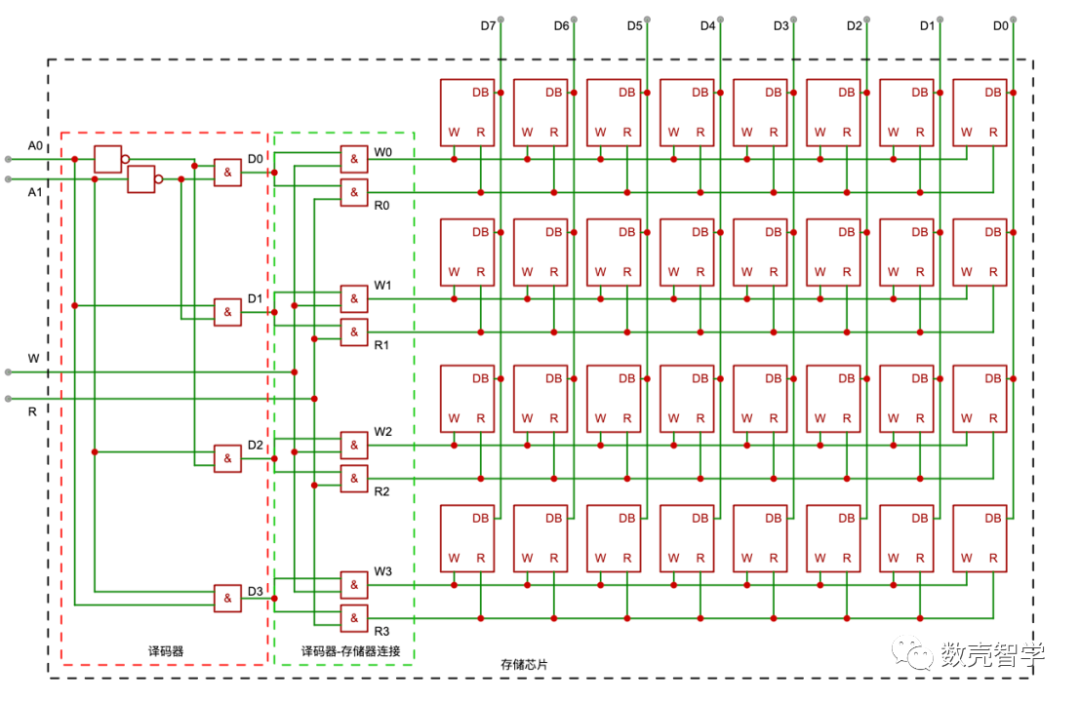
图 4-12连接译码器后的完整存储电路

图 4-12中利用2比特位的译码器实现了4行（4字节）的存储芯片，同理，可以用8比特位的译码器实现256行（256字节）的存储芯片。

这里的2比特位和8比特位即内存地址长度，现在计算机的操作系统常用32位和64位，指的就是内存的地址长度。按照这样的理解32位的操作，最长控制4294967296个地址，因为每个地址所代表的内存空间也是32位（4个字节），可以说其能控制的最大存储是：4294967296 * 4字节 = 16GB。当然现代计算机还可以通过译码器的级联扩展地址空间。

为了下文绘制电路图方便，把图 4-12简化成表示8位地址的内存示意图（图 4-13）：

图 4-13 八位地址的内存示意图