尽管基本PLL自其出现之日起几乎保持原样,但是使用不同技术制作及满足不同应用要求的PLL的实现一直给设计者提出挑战。
本篇先介绍一下传统电荷泵锁相环的稳定性和噪声建模,后续再从各种结构的PLL、电路设计注意事项、片上电感的设计等方面逐一展开。
1. PLL环路参数的计算及建模
**1.1 **环路参数的计算
传统电荷泵锁相环的结构框图如图1所示,由鉴频鉴相器(PFD)、电荷泵(CP)、环路滤波器(LPF)、压控振荡器(VCO)、分频器(1/N)组成。
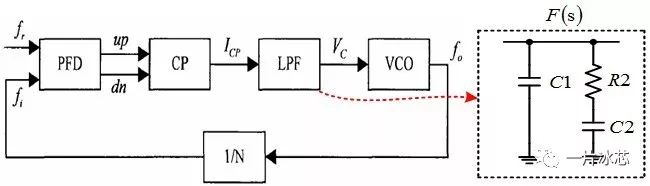
Fig1. 传统电荷泵 PLL结构框图
PLL设计指标:VDD=1.2V,Fref=25MHz,Fvco=1.25GHz,N=50。
第一步,确定VCO增益Kvco和CP充放电电流Icp。
按照20%的设计余量,将VCO的输出频率范围设定为1.0GHz到1.5GHz。在1.2V电源电压下为使CP电流源工作在饱和区,并考虑到为确保VCO增益的线性度而尽可能的压缩控制电压范围,将控制电压范围设为280mV到450mV,得Kvco≈3GHz/V。
实际设计时可适当增大控制电压范围(如200~1000mV),也可适当增大或减小Kvco,这里只是做一个假设,目的是学会如何计算PLL环路参数。
考虑面积功耗等因素的影响Icp折中取100uA。
第二步,环路带宽fc和相位裕度PM。
Fc取1MHz,PM取55deg。
将图1所示的PLL结构框图等效成图2所示的负反馈系统:

Fig2. PLL等效负反馈系统

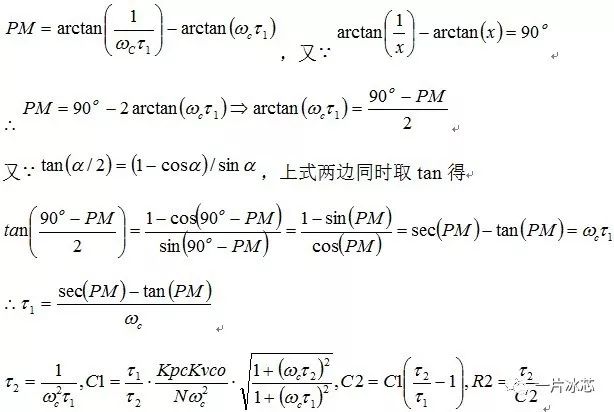
根据上述等式的推导,编写如下的MATLAB代码,可得滤波器的参数:
clear all;
close all;
clc;
Fc=1e6;%环路带宽
Kvco=2pi3e9;%VCO增益
Icp=100e-6;%电荷泵电流
Kpc=Icp/(2*pi);
N=50;%分频比
PM=55;%相位裕度
%==========================================================
Wc=2piFc;
fai=(pi/180)*PM;
tao1=(1/cos(fai)-tan(fai))/Wc;%时间常数1
tao2=1/(WcWctao1);%时间常数2
radnum=(Wc*tao2)^2+1;
radden=(Wc*tao1)^2+1;
a=sqrt(radnum/radden);
b=(KpcKvco)/(NWc*Wc);
C1=(tao1/tao2)ba;
C2=C1*(tao2/tao1-1);
R2=tao2/C2;
%=====================滤波器的传递函数======================
num1=[tao2,1];
den1=[tao1,1,0];
Fs=tf(num1,den1)/(C1+C2);
%=================整体开环L0s=Gs*Hs传递函数=================
G=KpcFsKvco;
den2=[1,0];
Gs=G*tf(1,den2);
Hs=1/N;
L0s=Gs*Hs;
%===================开环传递函数波特图======================
figure(1)
bode(L0s,{2pi10000,2pi100000000})
PLL幅频和相频特性曲线如图3所示,发现环路相位裕度和带宽与计算结果一致。

Fig3. PLL幅频和相频特性曲线
**1.2 **滤波器参数与环路带宽的关系
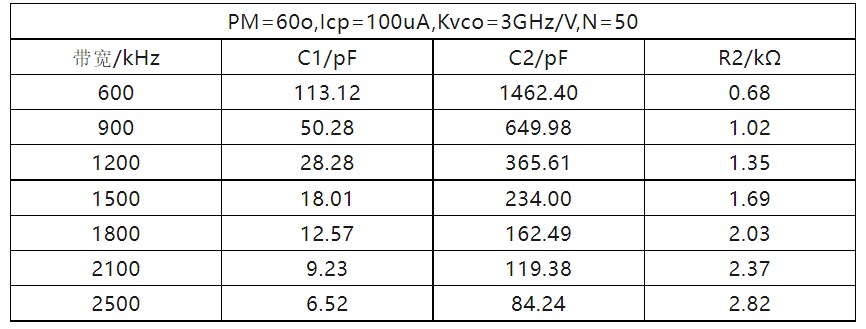
图4给出了PLL带宽与滤波器参数之间的关系

a. 环路带宽与C1的关系

b. 环路带宽与C2的关系
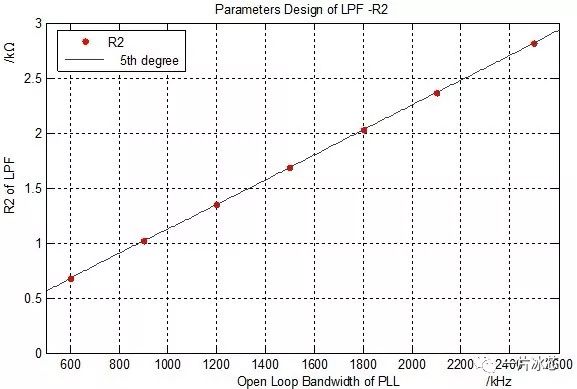
c. 环路带宽与R2的关系
Fig4. 环路带宽与滤波器参数的关系
结论:环路带宽与R2成正比,与C1和C2成反比
**1.3 **滤波器参数与相位裕度的关系

图5给出了PLL相位裕度与滤波器参数之间的关系

a. 相位裕度与C1的关系

b. 相位裕度与C2的关系
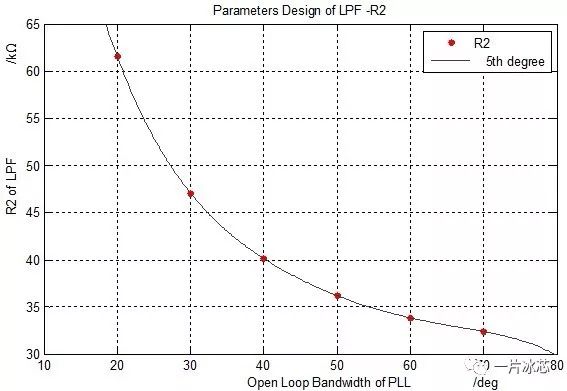
c. 相位裕度与R2的关系
Fig5. 相位裕度与滤波器参数的关系
结论:相位裕度与C2成正比,与C1和R2成反比
1.4 PLL****环路建模
用veriloga完成PLL建模,如图6所示。
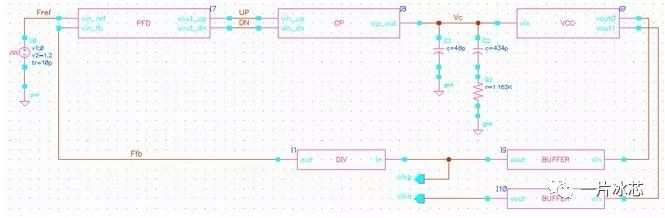
Fig6. PLL环路建模
用图6所示的环路模型可以做很多有意思的事情,图7和图8分别给出了锁定时间与环路带宽之间的关系,环路带宽/参考频率与稳定性之间的关系。下图7和图8说明:对于特定相位裕度,在一定范围内PLL锁定时间随带宽的增大不断减小,当带宽大于fref/10后系统的离散性变的越来越严重,带宽增大到fref/3后系统无法锁定。因此PLL环路带宽的选取存在一个折中,通常环路带宽取fref/20、fref/30或更小,具体多少要看应用。
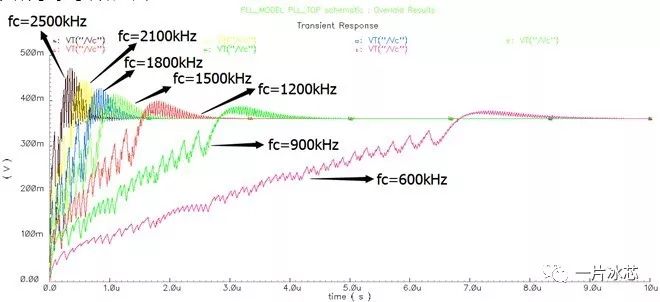
Fig7. 锁定时间与环路带宽之间的关系

Fig8. 环路带宽/参考频率与稳定性之间的关系
为了使PLL有最快的锁定时间,相位裕度也存在一个折中,由图9给出了相位裕度与稳定性之间的关系,可见相位裕度在50-70度之前是一个比较好的选择。

Fig9. 相位裕度与稳定性之间的关系
2. PLL噪声分析
**2.1 **噪声传函
图10给出了PLL相位域模型,并标注了各种噪声源。这些噪声源既包含了各模块的本征噪声,也包含了其他外部噪声源对本模块的影响,如电源电压噪声、衬底噪声等。可以得到该PLL的开环传递函数为:

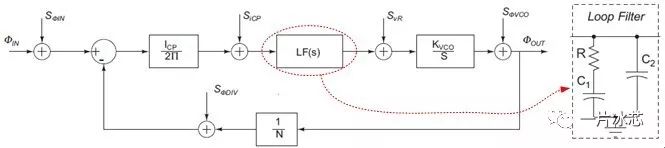
Fig10. PLL的相位域模型
由此可写出各模块到输出的噪声传递函数(NTF):

经上述分析可知,为了得到最佳的系统相位噪声性能,不仅要尽可能降低各个电路模块引入的噪声,而且还要合理选择环路带宽,有效地抑制带内和带外噪声。
PLL环路各参数选取如下:
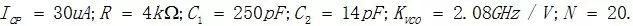
为得到参考时钟(Vref)到输出端(Vvco)的闭环噪声曲线,搭建了图11所示的PLL行为级模型,其中E0,E1调用analoglib里的vcvs(压控电压源);G0,G1调用analoglib里的vccs(压控电流源)。
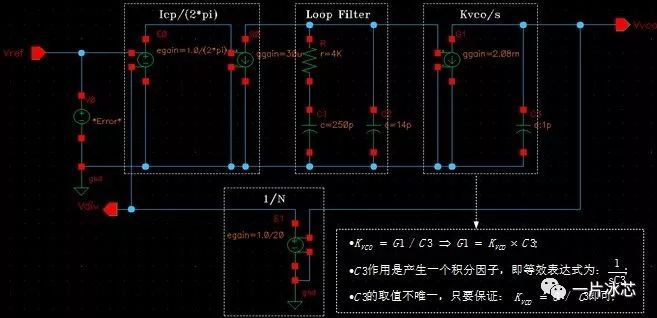
Fig11. 参考时钟到输出端的Test Bench
参考频率到输出端的闭环噪声传递函数具有低通特性。对图11建立的行为级模型进行AC仿真,得到其幅频特性如下图12所示,可见其具有低通特性,公式的正确性。

Fig12. 参考时钟到输出端的幅频特性曲线
同样搭建分频器到输出端的噪声仿真图,如图13所示:


Fig13. 分频器到输出端的Test Bench(上述两图均可)
分频器到输出端的幅频特性曲线,如图14所示:
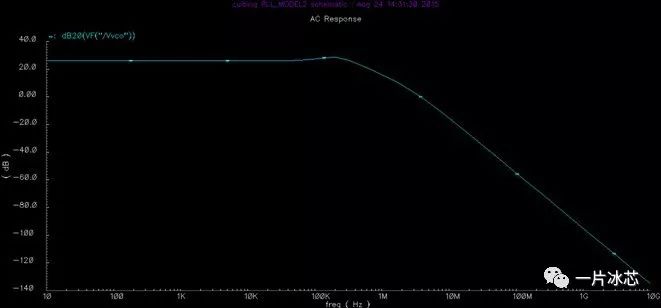
Fig14. 分频器到输出端的幅频特性曲线
同样搭建PFD到输出端的噪声仿真图,如图15所示:
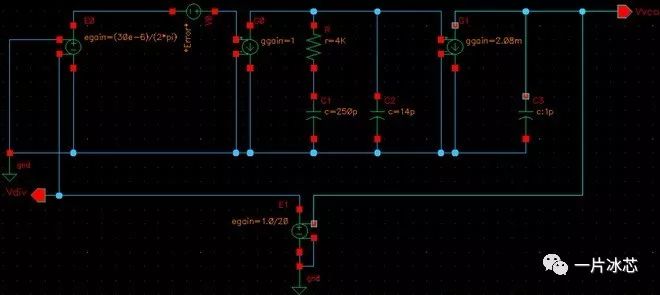
Fig15. PFD到输出端的Test Bench(对其做了简单等效)
PFD到输出端的幅频特性曲线,如图16所示:
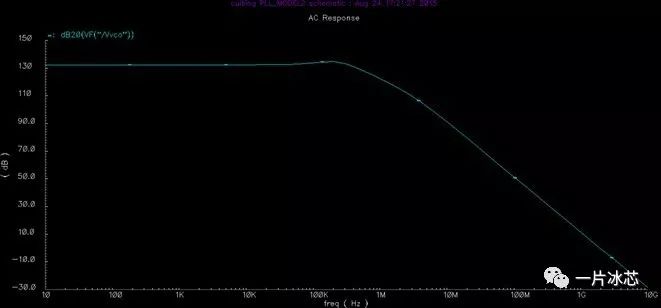
Fig16. PFD到输出端的幅频特性曲线
同样搭建环路滤波器到输出端的噪声仿真图,如图17所示:
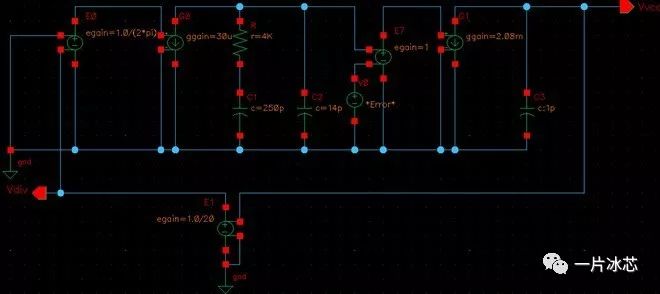
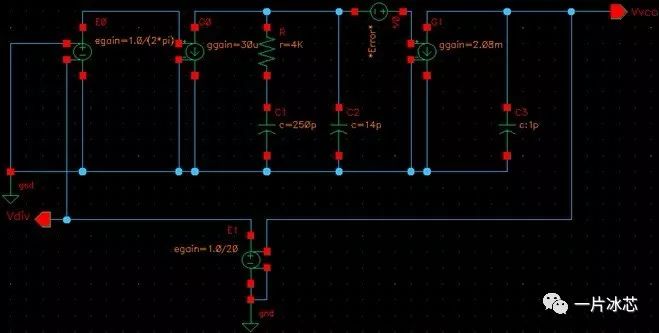
Fig17. 环路滤波器到输出端的Test Bench(上述两图均可)
环路滤波器到输出端的幅频特性曲线,如图18所示:

Fig18. 环路滤波器到输出端的幅频特性曲线
同样搭建VCO到输出端的噪声仿真图,如图19所示:
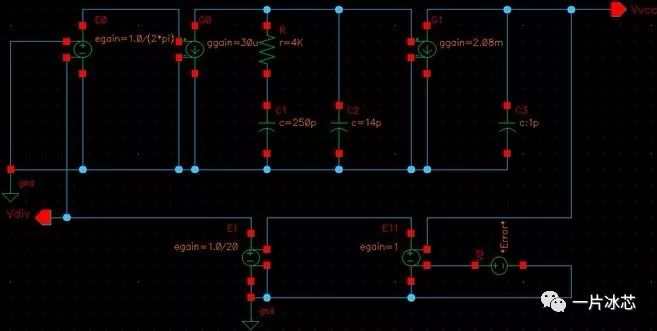

Fig19. VCO到输出端的Test Bench(上述两图均可)
VCO到输出端的幅频特性曲线,如图20所示:

Fig20. VCO到输出端的幅频特性曲线
同一坐标系下,PLL各噪声结点到输出端的幅频特性曲线如下图21所示:

Fig21. 同一坐标系下各噪声结点到输出端的幅频特性曲线
**2.2 **噪声建模
用veriloga完成了PLL噪声建模,如图22所示,验证qpll的噪声性能。模型采用传统电荷泵结构,各模块的噪声通过仿真或测试得到,所有噪声均转换为电压噪声(V ^2^ /Hz)。
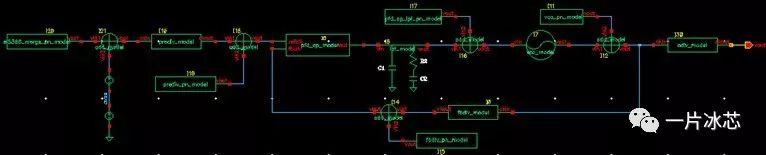
Fig22. PLL噪声建模
得到各模块电压噪声,进行noise仿真,得到输出端的电压噪声,然后用下式进行计算,得到Jitter:
spectre计算公式如下:

Rms_Jitter_Per_UI:(sqrt(integ(((getData("out"?result "noise")**2) * 2) 10 100000000 " ")) / 6.283185)
P2P_Jitter_Per_UI:((sqrt(integ(((getData("out"?result "noise")**2) * 2) 10 100000000 " ")) / 6.283185) *14)
output noise; V**2 / Hz:db((getData("out" ?result"noise")**2))
Total_PN:(10 * log10((getData("out"?result "noise")**2)))

Fig23. PLL noise拟合结果
上图环路16种仿真case下,输出噪声的rms jitter和p2p jitter统计如下:

tt corner下各模块噪声占比如图24所示:
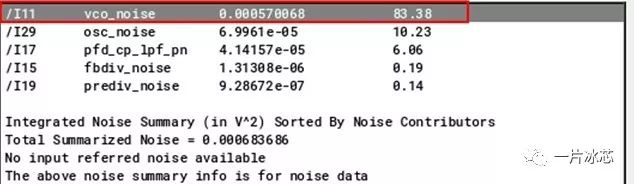
Fig24. 各模块的噪声占比
-
电荷泵
+关注
关注
3文章
239浏览量
29621 -
压控振荡器
+关注
关注
10文章
133浏览量
29337 -
VDD
+关注
关注
1文章
312浏览量
33326 -
鉴频鉴相器
+关注
关注
1文章
11浏览量
11307 -
PLL电路
+关注
关注
0文章
92浏览量
6431
发布评论请先 登录
相关推荐
请问怎么计算与AD9858片内PLL结合使用的环路滤波器参数?
pll环路滤波器计算
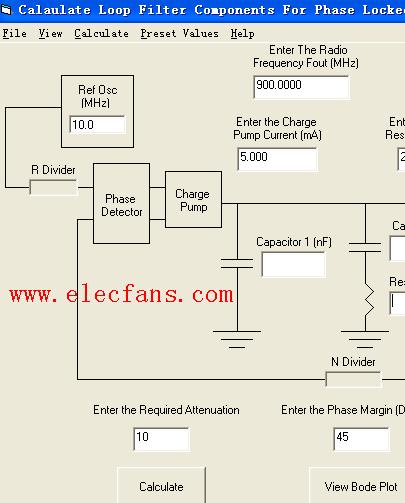
PLL频率合成器的主要构建模块详细资料说明
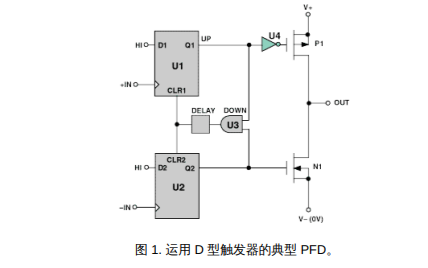




 PLL环路参数的计算及建模
PLL环路参数的计算及建模











评论