我准备使用scikit-learn给大家介绍一些模型的基础知识,今天就来讲讲 线性回归模型 。
1.准备
开始之前,你要确保Python和pip已经成功安装在电脑上,如果没有,可以访问这篇文章:超详细Python安装指南 进行安装。
**(可选1) **如果你用Python的目的是数据分析,可以直接安装Anaconda:Python数据分析与挖掘好帮手—Anaconda,它内置了Python和pip.
**(可选2) **此外,推荐大家用VSCode编辑器,它有许多的优点:Python 编程的最好搭档—VSCode 详细指南。
请选择以下任一种方式输入命令安装依赖 :
- Windows 环境 打开 Cmd (开始-运行-CMD)。
- MacOS 环境 打开 Terminal (command+空格输入Terminal)。
- 如果你用的是 VSCode编辑器 或 Pycharm,可以直接使用界面下方的Terminal.
pip install scikit-learn
2.简单的训练集
冬天快到了,深圳这几天已经准备开始入冬了。
从生活入手,外界温度对是否穿外套的影响是具有线性关系的:
| 外界温度 | 是否穿外套 |
|---|---|
| 30度 | 不 |
| 25度 | 不 |
| 20度 | 不 |
| 15度 | 是 |
| 10度 | 是 |
现在,考虑这样的一个问题:如果深圳的温度是12度,我们应不应该穿外套?
这个问题很简单,上述简单的训练集中,我们甚至不需要机器学习就能轻易地得到答案:应该。但如果训练集变得稍显复杂一些呢:

你能看出其中x1, x2, x3和y之间的规律吗?
比较难,但是如果你有足够的数据(比如100个),机器学习能够迅速解决这个问题。
为了方便展示机器学习的威力,我们在这里生产100个这样的训练集(公式为: y=x1 + 2x2 + 3x3):
from random import randint
TRAIN_SET_LIMIT = 1000
TRAIN_SET_COUNT = 100
TRAIN_INPUT = list()
TRAIN_OUTPUT = list()
for i in range(TRAIN_SET_COUNT):
a = randint(0, TRAIN_SET_LIMIT)
b = randint(0, TRAIN_SET_LIMIT)
c = randint(0, TRAIN_SET_LIMIT)
op = a + (2*b) + (3*c)
TRAIN_INPUT.append([a, b, c])
TRAIN_OUTPUT.append(op)
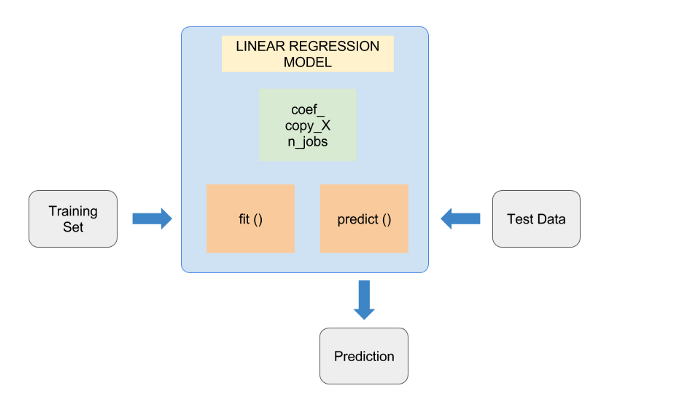
然后让线性回归模型使用该训练集(Training Set)进行训练(fit),然后再给定三个参数(Test Data),进行预测(predict),让它得到y值(Prediction),如下图所示。

3.训练和测试
为什么我使用sklearn?因为它真的真的很方便。像这样的训练行为,你只需要3行代码就能搞定:
from sklearn.linear_model import LinearRegression
predictor = LinearRegression(n_jobs=-1)
predictor.fit(X=TRAIN_INPUT, y=TRAIN_OUTPUT)
需要注意线性回归模型(LinearRegression)的参数:
n_jobs:默认为1,表示使用CPU的个数。当-1时,代表使用全部CPU
predictor.fit 即训练模型,X是我们在生成训练集时的TRAIN_INPUT,Y即TRAIN_OUTPUT.
训练完就可以立即进行测试了,调用predict函数即可:
X_TEST = [[10, 20, 30]]
outcome = predictor.predict(X=X_TEST)
coefficients = predictor.coef_
print('Outcome : {}nCoefficients : {}'.format(outcome, coefficients))
这里的 coefficients 是指系数,即x1, x2, x3.
得到的结果如下:
Outcome : [ 140.]
Coefficients : [ 1. 2. 3.]
验证一下:10 + 202 + 303 = 140 完全正确。
如何,机器学习模型,用起来其实真的没你想象中的那么难,大部分人很可能只是卡在了安装 scikit-learn 的路上...
顺便给大家留个小练习,将下列欧式距离,使用线性回归模型进行表示。

解决思路和本文的方案其实是类似的,只不过需要变通一下。
-
WINDOWS
+关注
关注
4文章
3551浏览量
88918 -
模型
+关注
关注
1文章
3268浏览量
48927 -
编辑器
+关注
关注
1文章
806浏览量
31211 -
python
+关注
关注
56文章
4800浏览量
84820 -
线性回归
+关注
关注
0文章
41浏览量
4310
发布评论请先 登录
相关推荐
TensorFlow实现简单线性回归
TensorFlow实现多元线性回归(超详细)
使用PyMC3包实现贝叶斯线性回归
基于Weierstrass逼近定理在非线性回归模型中应用
非线性GaN模型的基础知识和基础设计




 线性回归模型的基础知识
线性回归模型的基础知识


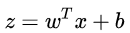










评论