SymPy 是一个Python库,专注于符号数学,它的目标是成为一个全功能的计算机代数系统,同时保持代码简洁、易于理解和扩展。
举一个简单的例子,比如说展开二次方程:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = ((x+y)**2).expand()
print(d)
# 结果:x**2 + 2*x*y + y**2
你可以随便输入表达式,即便是十次方,它都能轻易的展开,非常方便:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = ((x+y)**10).expand()
print(d)
# 结果:x**10 + 10*x**9*y + 45*x**8*y**2 + 120*x**7*y**3 + 210*x**6*y**4 + 252*x**5*y**5 + 210*x**4*y**6 + 120*x**3*y**7 + 45*x**2*y**8 + 10*x*y**9 + y**10
下面就来讲讲这个模块的具体使用方法和例子。
1.准备
开始之前,你要确保Python和pip已经成功安装在电脑上,如果没有,可以访问这篇文章:超详细Python安装指南 进行安装。
**(可选1) **如果你用Python的目的是数据分析,可以直接安装Anaconda:Python数据分析与挖掘好帮手—Anaconda,它内置了Python和pip.
**(可选2) **此外,推荐大家用VSCode编辑器,它有许多的优点:Python 编程的最好搭档—VSCode 详细指南。
请选择以下任一种方式输入命令安装依赖 :
- Windows 环境 打开 Cmd (开始-运行-CMD)。
- MacOS 环境 打开 Terminal (command+空格输入Terminal)。
- 如果你用的是 VSCode编辑器 或 Pycharm,可以直接使用界面下方的Terminal.
pip install Sympy
2.基本使用
简化表达式(化简)
sympy支持三种化简方式,分别是普通化简、三角化简、指数化简。
普通化简 simplify( ):
from sympy import *
x = Symbol('x')
d = simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))
print(d)
# 结果:x - 1
三角化简 trigsimp( ):
from sympy import *
x = Symbol('x')
d = trigsimp(sin(x)/cos(x))
print(d)
# 结果:tan(x)
指数化简 powsimp( ):
from sympy import *
x = Symbol('x')
a = Symbol('a')
b = Symbol('b')
d = powsimp(x**a*x**b)
print(d)
# 结果:x**(a + b)
解方程 solve()
第一个参数为要解的方程,要求右端等于0,第二个参数为要解的未知数。
如一元一次方程:
from sympy import *
x = Symbol('x')
d = solve(x * 3 - 6, x)
print(d)
# 结果:[2]
二元一次方程:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = solve([2 * x - y - 3, 3 * x + y - 7],[x, y])
print(d)
# 结果:{x: 2, y: 1}
求极限 limit()
dir=’+’表示求解右极限,dir=’-‘表示求解左极限:
from sympy import *
x = Symbol('x')
d = limit(1/x,x,oo,dir='+')
print(d)
# 结果:0
d = limit(1/x,x,oo,dir='-')
print(d)
# 结果:0
求积分 integrate( )
先试试求解不定积分:
from sympy import *
x = Symbol('x')
d = integrate(sin(x),x)
print(d)
# 结果:-cos(x)
再试试定积分:
from sympy import *
x = Symbol('x')
d = integrate(sin(x),(x,0,pi/2))
print(d)
# 结果:1
求导 diff()
使用 diff 函数可以对方程进行求导:
from sympy import *
x = Symbol('x')
d = diff(x**3,x)
print(d)
# 结果:3*x**2
d = diff(x**3,x,2)
print(d)
# 结果:6*x
解微分方程 dsolve( )
以 y′=2xy 为例:
from sympy import *
x = Symbol('x')
f = Function('f')
d = dsolve(diff(f(x),x) - 2*f(x)*x,f(x))
print(d)
# 结果:Eq(f(x), C1*exp(x**2))
3.实战一下
今天群里有同学问了这个问题,“大佬们,我想问问,如果这个积分用Python应该怎么写呢,谢谢大家”:
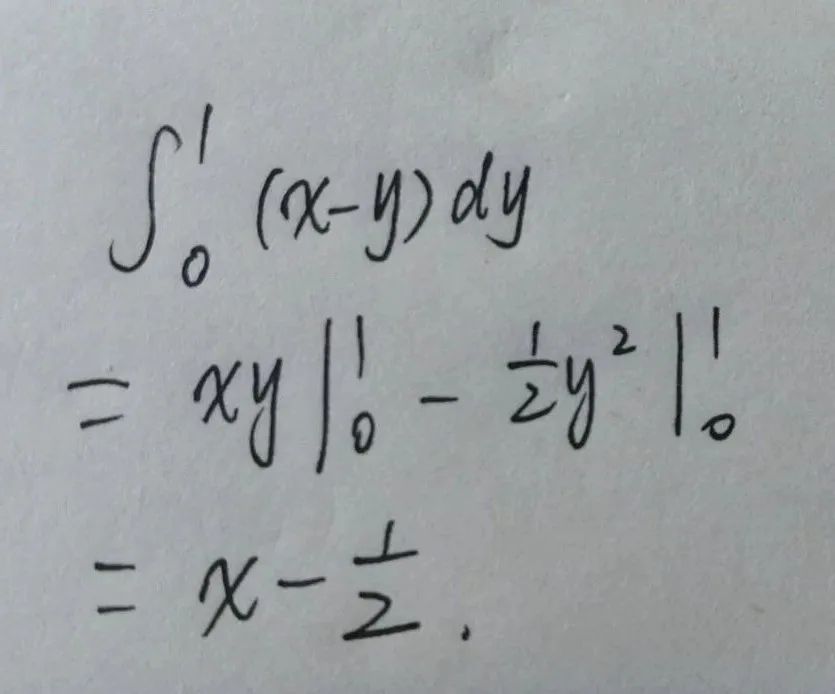
# Python 实用宝典
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = integrate(x-y, (y, 0, 1))
print(d)
# 结果:x - 1/2
为了计算这个结果,integrate的第一个参数是公式,第二个参数是积分变量及积分范围下标和上标。
运行后得到的结果便是 x - 1/2 与预期一致。
如果大家也有求解微积分、复杂方程的需要,可以试试sympy,它几乎是完美的存在。
-
模块
+关注
关注
7文章
2696浏览量
47438 -
计算机
+关注
关注
19文章
7489浏览量
87877
发布评论请先 登录
相关推荐
matlab数学建模工具箱
如何用Labview解复杂的数学方程?
分享《Matlab与微积分》课件
RC微积分电路的Multisim仿真
MATLAB教程之如何使用MATLAB求解数学问题资料概述
深度解读你也能懂的微积分
硬件设计为何还要学习微积分?
Banach空间几类分数阶微积分方程的mild解的存在性

戴维·M. 布雷苏:对微积分的思考
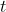
SymPy:四行代码秒解微积分




 Sympy模块如何解数学方程解微积分
Sympy模块如何解数学方程解微积分











评论