计算电磁学与仿真软件

1. 电磁算法简介

计算电磁学已成为解决复杂电磁工程问题最有效的方法之一。现有的电磁场数值方法主要分为：高频近似方法、全波数值方法及混合方法。

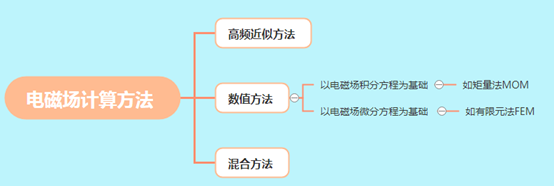
高频近似方法主要包括基于“场近似”的几何光学法（Geometrical Optics，Go）、几何绕射理论（Geometrical Theory of Diffraction，GTD）、一致性绕射法（Uniform Geometrical Theory of Diffraction，UTD）等和基于“源近似”的物理光学法（Physical Optics，PO）、物理绕射理论（Physical Theory of Diffraction，PTD）、弹跳射线法（Shooting Bouncing Ray Method，SBR）等。使用高频近似方法时无需存储矩阵，且其具有计算时间短、内存消耗低、计算效率高等优点，但是高频近似条件的引入，未完全考虑目标不同区域间的互耦，导致计算精度较低。因而，高频近似方法一般更适合于频率较高、目标电尺寸较大且界面光滑的电磁问题，而对于复杂目标，其求解精度通常难以满足工程要求。

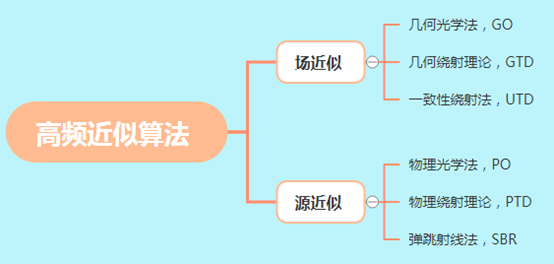
全波数值方法又被称之为低频方法，相较于解析法和近似方法，其优势为在计算资源允许的情况下，可以精确地分析任意非规则目标的电磁特性，并且能够求解任何频率的电磁问题。依据Maxwell方程组的不同形式，全波数值方法主要分为微分方程法和积分方程法。

常用的微分方程法有时域有限差分法（Finite Difference Time Domain，FDTD）和有限元法（Finite Element Method，FEM）两类。FDTD和FEM的优点在于算法生成的矩阵为稀疏矩阵，且易于处理有限尺寸下的含非均匀介质结构的复杂电磁问题。但对于开域问题，FDTD和FEM需设置吸收边界条件，还要设置足够的空间以满足截断边界条件，这种处理方式会带来截断误差和网格的色散误差，因而难以确保计算精度且额外的求解区域也导致了更大的计算量。

积分方程方法主要是矩量法（Method of moments，MoM）。采用MoM求解积分方程时，由于其所建立的格林函数自动满足Sommerfeld辐射条件，因此不会因为网格的离散而产生色散误差，进而具有较高的计算精度。同时，无需像微分方程法那样设置吸收边界条件，其待求未知量只位于散射体表面或者体内，从而大大减少了未知量，因此积分方程MoM法计算电磁辐射和散射问题具有较大优势。总的来说，矩量法是以电磁场积分方程为基础的数值方法，是一种严格的数值方法，其精度主要取决于目标几何建模精度、正确的基、权函数选择以及阻抗元素的计算。

2. 矩量法

1968年，Roger F.Harrington提出矩量法。

矩量法只需要离散几何模型而无须离散空间，无需设置边界条件，其计算量只取决于计算频率及模型的几何尺寸。矩量法是将算子方程化为矩阵方程，然后求解该矩阵方程。用矩量法求解电磁场问题的优点是严格地计算各子散射体间的互耦。

3. 有限元法

有限元（FEM）方法能够对复杂几何形状以及复杂非均匀介质目标进行模拟。

有限元法分析边值问题的基本步骤可归纳为：区域的离散或子域划分；插值函数的选择；方程组的建立；方程组的求解。

有限元法适用于处理非均匀介质或介质与金属的组合结构、微带结构以及填充非均匀介质或各向异性介质的波导问题。但是，该方法同时域有限差分法一样，难以处理开放区域的辐射与散射问题。在计算中，由于计算机内存的限制同样需要引入吸收边界条件，如完全匹配层（PML），进行网格截断。

4. 时域有限差分法

时域有限差分法（FDTD）适合宽频带电磁问题分析，如宽带天线和电磁屏蔽效能、雷击等应用。

1966年，K.S.Yee首次提出该电磁场计算新方法—FDTD。FDTD方法用于求解微分形式的麦克斯韦旋度方程组，利用差分原理将旋度方程组离散成为一组时域递推公式。它是一种时域直接求解法，随着时间的推进可以很方便地知道电磁场随时间的变化过程。

5. 物理光学法

物理光学（Physical Optics）方法是一种基于表面电流的方法，它应用积分方程的表达形式，并且遵循物理上合理的高频假设，即由物体上某一点对物体其他点的散射场的贡献和入射场相比是很小的，因此表面上每一点的总场公式可合理简化。

应用物理光学方法要求给定几何结构和入射场。目标表面的总场大小由入射电场决定，当电磁波入射到散射体面上时，有的区域能被电磁波照射到，有的区域却照射不到，被照射区域称为亮区，亮区的总场为非零，而照射不到的暗区的总场为零，这是物理光学法的主要缺点之一。

该方法的另一个主要缺陷是没有考虑散射体上的边缘，尖劈等不连续处所产生的电流对散射的贡献，故其计算结果在发射方向的近轴方向才有较好的计算精度，而在大角度辐射区的计算结果偏差较大。

物理光学理论通过对感应场的近似积分得到空间场，入射波照射到目标体表面，在表面亮区产生感应电流。采用物理光学方法能快速地计算电大尺寸目标体的特性，而且结果的精度可以满足工程需要。物理光学积分是在非封闭的表面亮区单元上进行的，目标表面暗区一侧的场为零。

6. 常用电磁仿真软件

Ansys HFSS 是一款 3D 电磁仿真软件，可用于设计天线、天线阵列、RF 或微波组件、高速互连装置、过滤器、连接器、IC 封装和印刷电路板等高频电子产品，并对此类产品进行仿真。HFSS是基于有限元法（FEM）的仿真器，适合仿真三维复杂结构，但是电长度要较小。

CST软件：CST工作室套装是面向3D电磁、电路、温度和结构应力设计工程师的一款全面、精确、集成度极高的专业仿真软件包。包含八个工作室子软件，集成在同一用户界面内，为用户提供完整的系统级和部件级的数值仿真优化。软件覆盖整个电磁频段，提供完备的时域和频域全波电磁算法和高频算法。典型应用包含电磁兼容、天线/RCS、高速互连SI/EMI/PI/眼图、手机、核磁共振、电真空管、粒子加速器、高功率微波、非线性光学、电气、场路、电磁-温度及温度-形变等各类协同仿真。CST是基于FDTD（时域有限差分法）电磁场求解算法的仿真器，适合仿真宽带频谱结果，因为只需要输入一个时域脉冲就可以覆盖宽频带。

AdvancedDesign System，是Agilent公司推出的微波电路和通信系统仿真软件。可实现包括时域和频域、数字与模拟、线性与非线性、噪声等多种仿真分析手段，并可对设计结果进行成品率分析与优化，从而大大提高了复杂电路的设计效率，是非常优秀的微波电路、系统信号链路的设计工具。主要应用于：射频和微波电路的设计，通信系统的设计，DSP设计和向量仿真。ADS内含矩量法（MOM），非常适合仿真第三维度上均匀变化的结构，例如电路多层板，如PCB，陶瓷等电路板，常见无源电路，如滤波器等结构。

FEKO电磁仿真软件：是第一个把矩量法（MoM）推向市场的商业软件。该方法使得精确分析电大问题成为可能。FEKO从严格的电磁场积分方程出发，以经典的矩量法(MOM)为基础，采用了多层快速多级子(MLFMM：Multi-Level Fast Multipole Method)算法在保持精度的前提下大大提高了计算效率，并将矩量法与经典的高频分析方法(物理光学PO：Physical Optics，一致性绕射理论UTD：Uniform Theory of Diffraction)无缝结合，从而非常适合于分析天线设计、雷达散射截面(RCS)、开域辐射、电磁兼容中的各类电磁场分析问题。

审核编辑：汤梓红