如何利用高斯过程回归模型建立燃料电池电堆功率预测模型？

摘要

对车辆辅助装置的控件进行优化设计时，需要建立一个燃料电池电堆功率预测模型，而该模型的建立需要考虑各种电堆控制参数，这一点至关重要。然而，创建一个可以定量预测电池电堆功率的模型需要用到大量的关于燃料电池内部材料和结构的数据。此外，由于模型内部存在各种复杂现象，需要进行大规模建模。在本研究中，我们采用空间填充技术这一实验设计方法有效获取了各项数据。基于获取的数据，我们利用高斯过程回归模型创建了一个能够在短时间内预测电堆性能以及电堆各部分温度和压力的模型。该模型可以用来计算最大化电堆功率所需的操作条件。除此之外，经试验证明，利用该功率预测模型还可以在有限的试验数据条件下研究电池电堆性能。

一

引言

1.1. 背景

聚合物电解质燃料电池（FC）以氢气（H₂）作为燃料，将化学能直接转化为电能。这就使其能源效率比内燃机更高，且运行过程中排放的只有水。因此，它是一种对环境影响较小的发电装置，有望广泛应用于汽车和卡车等领域，还可以用作工厂的备用电源（1）。特别是在汽车行业，各个国家都制定了相关的法律法规，寻求一款对环境影响较小的燃料电池汽车，作为实现电气化的一种方式。然而，由于基础设施建设不足、燃料电池电堆成本过高等多种原因，燃料电池汽车的普及率较低（2）、（3）。降低燃料电池电堆成本需要在有限的催化剂用量和活性面积的前提下达到必要的功率和耐用性（3）。因此，通过开发新材料和优化控制来提高功率输出是非常必要的。

燃料电池电堆内部的电流分布和电化学反应活性会根据发电环境中产生的气体、温度和水的变化而变化，电堆性能也会随之而发生变化。对此，我们进行了多项研究，通过数学建模再现堆栈内部环境，以预测电堆性能随各个控制变量的变化（4）、（5）。由于各参数间的相互影响，燃料电池电堆的数学建模十分复杂。需要掌握所涉及的各种物理现象的理论公式、各种材料的物理性质等等（6）。因此，一旦材料或燃料电池的结构发生变化，就要重新精确测量和系数拟合，以获得需要的参数。

随着人工智能技术的发展，越来越多的研究都开始利用机器学习来建模（7）。通过机器学习进行电堆性能建模的优点包括，可以在不进行仿真的情况下为电池电堆内部的复杂流体状态建模。

监督学习是机器学习的一种。可以通过适当地标记测量数据中特征值的输入和输出来获得相应的数据并创建模型。人工神经网络属于机器学习中的监督学习。使用人工神经网络的电堆功率预测模型具有高度精确性并且能够用于性能的定量预测（8）、（9）。然而，创建一个使用人工神经网络的性能预测模型需要用到大量的测量数据。此外，参考文献中的例子（8）、（9）都有五个左右的解释变量，并且每个解释变量仅限约三个水平，因此电堆功率精确预测的范围也受到限制。在本次研究中，我们通过实验设计（DoE）方法获取了测量数据，并根据这些数据，采用高斯过程回归模型（10）将11个变量作为输入控制参数，创建了燃料电池电堆功率、压差和出口温度的预测模型。为了增强所建电堆功率预测模型的输出，我们对控制参数变量进行了整体优化，并利用实物燃料电池电堆验证了电堆功率的增强效果。这清楚地表明，通过高斯过程回归模型和少量训练数据创建的电堆功率预测模型，可用来研究增强输出的控制。

1.2.电堆建模概述

表1 输入输出参数的定义

图1是电堆示意图（在专门为本研究创建高斯过程回归模型时，对其进行了评估）。

首先，空间填充技术（11）属于一种实验设计，用于设置实验条件，以便有效地获取训练数据用于机器学习。我们还设计了一款设备，可以全自动执行实验步骤并进行数据的预处理。只需在设备上装载燃料电池电堆即可。该设备可创建实验条件、执行实验、获取并整理实验数据。利用全自动评估系统获得实验数据后，可通过高斯过程回归模型创建燃料电池电堆机器学习统计模型。所建模型的输入和输出如表1所示。易特驰的ETAS ASCMO工具可用于实验设计并创建高斯过程回归模型。

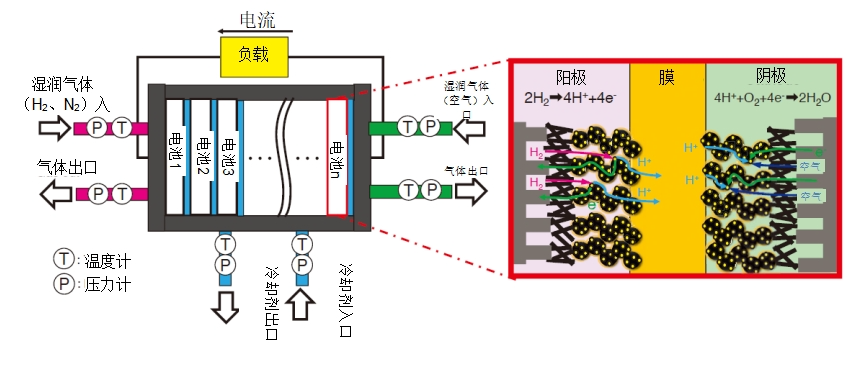
图1 电堆示意图

二

电堆性能评估

2.1. 设定实验条件

通过实验设计设置实验条件时，需要分别设置11个控制参数的上限和下限。设置上限和下限时需要考虑两个方面，即电堆组件的安全以及评估装置控件的上限和下限。举个例子，当电堆内部阳极和阴极之间产生压差时，从电堆保护的角度出发，要对阳极和阴极之间的压差设定一个上限，以保护组件免受压差的影响或防止压差达到或超过某一水平（12）。

2.2. 实验程序

我们为该项实验制造了一个九片电池层状排列的电堆。实验程序的设置如图2所示，基于实验设计在各种测定条件下进行评估。

向阳极和阴极输入氢气（H₂）和氮气（N₂），并调节电堆和加湿器的温度。然后，向阴极输入空气并调节阳极和阴极的背压。如果此时电堆的开路电压保持在1V左右，元件会逐渐发生劣化。因此，我们设定了电流值，稍稍降低了电压。

在电流达到设定值之前，会以1 A/sec的速度发电。该电流会维持30分钟，取最后一分钟的平均值作为目标测量条件下的电堆功率性能。测量结束后，再次向阴极通入N₂，降低电堆电压，在进行温度调节并通入H₂、N₂后对排出的水进行处理。

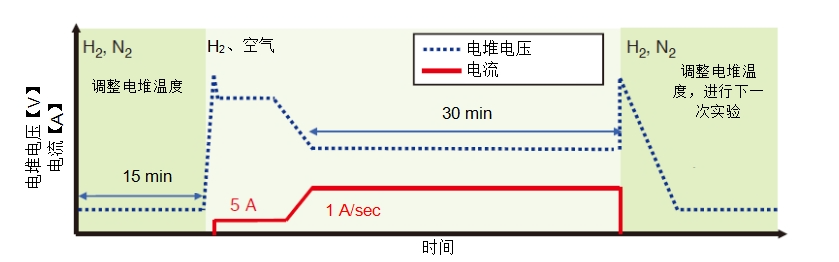
图2 实验方案示意图

2.3.全自动评估系统

我们设计了一个自动评估系统，用于在上述条件和程序下进行实验，并整理数据创建高斯过程回归模型。系统图如图3所示。

全自动评估系统由实验控制系统、实验装置系统和数据分析系统三个主要部分组成。在实验控制系统中，可以基于实验设计（用易特驰ETAS ASCMO软件创建），用11个变量创建装置控制文件，还可以传输转换后可用于实验设备控制的控制配置文件。在实验装置系统中，可基于控制配置文件对上述实验过程进行控制，只有与11个变量相关的控制参数部分是不同的。我们用各种测量仪器测量并用记录器记录了不同条件下的实验数据。数据分析系统会自动整理测量数据，然后按照表1进行标记，将其处理成可供机器学习用的数据。然后使用创建的数据集创建高斯过程回归模型。易特驰的ETAS INCA-FLOW软件可用作管理系统，用于设备全自动操作。

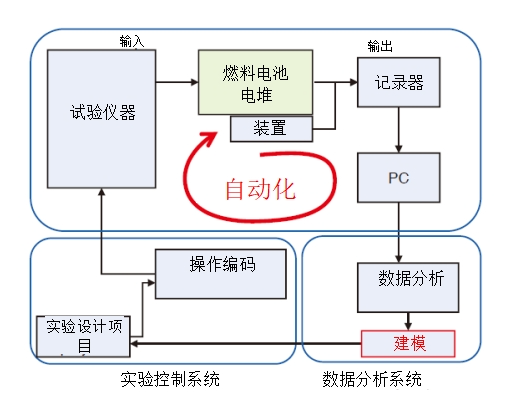
图3 自动化试验流程示意图

2.4. 电堆的高斯过程回归模型

用高斯过程回归模型为电堆建模。高斯过程回归具有非线性的特点，并且由于采用了概率法，模型预测值具有不确定性，但可以计算出不同预测值的概率（10）。

建模中用到的基于高斯过程回归的预测方程如式（1）所示。（13）

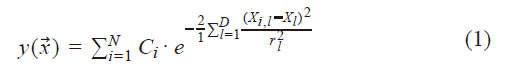
指数函数部分的高斯核函数，采用的是常用的ARD平方指数核。

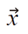是解释变量的输入向量，N是训练数据项的数量，Ci是从超参数导出的第i个训练数据项的系数。D是维数，Xi,l表示训练数据位置，Xl是输入值，rl是长度尺度。其中，Ci和rl是超参数，在ASCMO软件中，这些超参数是通过边际似然优化算法确定的（14）。

在利用空间填充技术设定的实验条件下，我们利用由全自动评估系统获取169个条件组成的数据集创建了高斯过程回归模型。表1是对建模参数的定义（标签）。其中N₂浓度是指输送到阳极入口的气体中N₂所占的比例。阳极和阴极的压差是指电堆入口和出口处的压力差。在为功率建模时，电堆输出是从九片电池的总输出转换为一片电池的等效输出。对于11个已经确定的输入参数，每个输出项都要通过高斯过程回归建模。

使用留一法（LOO）评估所建模型的准确性（15）。可以通过决定系数R²来评估留一法得出的模型精度。如果R²为0.9或以上，则模型可用于定量预测；如果R²为0.6或以上，则模型可用于定性预测（15）。

三

结果与讨论

3.1. 电堆模型评估

根据表1中定义的输入条件为阳极压差、阴极压差、冷却剂出口压力、冷却剂出口温度和电堆功率建模。图4是采用留一法对所建模型进行评估时的结果。我们收集了169项测量数据用于建模。对电堆功率和各种出口参数进行预测时R²>0.9。这表明得到的模型可以用于定量预测稳定状态下的电堆功率、阴极压差、阳极压差以及冷却剂出口温度和压力。

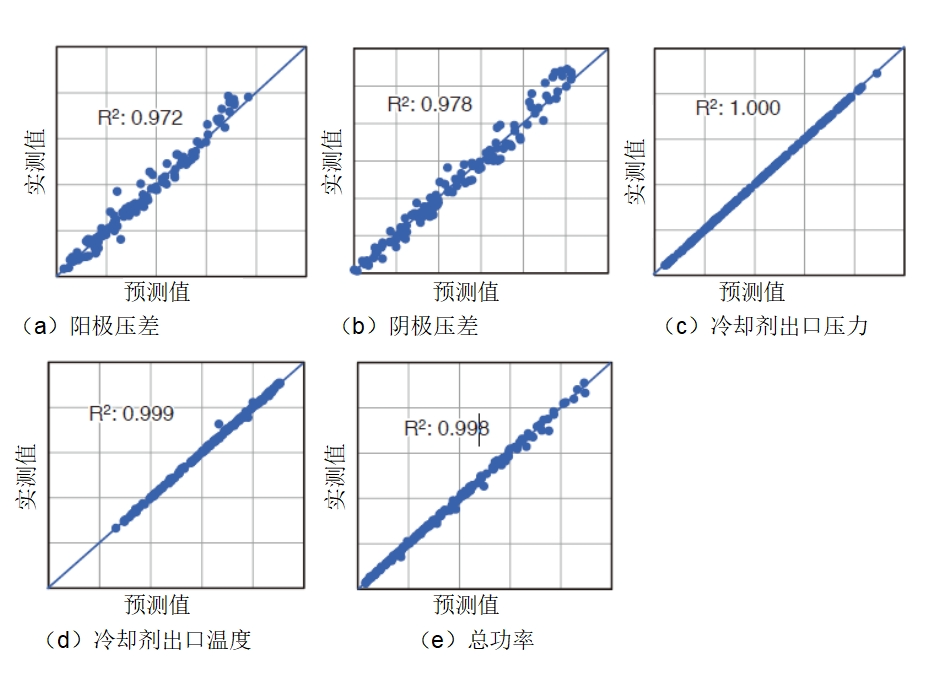
图4 留一法评估结果

基于高斯过程回归模型评估了11个变量对电堆功率的贡献。对功率贡献最大的参数是电流，如果将电流的贡献视为1，则其他参数的相对贡献如图5所示。显然，阳极控制参数的贡献较低，而阴极控制参数的贡献较高。由于燃料电池过电压更多地取决于阴极的氧还原反应，而不是阳极的氢氧化反应（16），显然本研究中功率预测模型所用电堆特性的选择是比较合适的。

图6所示为各标准工况下测得的电堆极化曲线以及将各标准工况下的控制参数输入功率预测模型时预测的平均功率值。利用高斯过程回归模型创建的模型会产生预测值的平均值和标准差σ（10）, （17）。图6给出了±3σ范围内模型预测的平均值。电堆实际测量的极化曲线落在±3σ范围内，表明可以预测各种工作条件下的输出值。

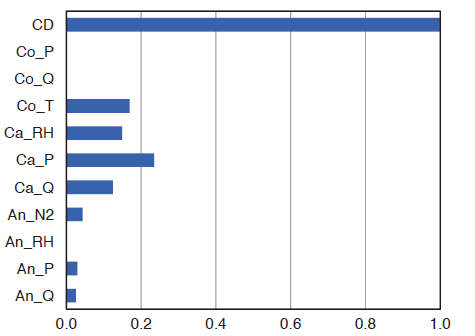
对电堆功率的贡献

图5 输入值与电堆功率的相关性

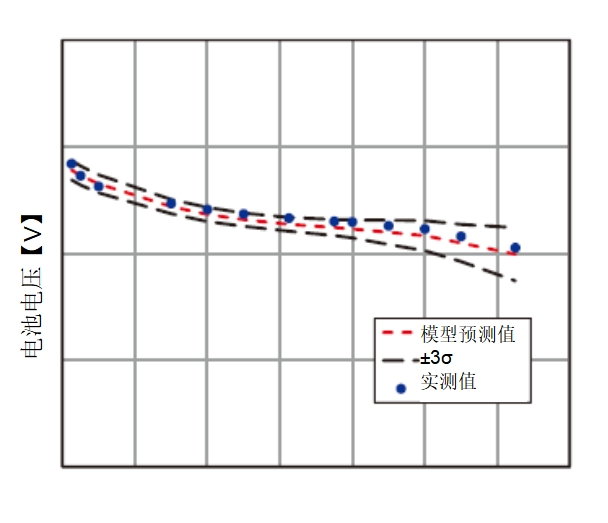
电流密度【A/cm2】

图6 模型预测值与实测数据对比

在图6中，高电流密度下的σ相较于低电流密度下的σ更为分散。这是因为高负载侧的测量数据项的数量约为测量数据项总数的12%，并且学习数据比低负载侧少。

到目前为止，我们采用多路布局进行实验设计，并根据参数化研究结果来预测电堆功率（18）。因此，当多个变量同时变化时测量点的数量会显著增加。那么，想要在多路布局中评估11个变量并创建高精度预测模型，就需要进行数万次实验。本研究采用空间填充技术进行实验设计（实验设计法），利用高斯过程回归建模。这表明，将评估点数减少到数百个时，即使11个相关变量同时发生变化，也可以对各种输出项进行预测。

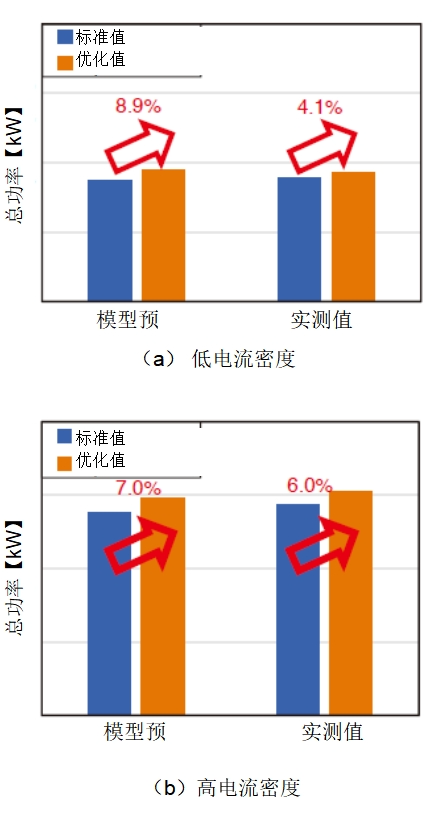
图7 优化参数对电堆功率的影响

3.2. 利用功率预测模型检查控制参数输出增强

关于是否可以用电堆功率预测模型来研究各种控制参数并强化输出，我们已经进行了验证。在验证过程中，我们对控制参数进行了整体优化，以最大化电堆的低电流密度和高电流密度输出。

图7显示了标准条件和优化条件下模型预测输出和测量输出的平均值。所测电堆的规格与建模用电堆的规格相同，但却是不同的电堆。

当标准条件下的控制参数发生改变时，用功率预测模型计算出的平均功率预测值，预计在低电流密度下会增强8.9%，在高电流密度下会增强7.0%。据测算，这一数字分别为4.1%和6.0%。

因此，专门为本研究创建的功率预测模型也可以用来研究电堆功率的增强。

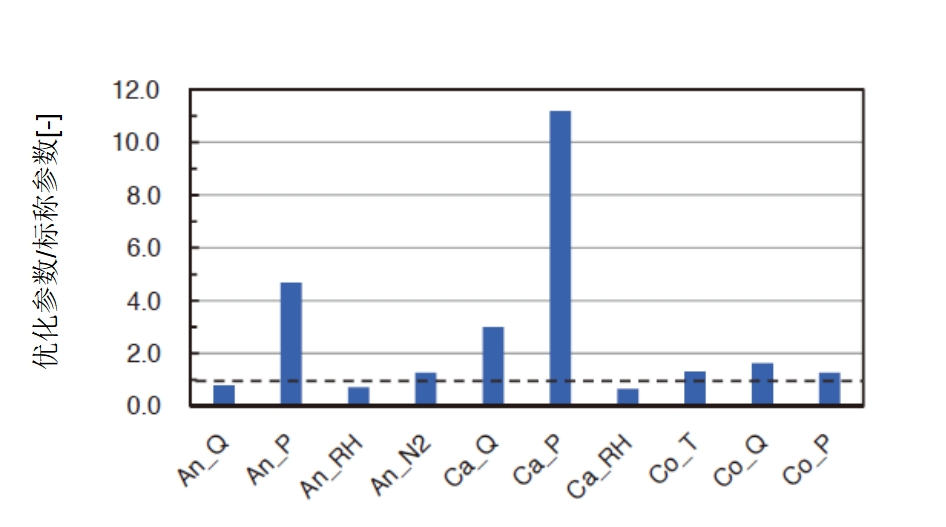
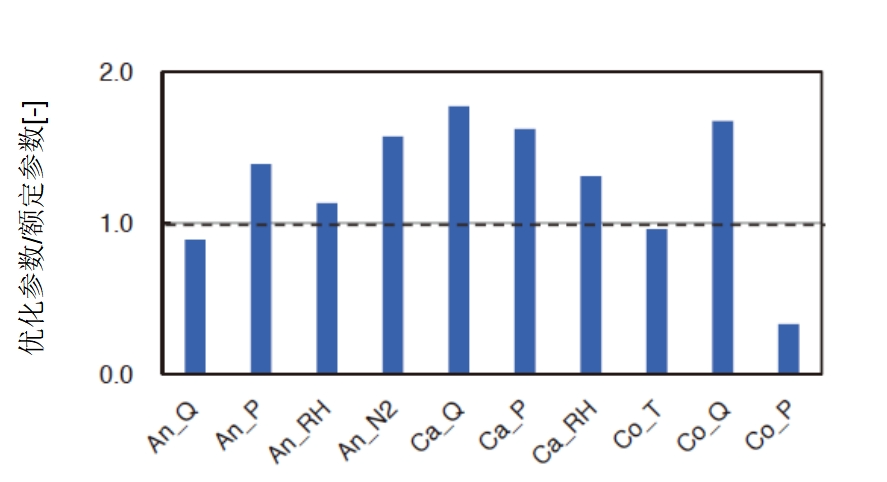
图8列出了总体优化后低电流密度和高电流密度控制参数与标准操作条件下此类参数的比率。条件优化后，可以将阴极压力和阴极流量设置的更高，由于阴极过电压被降低，可以认为功率被增强。另一方面，在阳极，实验条件要求减少流量并提高N₂浓度。可以认为是因为阳极过电压对功率性能几乎没有贡献。图5的结果以及一般燃料电池特性都允许对这些控制参数进行调整（16）。要获得更精确的功率预测模型，可能需要在11个变量构成的多维空间中提高整体数据密度。

（a）低电流密度

（b）高电流密度

图8 优化参数/标称参数之比

本研究中创建的电堆功率预测模型可用于燃料电池系统的持续优化。该系统与实际车辆的电池系统相当，还可以与实际车辆的配件和相关物项匹配。

四

结论

本次研究得出的结果如下：

（1）通过空间填充技术将电堆性能评估点的数量降至最低，根据实验和数据分析用自动化系统获得各种测量数据，利用高斯过程回归为各输出项建模。

（2）利用高斯过程回归模型，优化控制参数，以最大化电堆功率，为研究电堆功率的增强提供了可能。

未来，本文所述模型将用于系统级优化。

审核编辑：刘清