2.1 电路的等效
2.1.1 二端网络
任何一个复杂的电路网络, 如果向外引出两个端钮, 则称为二端网络 ( 一端口网络)。网络内部没有独立源的二端网络,称为无源二端网络;反之,称为有源二端网络。
2.1.2 等效的概念
对于任何两个二端网络,尽管它们的内部结构可能不同,但只要它们端口处的电压-电流关系完全相同,从而它们对联接到该端口上的任一外部电路的作用效果相同,则这两个二端网络互为等效。
这里所谓“完全相同”的含义是指这一相同不应受外部电路的限制,即相同并不只是对某一特定的外部电路而言。
注意:这里的等效,只是指这个二端网络对外部电路等效,在二端网络内部是不等效的。
2.2 简单电阻电路分析
2.2.1 电阻的串联
n个电阻串联时,其等效电阻为 :

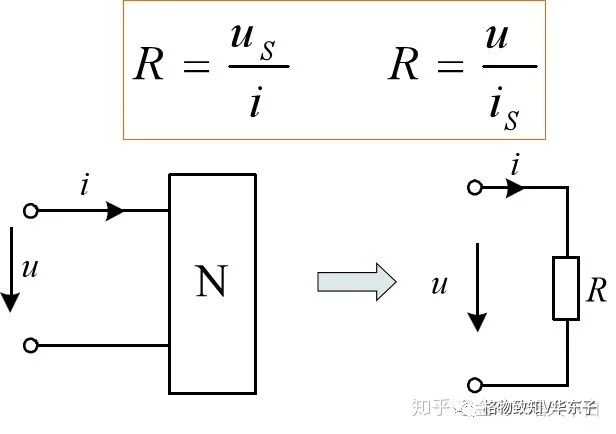
等效电阻:任一无源二端电阻网络,在其二端施加独立电源us(或is),输入电流为i (或u),此网络可等效为一个电阻,即等效电阻为R,其值为:
限流作用:端口电压一定时,串联电阻越多,电流越小,所以串联电阻可以“限流”。
分压作用:串联的各电阻,其两端电压与自身电阻大小成正比,即
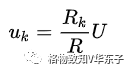
分压公式
2.2.2 电阻的并联

n个电阻并联时,其等效电导为 :

两个电阻的并联公式:
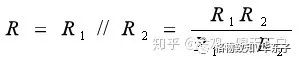
分流公式:并联的各电阻中电流与各电阻大小成反比,即
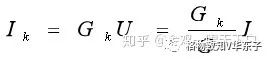
两个电阻并联的分流公式:
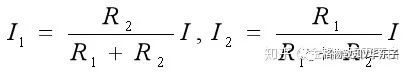
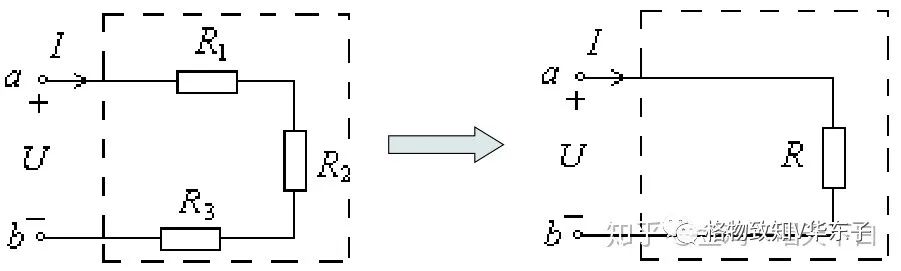
2.2.3 电阻的混联
既有电阻元件串联又有电阻元件并联的电路称为电阻元件的混联。
如下图所示电路:
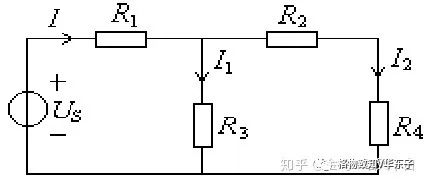
电源右端的网络,等效电阻为:

2.2.4 电阻的三角形连接与星形连接

电阻的三角形连接 电阻的星形连接
等效变换:
等效变换的条件是对应端流入或流出的电流(I1 、I2、I3 )对应相等,对应端间的电压(U1、U2、U3 )也对应相等。

特别的:如果  则有
则有

反过来如果  则有
则有
 2.3 含独立源的简单电路分析
2.3 含独立源的简单电路分析
2.3.1 电压源与电流源之间的等效变换
等效变换的根据:对外电路来说,伏安关系完全相同。
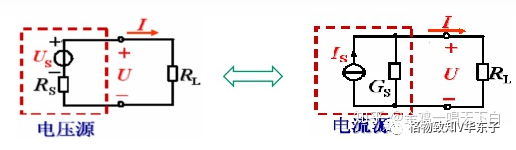
电压源的伏安关系为: 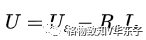
电流源的伏安关系为:
结论就是:等效的条件
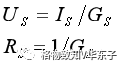
任何一个理想电压源 Us 和一个电阻 Rs串联的电路,都可化为一个电流为 Is 的理想电流源和这个电阻的并联的电路,反之亦然。
两种理想电源不能等效变换;等效变换时,两电源的参考方向要一一对应。
2.3.2 电源串并联电路的分析
1.任何一个网络与一个理想电压源相并联,均可等效为这个理想电压源;
2.任何一个网络与一个理想电流源相串联,均可等效为这个理想电流源;
3.n个理想电压源串联,可以等效为一个电压源Us,且有
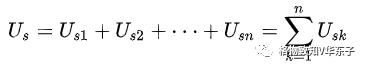
其中,Usk与Us方向一致时其值取正,反之取负。
4.n个理想电流源并联,可以等效为一个电流源Is,且有
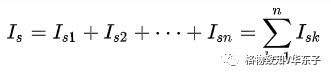
其中,Isk与Is方向一致时其值取正,反之取负。
注意:电压源和电流源的等效关系只对外电路而言,对电源内部则是不等效的。
2.4 含受控源的简单电路的分析
在分析电路时,受控源可当作独立源一样对待。电路基本定律和元件的伏安特性是分析此类电路的依据,也就是仍要用KCL、KVL和VCR。和独立源所不同的是在电路中受控源不能象独立源一样作为独立激励,也就是这类电路不能只有受控源,而没有独立源(局部电路除外)。
2.4.1 受控源的等效变换
受控电压源与电阻串联组合形式可以和受控电流源与电阻并联组合形式之间进行等效变换。
方法:与独立源支路的等效变换基本相同。但变换时一定要注意不要消去控制量,只有先将控制量转化为不会被消去的量以后,才能进行等效变换。
例题:求图示二端网络ab的等效电路。

2.4.2 含受控源的单回路电路和单结点偶电路分析
分析含受控源的简单电路与分析不含受控源的电路方法是相同,只不过会多出控制量这一变量,把控制量用准备求解的变量表示,做为补充方程,方程数仍然是足够的。
2.4.3 含受控源不含独立源的二端网络的等效电路
含受控源不含独立源的二端电阻网络可以等效为一个电阻。
方法是:在端口处施加一个电压或施加电流,然后计算端口的伏安关系,从而求得该二端网络的等效电阻。
例:求图示电路对于端口的等效电阻。
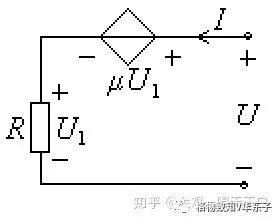
解:在图示电路的端口处施加电压U,然后写出端口电流I与电压U的关系式
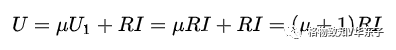
从而求得二端网络的等效电阻为

进一步分析:显然,由于受控源的存在,使端口等效电阻发生变化,等效电阻与参数 μ 相关。
① 二端网络等效为一个电阻,说明该二端网络从外电路吸收电能;
②若  ,则等效电阻小于零,为一负电阻。则这时,该二端网络向外电路提供电能。出现负电阻的原因是由于网络内含受控源,而受控源是可以提供电能的。
,则等效电阻小于零,为一负电阻。则这时,该二端网络向外电路提供电能。出现负电阻的原因是由于网络内含受控源,而受控源是可以提供电能的。
2.5 支路电流法
2.5.1 分析线性电路的一般方法
分析线性电路的一般方法:根据电路元件的伏安特性、欧姆定律、基尔霍夫定律等基本规律,通过列写电路方程来求解电路电压和电流的方法。这种电路方程的列写方法有规律可循,具有一般性(对任何线性电路都适用),故称为一般分析方法。
线性电路方程:通常是一组线性代数方程,非常适合于计算机去处理(解方程)。
复杂线性电路的一般分析法就是根据KCL、KVL及元件的电压与电流关系列方程、解方程。根据列方程时所选变量的不同可分为支路电流法、回路电流法和节点电压法。
一般分析方法的步骤:
① 选取一组合适的电路变量(如支路电流、网孔电流或节点电压等)。
② 根据元件的电压、电流关系特性(VCR)以及KCL、KVL建立一组独立的电路方程。
③ 联立求解方程中的变量。
这里的关键是建立的方程相互间是否独立、以及方程数是否足够。
2.5.2 支路电流法
我们以各支路电流为变量列写方程、解方程的方法称为支路电流法。
一般地说,对具有n个节点,b条支路的电路,只要列出b个独立的电路方程,便可以求解这b个未知量。:
只有(n-1)个节点是独立的,即只能列出(n-1)个KCL 方程;
对于平面电路而言,网孔数为[b -(n-1)]个,恰好为独立回路数,即可列[b -(n-1)]个KVL方程。
因此应用KCL和KVL一共可列出 (n-1)+ [b-(n-1)]=b个独立方程,即可解出b个支路电流。
使用支路电流法的工作步骤:
a.设定每一条支路的电流(  )并标注其参考方向;
)并标注其参考方向;
b. 在n个节点中选定一个参考节点,对其它各独立节点列出(n-1)个 KCL方程;
c. 选取网孔,设定各网孔绕行方向;
d.对各网孔列出[b-(n-1)]个KVL方程 ;
e.联立求解上述的b个独立方程 ,得出并个待求的各支路电流。
可以看到,一个稍微复杂的电路,采用支路电流法列写出的方程组是一个多元方程组,如果不借助于计算机,求解起来非常麻烦。实践中,我们往往也并不需要知道每一条支路的电流,而是部分电流或电压,这就需要我们思考,有没有更简洁的分析电路的方法。
2.6 网孔电流法
什么是网孔电流:沿着网孔边界连续流动的假想电流。要注意,这是一个假想电流,并不是实际存在的,但它和每一条支路的实际电流有关系。
网孔电流法:就是以网孔电流为变量列写方程、求解方程的一种电路分析方法。它仅适用于平面电路。
基本思想:为减少未知量(方程)的个数,假想每个网孔中有一个网孔电流。各支路电流可用网孔电流的线性组合表示,来求得电路的解。
网孔电流在网孔中是闭合的,对每个相关结点均流进一次,流出一次,所以网孔电流在所有节点处都自动满足KCL,因此,只需列出[b -(n-1)]个KVL方程,就可以使得电路得到求解。网孔电流法中的变量—网孔电流个数就是网孔数[b -(n-1)]个。所以网孔电流是一组独立变量。
使用网孔电流法的工作步骤:
① 选定各网孔电流的参考方向,也就是列方程式时这个网孔的绕行方向。
② 列写 [m=b -(n-1)]个网孔的KVL方程。

其中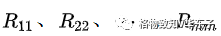 称为网孔1-m的自电阻,为该网孔中所有电阻之和;
称为网孔1-m的自电阻,为该网孔中所有电阻之和;
其余电阻为各个网孔之间的互电阻:计算方法是两个相邻网孔公共支路中所有电阻之和,不相邻则互电阻为零);当通过该互电阻的两个网孔电流的参考方向一致时,互电阻取正号;参考方向相反时,取负号。
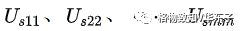 为网孔1-m中所有电源两端电压的代数和。注意此处,在求这个代数和时,如果某个电源电压方向与绕行方向相同取负号,否则取正号。
为网孔1-m中所有电源两端电压的代数和。注意此处,在求这个代数和时,如果某个电源电压方向与绕行方向相同取负号,否则取正号。
③ 联立取求解网孔电流方程,得到网孔电流。
④ 指定待求支路电流的参考方向。此支路电流为与其相关的网孔电流的代数和,列写方程,从而求出待求支路电流。
下面单独说一下,含理想电流源支路时的求解方法:
如能使这个电流源中只有一个网孔电流流过,则该网孔电流就等于此电流源的电流,而不必对这个网孔列网孔方程了;
如不能使电流源中只有一个网孔电流流过。则需要把电流源的电压也作为变量列入网孔方程,并将电流源电流与有关网孔电流的关系作为补充方程,方程数仍然足够,就可以一并求解。
2.7 节点电压法
节点电压:确定某个节点作为参考节点(理论上那个节点都可以),则其余任意独立节点到该参考节点的电压,就成为该节点的节点电压。
要注意,这是一个假想电压,并不是实际存在的,但它和每一条支路的实际电压有关系。
节点电压法:就是以节点电压为变量列写方程、求解方程的一种电路分析方法。适用于节点较少的电路。
基本思想:选节点电压为未知量,则KVL自动满足,无需列写KVL 方程。各支路电流、电压可视为节点电压的线性组合,求出节点电压后,便可方便地得到各支路电压、电流。
节点电压在所有网孔都自动满足KVL,因此,只需列出(n-1)个KCL方程,就可以使得电路得到求解。节点电压法中的变量—节点电压个数就是其余独立节点数(n-1)个。所以节点电压是一组独立变量。
使用节点电压法的工作步骤:
① 选定各节点电压的参考方向,也就是列方程式时这个节点的电压方向。
② 列写(n-1)个节点的KCL方程。

其中
 称为节点1-(n-1)的自电导,为与该节点相连的各支路的所有电导之和;
称为节点1-(n-1)的自电导,为与该节点相连的各支路的所有电导之和;
其余电导为各个节点的互电导:计算方法是两个相邻节点公共支路中所有电导之和的负值,不相邻则互电导为零)。
 为节点1-(n-1)中所有流入该节点的电源电流的代数和。注意此处,在求这个代数和时,流入为正,流出为负。
为节点1-(n-1)中所有流入该节点的电源电流的代数和。注意此处,在求这个代数和时,流入为正,流出为负。
若支路为电压源与电阻串联,则电流为电压源与电阻之比,当电压源正极性端连接该结点时取正,反之取负。
③ 联立取求解节点电压方程,得到节点电压。
④ 指定待求支路电流的参考方向,根据欧姆定律就可求出该支路的电流。
下面单独说一下,含理想电压源支路时的求解方法:
尽可能取电压源支路的负极性端作为参考结点。则该支路的另一端电压为电压源电压,因而不必再对此节点列写节点电压方程;
如不能使电流源中只有一个网孔电流流过。则需要把电流源的电压也作为变量列入网孔方程,并将电流源电流与有关网孔电流的关系作为补充方程,方程数仍然是足够的,就可以一并求解了。
弥尔曼定理:
单结点偶电路:有两个结点多个支路的电路。所以它只有一个独立结点,只有一个变量,只需要列写一个方程。
独立节点的电压U1的计算公式:

-
电阻电路
+关注
关注
0文章
51浏览量
11618 -
等效变换
+关注
关注
0文章
32浏览量
10680 -
等效电阻
+关注
关注
7文章
60浏览量
11430 -
直流电路
+关注
关注
3文章
120浏览量
13713 -
支路电流法
+关注
关注
0文章
17浏览量
6767
发布评论请先 登录
相关推荐
变压器直流电阻测试仪一般选多大的电流的
直流电路的过流保护设计方法
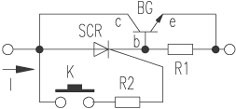




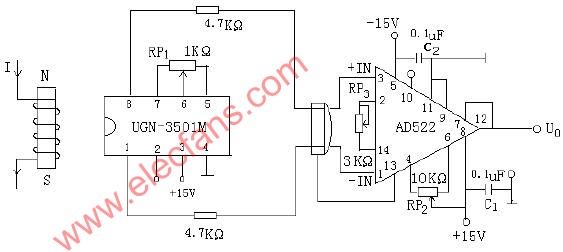
 直流电路的一般分析方法
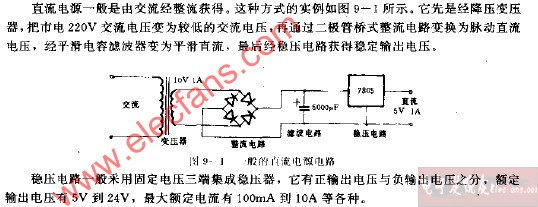
直流电路的一般分析方法











评论