电感是什么？电感三个法则

一、电感是什么

对于线间耦合、电源分配网络以及电磁干扰问题，电感就是信号沿均匀传输线传播过程中遇到的突变。

导线绕成的线圈或螺丝管的电感，其中有磁力线通过。或者说，电感是对表面磁场强度的数值积分。

   

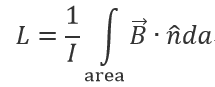
二、电感三个法则

法则之一：电流周围会形成闭合磁力线圈

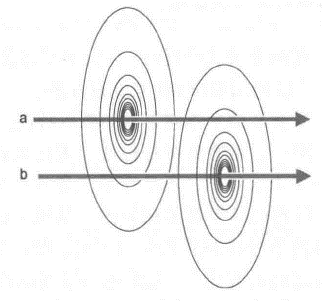
磁力线是一个新的基本实体，它环绕在所有电流的周围。

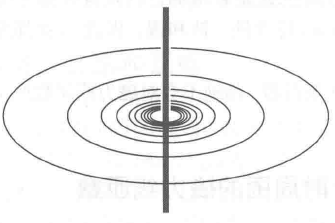
电流周围的一些环形磁力线圈。

从上到下，导线周围都存在磁力线圈。

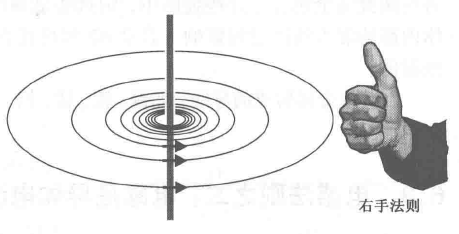
磁力线圈的环绕方向遵循右手法则

电流周围的磁力线匝数，单位为韦伯（Weber，简写Wb）。

导线电流周围的磁力线匝数受影响的因素：

1.导体中电流的大小。

2.导线的长度。

3.导线的横截面。

4.附近其他电流的存在也会对第一个电流周围的磁力线匝数产生影响。所谓的特殊电流是返回电流。

注：磁场根本不会与电介质材料相互影响。

5.影响电流周围磁力线匝数的可能因素还有导线的金属。（铁、钴、镍）

法则之二：电感是导体电流1A 时周围的磁力线匝数

电感是当导体通过单位安培电流时其周围磁力线匝数的度量：

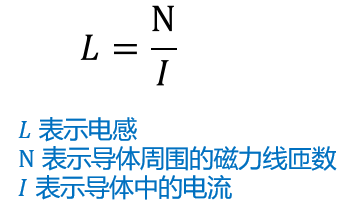
电感与导线中的电流无关，电感值不涉及电流周围的磁场密度及其聚集度，也不涉及存储在磁场中的能量值。仅仅涉及当每安培电感产生磁力线圈时，各种导体几何结构的不同效率。

当计算一条导线周围的磁力线圈时，需要有一种方式表明磁力线圈的源头。我们把一条导线自身电流产生的磁力线圈称为自磁力线圈（self-filed line ring），把由邻近电流产生的磁力线圈称为互磁力线圈（mutual-filed line ring）。

为了分清磁力线圈的源头，引入了自感和互感。

自感：导线中流过单位安培电流时，所产生的环绕在导线自身周围的磁力线匝数。通常我们所说的电感实际上就是导线的自感。

互感：一条导线中流过单位安培电流时，所产生的环绕在另一条导线周围的磁力线匝数。

互感有两个不同寻常的特性：

1.互感具有对称性。

2.两条导线之间的互感小于二者中任一个的自感。

如果电流方向相同，这时第一条导线周围的磁力线匝总数等于其自磁力线圈匝数加上互磁力线匝数。

如果电流方向相反，这时第一条导线周围的自磁力线圈与互磁力线圈的方向也相反，这时应从自磁力线匝数中减去互磁力线匝数，从而使第一条导线周围的磁力线匝总数相应地减少。

法则之三：周围磁力线匝数改变时导体两端产生感应电压

重要的特殊性质：无论什么原因，只要一段导线周围的磁力线匝总数发生变化，导线两端就会产生一个感应电压。

感应电压正是电感在信号完整性中意义重大的根本原因。如果电流变化时没有产生感应电压，信号就不会受到电感的影响。这个由电流变化产生的感应电压引起了传输线效应、突变、串扰、开关噪声、轨道塌陷、地弹和大多数电磁干扰源。

三、局部电感

实际的电流是在完整的回路中流动。局部电感的概念是一个纯粹的数学构造，它是不可测量的，因为实际中并不存在孤立的局部电流。

局部电感分为局部自感和局部互感。

封装中的引线、连接器引脚和表面走线的电感时，实际上指的是该互连元件的局部自感。

对于直圆杆导线，局部自感近似式：

从上式中，当导线长度增加时，局部自感会增大。但是局部自感增大比线性增长得快。如果导线长度加倍，则局部自感的增长将远大于两倍。这是因为当导线长度增加时，环绕在新增导线线段周围的磁力线圈，除了源于这段电流，还包括源于其他线段电流的一些互磁力线圈。

当两个导线段间距远大于导线长度时，两段导线间的局部互感小于任一段导线局部自感的10%, 这时互感通常可以忽略不计。

如果互连中两段之间的间距大于两段的长度，它们之间的耦合就不再重要。例如，两个长为20mil的过孔，当它们的中心距大于20mil时，这两个过孔之间就几乎没有耦合。

局部电感实际上就是电感概念的基础，其他所有类似的电感都是用局部电感加以描述。

四、有效电感、总电感或净电感及地弹

回路中某一段的有效电感、总电感或净电感是指回路中的电流为单位安培时，环绕在该段周围的磁力线总匝数，其中包括整个回路中任何电流段产生的磁力线。

有两个支路的电流回路：初始电流和返回电流

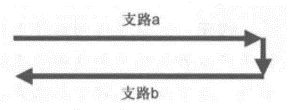
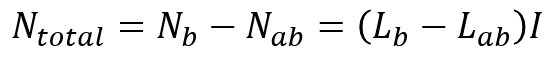
当相邻电流的方向相反时，如回路的两条支路的一条是另一条的返回电流路径时，有效电感决定回路电流变化时支路两端感应电压的大小。如果第二条支路是返回路径，则称为在该返回路径上产生的电压为地弹。

最小化返回路径上的电压降（即地弹电压）有两种方法：

第一种方法，尽可能减小回路电流的变化速率。

第二种方法，尽可能减小L_total。减小返回路径总电感的要点有两方面：减小支路的自感，增大两支路之间的局部互感。

减小返回支路的局部自感就是使返回路径尽可能短、尽可能宽（也就是使用平面）；增大返回路径和初始路径之间的互感就是使第一条支路与其返回路径尽可能地靠近。

另一种情况，两条导线里流过的都是电源电流。这种情况在许多集成电路封装中十分常见，因为常常使用多条引脚传输电源电流和地电流。

电流方向相同，互磁力线圈和自磁力线圈方向相同，二者是相叠加的，所以其中一根电源导线的净电感为：L_total=L_b+L_ab。，由于临近引线产生的磁力线方向相同，所以还是要必须尽可能地减小引线之间的局部互感。换言之，导线的间距要尽可能大。

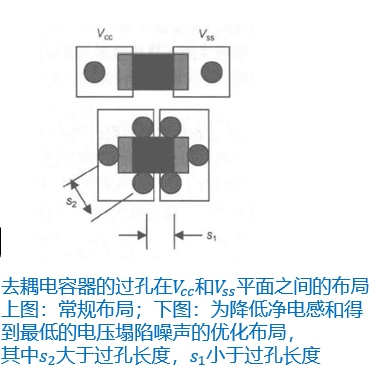
过孔：电流方向相同的过孔间的中心距应至少等于过孔的长度。从焊盘到下面的平面之间有多个过孔并联，则等效电就会减小，并与过孔数呈相反的关系，即并联的过孔数目越多，等效电感就越小。在图中， S2应至少约等于到平面的距离20mil。

电流方向相反的过孔间的中心距要小于过孔的长度。S1<20mil，则每个过孔的净电感将降低，从而焊盘到平面之间的等效电感和轨道坍陷电压也会减小。

   

五、回路自感和回路互感

在实际中，电流总是在完整的回路中流动，我们把该完整电流的回路的总电感称为回路电感。回路电感事实上就是整个电流向路的自感，或者回路自感。

3种重要特殊几何结构：环形线圈、长的平行双圆杆和两个宽平板。它们的回路电感有很好的近似公式。

对于环形线圈，其回路电感为：

经验法则：将拇指和食指围成一个圆，用30 AWG导线构成同等大小的回路，其回路电感大约为85nH（30 AWG线规的导线大约10 mil 粗，将其弯成一个直径为1 in 的圆）。直径为1in 的线圈的单位长度的回路电感约为25nH/in。

对于相邻的双圆杆，若其中一条为另一条的返回电流路径，则回路电感为：

任何阻抗可控互连的单位长度回路电感都是恒定的。

六、电源分配网络和回路电感

电源分配网络的用途是在每个芯片的电源焊盘和地焊盘之间提供恒定的电压。根据器件工艺的不同，该电压范围一般为0.8~5V ，大多数总体方案分配的噪声波动预算一般不超过5%。

在稳压器和芯片之间有许多互连，如过孔、平面、封装引线和键合线等。如果进入芯片的电流发生突变（如程序的执行引起某些门的同时切换、时钟边沿处的大量的门将同时切换），则当变化的电流流过电源分配网络的互连阻抗时就会引起电压降，称为轨道下沉或轨道塌陷。

多大的去耦电容？

通过设想在时间段At 内，去耦电容必须提供的电荷量来大数估算出来。

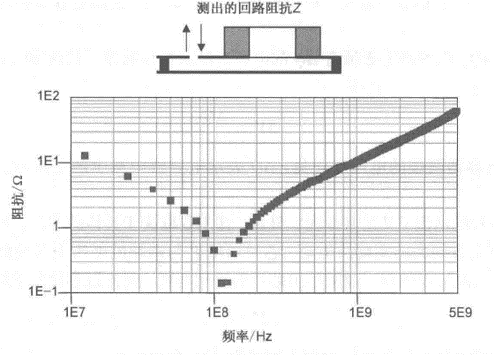
实际电容器的两端和芯片焊盘相连的那段线条会有相应的回路电感。该回路电感与理想电容元件相串联，导致实际电容器的阻抗随频率的升高而增大。

低频时，正如理想电容器，阻抗随频率的增大而减小。但是，随着频率升高，从某一点起，串联的回路电感开始在阻抗中起主导作用。该点的频率称为自谐振频率。

当频率大于自谐振频率时，电容器的阻抗与电容量完全无关，只与相应的回路电感有关。所以，频率较高时，如果想减小去耦电容器的阻抗，就要减小相关的回路电感，而不是靠增大电容量。

减小去耦电容器的回路电感的方法：

1.使电源平面和地平面靠近电路板表面层，以缩短过孔；2.使用尺寸较小的电容器；3.从电容器焊盘到过孔之间的连线要尽量短；4.将多个电容器并联使用。

   

七、每方块回路电感

由两个平面构成的电流路径的回路电感，取决于每个平面路径的局部自感和它们之间的局部互感。

对于宽导体，宽度w远大于它们的间距h，即w》h，两平面之间的回路电感就可以很好地近似：

   

八、平面对与过孔的回路电感

平面对之间的电流并不是从一边直接流向另一边的。从分立去耦电容器到芯片封装引脚，它们与平面的连接更像是点接触。实际中电流并不是均匀流动的，如果电流由于点接触而受到限制，那么回路电感将会变大。

第一种情况，上平面的一边作为电流的源端，与之相邻的下平面的那一边作为电流的漏端，两平面另外较远的边短接在一起。

第二种情况，在两平面的一端上下各有一个小接触过孔，分别作为电流的源端和漏端。在另一端，也有一对相似的接触过孔将两平面短接在一起。其中每对接触孔的直径为10mil，中心距为25mil，这与实际电路板上连接平面的接触过孔对是一样的。

经验法则：接触孔直径为 10mil 时，平面间的回路电感约是没有过孔时两相邻平面的单位面积回路电感的4 倍。

九、有出砂孔区域的平面对的回路电感

经常能看到过孔阵列，如球栅阵列封装下，连接器处和电路板上的高密度区域。通常，过孔的电源平面和地平面上会有许多出砂孔。

为了减小出砂孔的影响，就要把出砂孔做得尽量小。当然，无论有无出砂孔，缩小平面间距都可以减小回路电感。

   

十、回路互感

两个相互独立的电流回路，那么它们之间就会产生互感。回路互感就是第一条回路中有 1 A 电流通过时，它所产生的环绕在第一条回路周围的磁力线匝数。

当第一条回路中的电流发生变化时，环绕在第二条回路周围的磁力线匝数就会改变而且还会产生噪声值为：

只有当动态回路中的电流变化时，在静态回路中才会产生噪声。而这种情况仅在开关跳变时才发生。这就是该类噪声经常称为开关噪声、同时开关噪声（SSN）或∆I噪声原因。

十一、多个电感器的等效电感

两个分立的互连元件，它们有两种连接方式：串联和并联。

对于两个局部电感的串联，其等效的局部自感为：

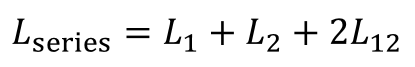
当两个元件并联连接时，其等效的局部自感为：

   

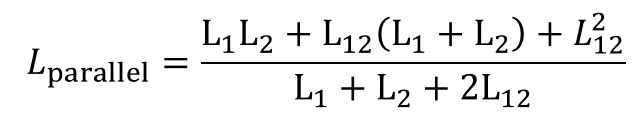
十二、电感的分类

电感的分类与流过单位安培电流时导体周围的磁力线匝数有直接的关系。电感的重要性在于，当电流变化时导体上会产生感应电压。

为了清楚起见，对于自感或互感，需要指明其电流的源头，然后说明是指部分电路的局部电感还是整个电路的回路电感。

如果考虑的是电路中某一段的电压噪声，那么由于该电压噪声取决于所有磁力线匝数及其变化，所以需要弄清楚电路上这一段的总电感。

最后，如果是多个电感器的组合，如封装中多条平行引线并联或多个孔并联，就要用到等效电感。

分类：1.电感；2.自感；3.互感；4.回路电感；5.回路自感；6.回路互感；7.局部互感；8.局部自感；9.局部互感；10.有效电感、净电感或总电感；11.等效电感。

十三、电流分布及集肤深度

直流时，实心铜棒中的电流是均匀分布的。前面计算磁力线匝数时，重点关注了导线外部的磁力线。事实上，在导线内部也有一些磁力线，它们是自感的一部分。

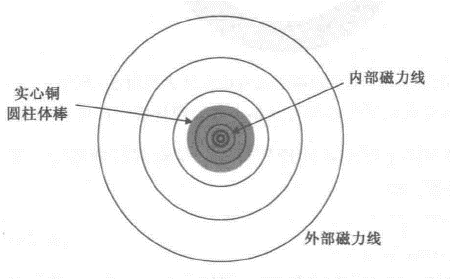
交流时，电流是正弦波，任何频率分量都是沿着最低阻抗路径传播的。电感最大的电流路径，其阻抗也是最大的，随着频率的升高，高电感路径的阻抗会变得更大。频率越高，电流越倾向于选择电感较低的路径，即趋向于圆柱杆外表面的路径。

圆柱体的几何结构中，可以把电流层近似成固定厚度δ均匀分布，并称该等效厚度为集肤深度，它取决于频率、金属的电导率和磁导率。

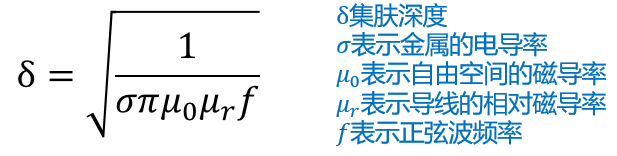
铜的电导率为5.6 x 10^7 S/m，相对磁导率为1，它的集肤深度近似为：

由于趋肤效应的影响而使电流流过的横截面很薄，则互连线的电阻就会增大。

直流时，导线的自感由外部自感和内部自感两部分组成。当导线中的电流重新分布时，外部自感不变，但随着越来越多的电流向导线表面移动，内部自感也越来越小，当频率远高千趋肤深度和几何厚薄相当的这个频率时，导线内部的电流会非常小，而内部自感此时几乎为零。

十四、高磁导率材料

导体的磁导率是影响集肤深度的重要参数。磁导率是导体与磁力线圈之间的相互作用，大多数金属的磁导率为1，所以它们对磁力线圈没有影响。

只有3种金属的磁导率大于1，它们是铁磁体金属：铁、钴和镍。大多数含有这些金属合金的磁导率都远大于1 。

十五、涡流

如果两个导体中有一个导体的电流改变，那么另外一个导体的两端会产生感应电压，此感应电压会形成电流。换言之，当其中一个导体的电流变化时，第二个导体中会产生感应电流，我们称这种电流为涡流。

当导线中有电流时，一些磁力线就会穿过导电平面，导线与平面之间就会存在互感。当导线中的电流变化时，穿过平面的磁力线也会发生变化，并在平面上产生感应电压，而此电压又激起涡流，这些涡流反过来又会产生自己的磁力线。

十六、总结

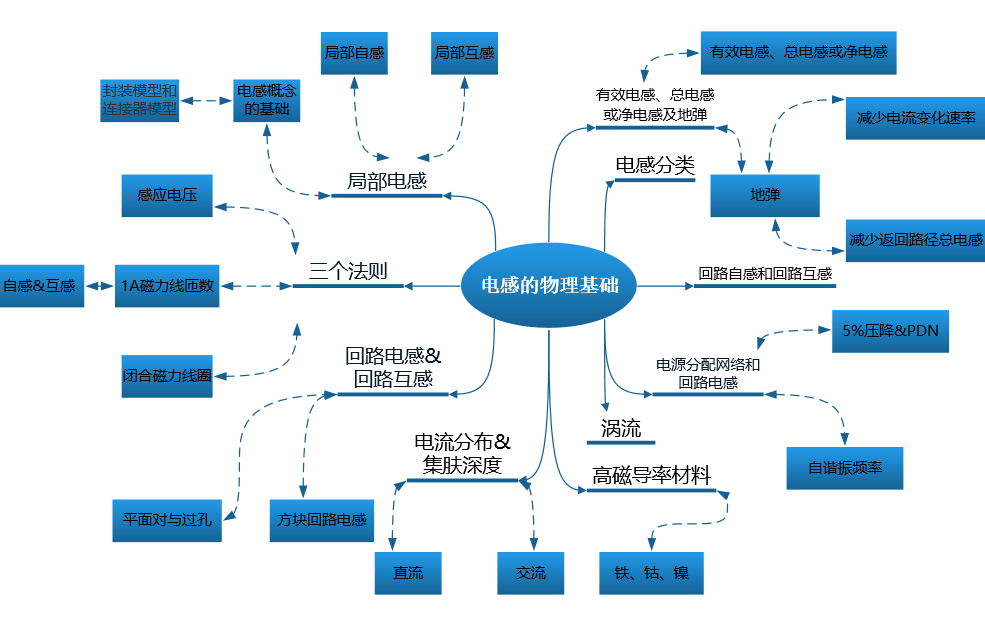  电阻的物理基础总结

前言

•所有互连和无源元件的电气描述都基于3种理想的集总电路元件（电阻器、电容器和电感器）和一个分布元件（传输线）。

•所有互连的电气特性都能用麦克斯韦方程组加以描述，这4个方程描述电场和磁场是如何与边界条件（即一些几何结构中的导体和介质）相互作用的。

•麦克斯韦方程组的四个方程：描述静电的高斯电场定律、描述静磁的高斯磁场定律、描述磁生电的法拉第定律和描述电生磁的安培-麦克斯韦定律的积分形式。

 

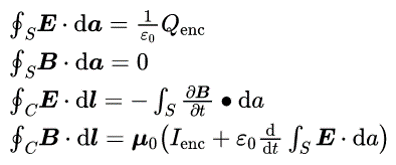
一、将物理设计转化为电气性能

•考察互连电气性能的基本就是它的等效电路模型。

•所有模型由两部分组成：电路拓扑结构和各个电路元件的参数值。

•任何互连建模的基础就是使用3种理想集总电路元件（电阻器、电容器和电感器）和分布元件（理想传输线电路元件）的一些组合。

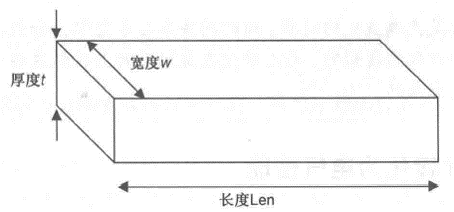
•建模就是将物理设计中线的长、宽、厚和材料特性转化为R，L和C的电气描述形式。

•建立互连电路模型的拓扑结构，下一步就是提取参数值，这个过程有时称为寄生参数提取，或寄生提取。

以微带线互连这一特殊情况，给出物理和电气两种不同的视图：

 

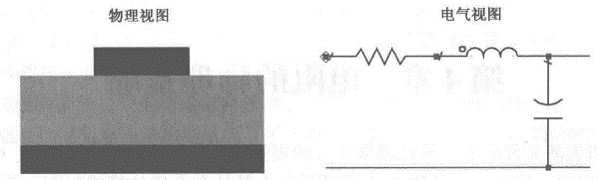
二、 互连电阻的最佳近似式

•提取互连的电阻时，实际上无形中已经假定要以理想电阻器作为互连的模型。实际铜线两端之间的阻抗看起来非常像理想电阻器，它在时域和频域中都是恒定的。

•对于互连电阻，给出一个良好的解析近似式，但是这种近似只用于均匀横截面的导线。

•导线横截面恒定，电阻值可由下式近似式：

•经验法则：直径为 1 mil且长为80 mil的键合线的电阻值约为0.1 Ω

•等效的理想电阻器的参数值与结构的几何尺寸和材料特性（也就是体电阻率）有关。如果改变导线的形状，等效的阻值也会改变。

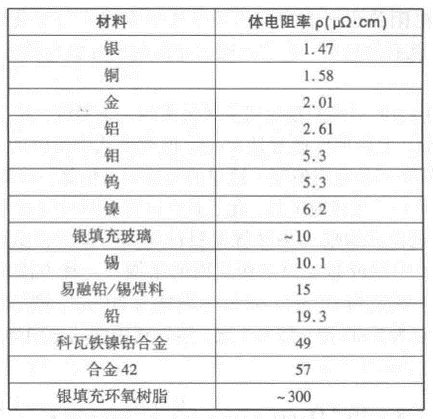
三、 体电阻率

•体电阻率是所有导线都具有的一个基本材料特性。它不是由材料构成的物体的结构特性，它与物理的尺寸无关。边长1mil 的铜与边长1 in 的铜有相同的体电阻率。

•不要把体电阻率与一段互连具有的电阻值相混淆。

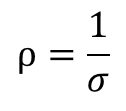
•铜的体电阻率为1.8~4.5 μΩ·cm，取决于它是否电镀、非电方式淀积、喷涂、冲压或退火等。

•材料越疏松，它的体电阻率就越高。

 

四、单位长度电阻

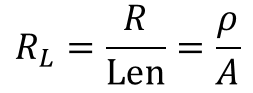
•键合线的单位长度电阻约为 1 Ω/in

•导线的直径采用美国线规（AWG）设定的标准数据分类。

•直径越大，阻抗越低，损耗越小

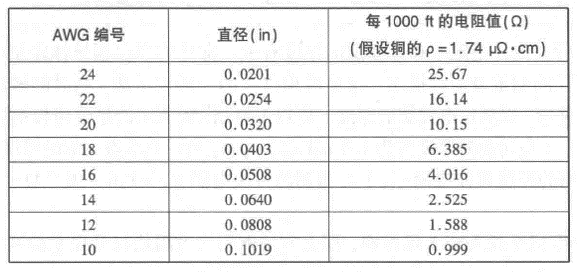
五、方块电阻

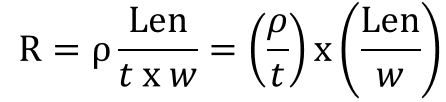
•第一项（ρ∕t）,对于该层上厚度为t的所有线条而言是个常数。在同一层上的所有线条都有相同的体电阻率和相同的厚度，所以这一项称为同一层的方块电阻值，并用Rsq表示：

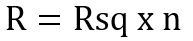
•第二项（Len/w）是具体线条长与宽的比值。这是线条所能划分的方块数，用 n 来表示，是个无量纲的数。

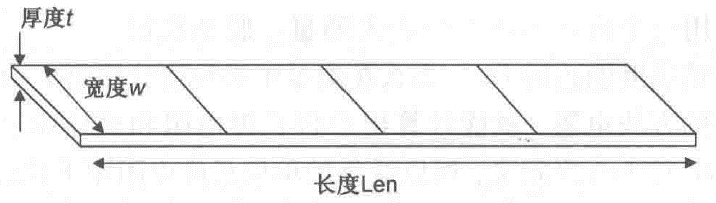
•无论正方形边长是10mil还是10 in ，其相对两端之间的电阻恒定不变。如果长度加倍，则可能以为电阻值会加倍，然而宽度加倍，所以电阻值减半。这两种作用相互抵消，使得正方形的尺寸改变时，净电阻仍保持不变。

•1盎司铜表示电路板铜层每平方英尺的铜的重量，1oz =28.3495 g。

•1盎司铜的厚度约为1.4 mil或35 um •经验法则：0.5 盎司铜的方块电阻是 1 m Ω / s q 。5 mil 宽、5 in 长的线条可以截取成1000 个串联的方块并且阻值是1Ω。

•线越宽，单位长度电阻越小。许多背板设计中常见的5 mil宽的线条，0.5盎司铜导线的单位长度电阻是0.2 Ω∕in （1.0 盎司铜导线的单位长度电阻是0.1 Ω∕in）（注：键合线的单位长度电阻约为 1 Ω/in相区别）。

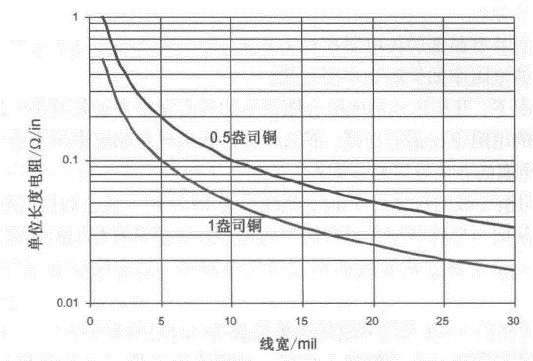
•目前为止，阻值计算都是在直流时或至少是低频情况下的电阻。

•由于趋肤效应的影响，线条的阻值将随着频率的升高而加大。虽然铜的体电阻率不变，但导线上的电流分布却发生了改变。高频信号分量在贴近表面的很薄的层上传播，进而使有效面积减小。对于1盎司的铜导线，电阻值从20MHz的频率处开始增加，并且大致随着频率的平方根增加，这些又都与电感有关。

交变电流通过导线时，电流在导线横截面上的分布是不均匀的，导体表面的电流密度大于中心的密度，且交变电流的频率越高，这种趋势越明显，该现象称为趋肤效应（Skin effect）。

趋肤效应热成像

总结：

1.电阻的相关概念（互连电阻）

2.体电阻率部分建议深入了解一下，后期相关产品的cable部分，链路损耗部分可能会考虑其因素。

3.拓展知识：1盎司铜的相关知识&趋肤效应。

审核编辑：汤梓红