使用傅里叶变换进行图像边缘检测

今天我们介绍通过傅里叶变换求得图像的边缘

什么是傅立叶变换？

简单来说，傅里叶变换是将输入的信号分解成指定样式的构造块。例如，首先通过叠加具有不同频率的两个或更多个正弦函数而生成信号f（x），之后，仅查看f（x）的图像缺无法了解使用哪种或多少原始函数来生成f（x）。

这就是傅立叶变换最神奇的地方。将f（x）函数通过一个傅立叶变换器，我们就可以得到一个新的函数F（x）。F（x）的是最初生成f（x）函数的频率图。因此，通过查看F（x）我们就可以得到用于生成f（x）函数的原始频率。实际上，傅立叶变换可以揭示信号的重要特征，即其频率分量。

例如下图，该图中有f（x）函数合成时的两个不同频率的原函数和对应的傅里叶变换结果F（x）。

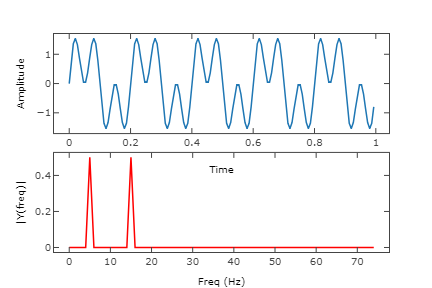
生成该图片的代码如下：

Fs = 150.0; ＃采样率
Ts = 1.0 / Fs; ＃采样间隔
t = np.arange（0,1，Ts）＃时间向量
ff1 = 5; ＃信号频率1 
ff2 = 10; ＃信号2的频率
y = np.sin（2 * np.pi * ff1 * t）+ np.sin（3 * np.pi * ff2 * t）

从图中可以看出，由于原始函数是由两个不同频率的输入函数组成的，因此经过傅立叶变换后的相应频率图显示了两个不同频率的尖峰。

这是对傅立叶变换的比较简单的解释。它是一个非常复杂但非常有用的功能，在数学，物理和计算机视觉中得到了广泛的应用。

图像处理中的傅立叶变换

现在我们知道了傅里叶变换对信号处理的作用。它将输入信号从时域转换到频域。

但是它在图像处理中有什么用？它将输入图像从空间域转换为频域。换句话说，如果要在进行傅立叶变换后绘制图像，我们将看到的只是高频和低频的频谱图。高频偏向图像中心，而低频偏向周围。具体形式如下图所示。

上面对图像进行傅里叶变换的结果可以通过如下代码实现：

import numpy as np 
import cv2 from matplotlib 
import pyplot as plt 
img = cv2.imread('scenery.jpg', 0) 
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft) magnitude_spectrum = 20 *    np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1])) 
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray') 
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 2), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('After FFT'), plt.xticks([]), plt.yticks([])

现在我们可以对图像进行FFT（快速傅里叶变换）变换了，并且可以使用转换后的结果进行多种操作：

边缘检测—使用高通滤波器或带通滤波器

降噪—使用低通滤波器

图像模糊-使用低通滤镜

特征提取（在某些情况下）-过滤器和其他一些openCV工具的混合搭配

HPF滤波器

如前所述，在经过FFT变换的图像中，在中心处发现低频，而在周围散布了高频，我们可以创建一个掩码数组，该掩码数组的中心是一个圆，其余全部为零。当将此掩码数组作用于原始图像时，所得图像将仅具有低频。由于高频对应于空间域中的边缘，这样就可以实现图像中的边缘检测。这个掩码数组就时HPF滤波器。

我们可以通过如下代码生成HPF滤波器

mask = np.ones((rows, cols, 2), np.uint8) 
r = 80 center = [crow, ccol] 
x, y = np.ogrid[:rows, :cols] 
mask_area = (x - center[0]) ** 2 + (y - center[1]) ** 2 <= r*r

尽管可以选择使用多种类型的过滤器，但是主要使用三种类型的过滤器：

高通滤波器（HPF）

低通滤波器（LPF）

带通滤波器（BPF）

使用openCV和NumPy的高通滤波器进行边缘检测

在计算机视觉领域中，检测图像边缘非常有用。一旦我们可以提取图像中的边缘，就可以将该知识用于特征提取或模式检测。

图像中的边缘通常由高频组成。因此，在对图像进行FFT（快速傅立叶变换）后，我们需要对FFT变换后的图像应用高通滤波器。该滤波器会阻止所有低频，仅允许高频通过。最后，我们对经过了滤波器的图像进行逆FFT，就会得到原始图像中一些明显的边缘特征。

接下来，我们使用汽车的图像进行此实验，这个过程的代码如下所示：

rows, cols = img.shape 
crow, ccol = int(rows / 2), int(cols / 2) # center 
# Circular HPF mask, center circle is 0, remaining all ones 
mask = np.ones((rows, cols, 2), np.uint8) 
r = 80 center = [crow, ccol] 
x, y = np.ogrid[:rows, :cols] 
mask_area = (x - center[0]) ** 2 + (y - center[1]) ** 2 <= r*r 
# apply mask and inverse DFT 
fshift = dft_shift * mask 
fshift_mask_mag = 2000 * np.log(cv2.magnitude(fshift[:, :, 0], fshift[:, :, 1])) 
f_ishift = np.fft.ifftshift(fshift) 
img_back = cv2.idft(f_ishift) 
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray') 
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 2), plt.imshow(magnitude_spectrum, cmap='gray') plt.title('After FFT'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 3), plt.imshow(fshift_mask_mag, cmap='gray') plt.title('FFT + Mask'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 4), plt.imshow(img_back, cmap='gray') plt.title('After FFT Inverse'), plt.xticks([]), plt.yticks([])
plt.show()

程序运行结果如下图所示：

可以看出，高通滤波器阻止了所有的低频信号，并且仅允许高频通过。由于边缘通常是由高频信号构成的，因此可以在最后的图像中找到原图像的边缘信息。

审核编辑：汤梓红