五次多项式插值法
五次多项式有6个待定系数,可同时对起始点和目标点的角度、角速度和角加速度给出约束条件。
数学推导


MATLAB代码
%五次多项式插值法
clear;
clc;
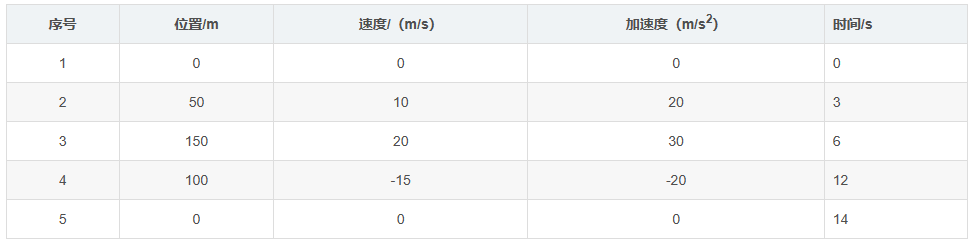
q_array=[0,50,150,100,40];%指定起止位置
t_array=[0,3,6,12,14];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
a_array=[0,20,30,-20,0];%指定起止加速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[a_array(1)];%初始状态
for i=1:1:length(q_array)-1%每一段规划的时间
T=t_array(i+1)-t_array(i);
a0=q_array(i);
a1=v_array(i);
a2=a_array(i)/2;
a3=(20*q_array(i+1)-20*q_array(i)-(8*v_array(i+1)+12*v_array(i))*T-(3*a_array(i)-a_array(i+1))*T^2)/(2*T^3);
a4=(30*q_array(i)-30*q_array(i+1)+(14*v_array(i+1)+16*v_array(i))*T+(3*a_array(i)-2*a_array(i+1))*T^2)/(2*T^4);
a5=(12*q_array(i+1)-12*q_array(i)-(6*v_array(i+1)+6*v_array(i))*T-(a_array(i)-a_array(i+1))*T^2)/(2*T^5);%计算五次多项式系数
ti=t_array(i):0.001:t_array(i+1);
qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3+a4*(ti-t_array(i)).^4+a5*(ti-t_array(i)).^5;
vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2+4*a4*(ti-t_array(i)).^3+5*a5*(ti-t_array(i)).^4;
ai=2*a2+6*a3*(ti-t_array(i))+12*a4*(ti-t_array(i)).^2+20*a5*(ti-t_array(i)).^3;
t=[t,ti(2:end)];q=[q,qi(2:end)];v=[v,vi(2:end)];a=[a,ai(2:end)];
end
subplot(3,1,1),plot(t,q,'r'),xlabel('t/s'),ylabel('p/m');hold on; plot(t_array,q_array,'o','color','r'),grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t/s'),ylabel('v/(m/s)');hold on;plot(t_array,v_array,'*','color','r'),grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t/s'),ylabel('a/(m/s^2)');hold on;plot(t_array,a_array,'^','color','r'),grid on;
% 指定文件夹保存图片
filepath=pwd; %保存当前工作目录
cd('C:UsersAdministratorDesktoppic') %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:UsersAdministratorDesktoppicwu.jpeg'); %将图片保存为jpg格式,
cd(filepath) %切回原工作目录

两种插值法的效果对比
相对于三次多项式插值, 五次多项式插值法所得到的轨迹加速度也是平滑的曲线,并没有出现跳变的情况。
在机器人系统中,关节角加速度出现跳变现象意味着关节的电机会受到冲击, 因此为保证电机平稳运行,角加速度要求平滑连续。
虽然三次多项式插值法的计算量和较之更小,但对于离线规划而言,该时间成本可以忽略,因此从规划的轨迹平稳度而言,五次多项式插值法更佳。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
matlab
+关注
关注
185文章
2974浏览量
230407 -
机器人
+关注
关注
211文章
28390浏览量
206953 -
机械臂
+关注
关注
12文章
513浏览量
24557
发布评论请先 登录
相关推荐
MATLAB多项式函数命令
MATLAB多项式函数命令Roots 求多项式根 Poly 构造具有指定根的多项式 Polyvalm 带矩阵变量的多项式计算 Residue 部分分式展开(留数计算) Polyfit
发表于 09-22 16:01
想用labview进行公式计算,请问是怎么实现上面是常数下面是多项式这种形式的多项式的运算?
本帖最后由 一只耳朵怪 于 2018-5-21 11:23 编辑
想用labview进行如图所示的公式计算,我找到了多项式插件,但是没研究明白怎么实现上面是常数下面是多项式这种形式的多项式的运算,不知道能否请各位大佬指点一
发表于 05-21 11:03
6自由度机械臂点到点5次多项式插值轨迹规划
([0 0.515 0pi/20]);L5=Link([pi00pi/20]);L6=Link([0 0.08000]);[q ,qd, qdd]=jtraj(q1,q2,50); %五次多项式轨迹,得到关节角度,角速度,角加速
发表于 03-13 10:09
基于拉格朗日插值多项式的光伏电池I-V特性建模方法
本文提出了一种基于拉格朗日插值多项式的光伏电池I-V特性的新的建模方法。该方法利用桑迪亚(Sandia)国家重点实验室I-V特性曲线上的五个点的值
发表于 01-04 17:13
•22次下载
正交多项式拟合-matlab
正交多项式拟合:给定函数f(x)在m个采样点处的值f(xi)以及每个点的权重wi,求曲线拟合的正交多项式Pn(x)满足最小二乘误差||err||2=∑mi=1wi[f(xi)−Pn(xi)]2《TOL。
发表于 11-27 15:29
•7919次阅读
六自由度机械臂三次多项式插值法
对串联机械臂而言,轨迹规划可以分为:关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划是把机器人的关节变量变换成跟时间的函数,然后对角速度和角加速度进行约束。 笛卡尔空间轨迹规划是把机器人末端在




 机械臂五次多项式插值法介绍
机械臂五次多项式插值法介绍










评论