导读:文章从8个小节详讲,分为,1.关于Smith圆图;2.等反射系数圆;3.等反射系数圆的分析;4.归一化阻抗圆;5.电阻圆;6.电抗圆;7.完整的Smith阻抗圆图总结;8.导纳圆图。
1.关于Smith圆图
Smith圆图是1939年由P.Smith在贝尔电话实验室工作时开发的。
史密斯圆图由两族圆组成:等反射系数圆、归一化阻抗圆图。归一化阻抗圆又包含了电阻圆、电抗圆两种。
2.等反射系数圆
首先线上任意一点的反射系数等于下式:
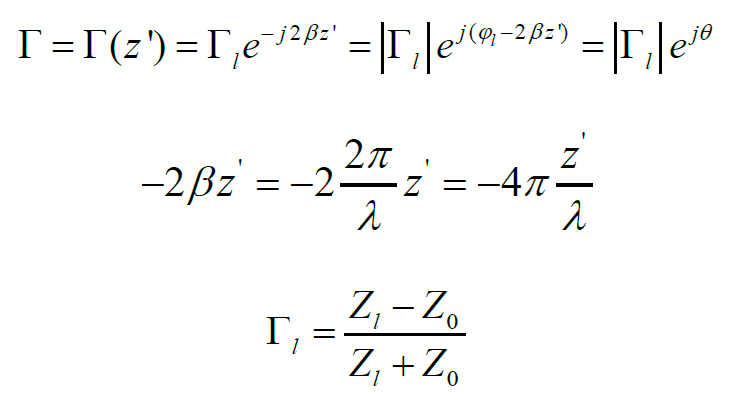
注意:典型的传输线系统如下,只要写的是z’,表示的是从负载端为坐标起点。另外z’/λ也就是电长度。
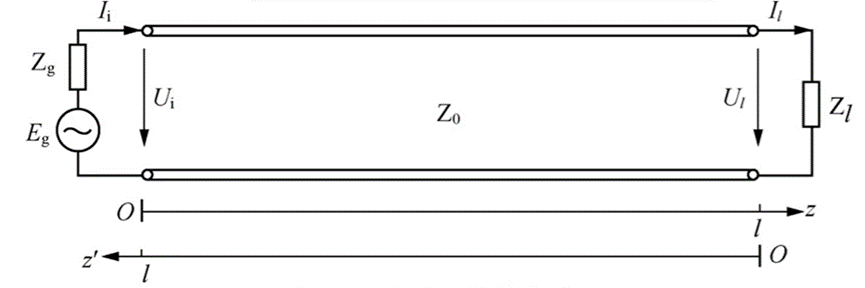
上面的反射系数式子,用实部和虚部的形式表示为:
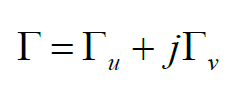
用模的形式表示,有:
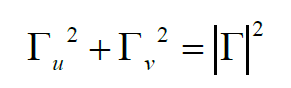
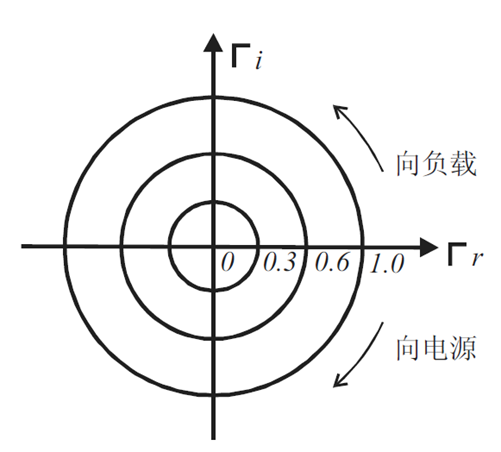
如果以Гu为横轴(可以理解为x轴),Гv为纵轴(可以理解为y轴),画图,那么上式就就是以原点为圆心,反射系数的幅值|Г|为半径的圆。这个圆就是等反射系数圆。如下图:
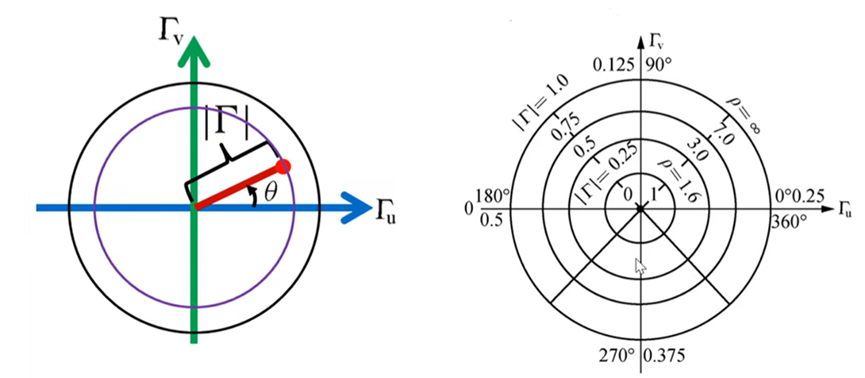
3.等反射系数圆的分析
根据反射系数的计算公式:
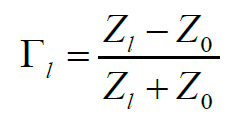
当终端短路时,即Zl=0。此时反射系数Гl就为-1。-1也就是1ejπ。所以,短路点在坐标轴中的位置为(-1,0),即实部为-1,虚部为0,在圆图中的最左边的一点。
当终端开路时,即Zl为无穷大,根据上式两个相等的无穷大比值就为1。此时反射系数Гl就为1。1也就是1ej0。所以,开路点在坐标轴中的位置为(1,0),即实部为1,虚部为0,在圆图中的最右边的一点。
当终端接负载等于传输线特性阻抗(Z0=Zl),此时反射系数就为0。所匹配点在圆心(0,0)的位置。
因为反射系数的模值范围是:0≤|Г|≤1,所以等反射系数圆是一族以原点为圆心的同心圆,最小圆的半径为0,此处为匹配点。最大圆的半径为1,这个圆代表着全反射。
再根据下式来分析幅角θ。θ是从坐标原点出发,终止于单位圆的射线,并规定单位圆与正实轴的交点为θ=0°,从该点逆时针方向旋转一周,θ从0°增加到360°。
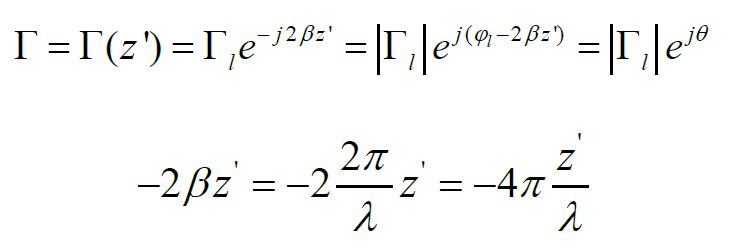
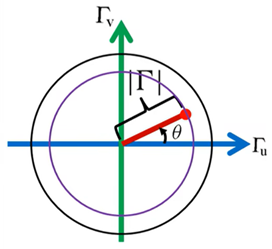
反射系数的幅角的变化与传输线上两点间的电长度△z’/λ有关,因此通常可以用电长度来表示幅角。当z’=λ/4时,幅角-2βz’就等于-π。因此,半个圆周就相当于0.25λ,整个圆周相当于0.5λ。
另外,z’为正的时候,幅角θ为负数,也就是顺时针。注意前面说过,只要写的是z’,表示的是从负载端为坐标起点。所以,在圆图中顺时针转的时候,就是从负载向电源端转,逆时针就是向负载转。
4.归一化阻抗圆
实际的阻抗等于下式,注意Zc是特性阻抗,有时也用Z0表示,一般无耗传输线用Zc。
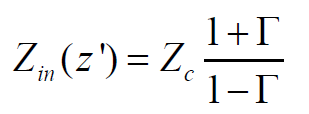
归一化的阻抗写成下式:
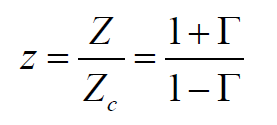
反射系数Г在前面已经用下式表示:
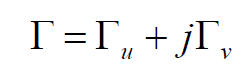
所以把上式代入到z,就可以得到z关于Гu和Гv的等式。将z也写成实部和虚部的形式:
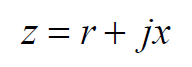
其中,把代入后得到的r和x值求出来,得到:
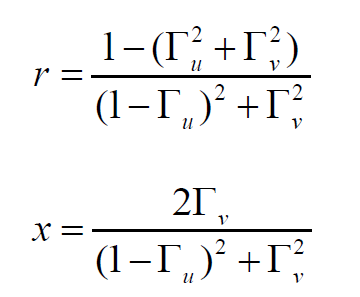
把上面两个式子,再整理一下,就有了以下的式子:
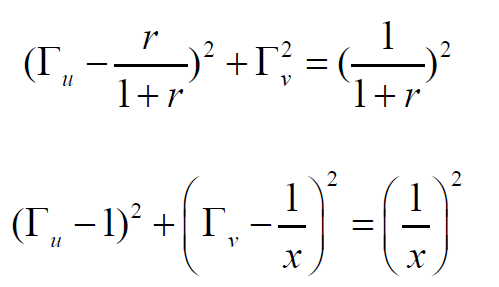
还是以Гu为横轴,Гv为纵轴,这两个方程都是圆的方程。画圆,当归一化的电阻r取不同常数时,第一个式中画出来的一族圆,就称为归一化电阻圆,第二个式子画出的圆为电抗圆。
5.电阻圆
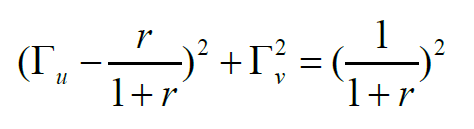
当Гu =1,Гv=0时,上式恒成立。所以不管r等于多少,这些圆都恒过(1,0)坐标点。
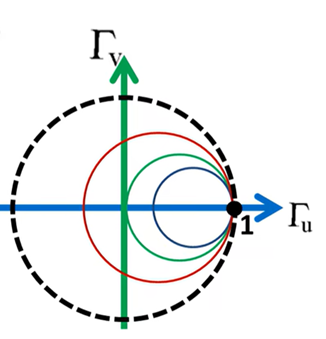
分析电阻圆的公式,圆心为(r/(1+r),0),半径为1/(1+r)。r越大,对应的等电阻圆的半径就越小。电阻r的范围是0≤r<∞。
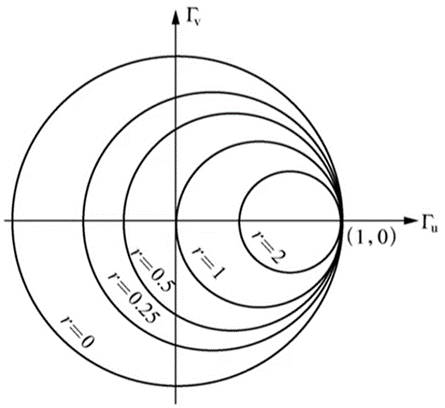
6.电抗圆
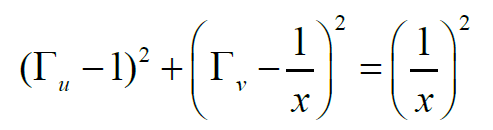
圆心为(1,1/x),半径为1/|x|,注意电阻r不可能有负的电阻,但x可正可负。x为正,代表感性,x为负,代表容性。所以可以画出来两组,而且恒过(1,0)点,如下所示:
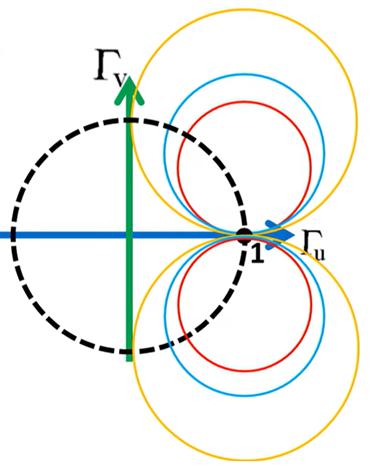
由于反射系数的限制,所以上图彩色圆的部分只有虚线内的才是可以用的。所以得到的电抗圆图如下所示:
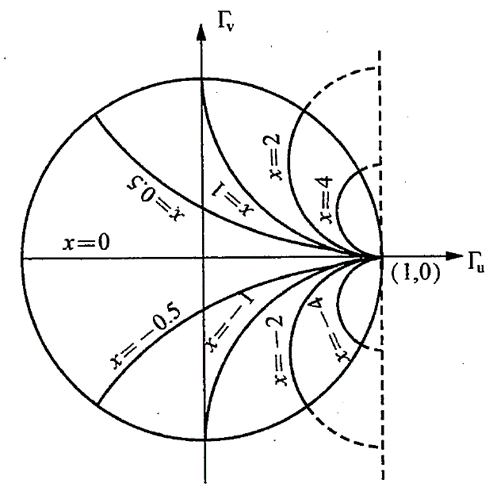
7.完整的Smith阻抗圆图总结
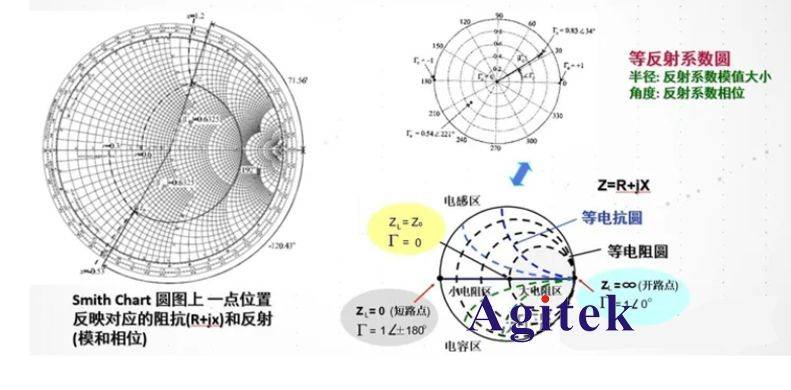
将上述的等反射系数圆、等归一化的电阻圆、等归一化的电抗圆重叠在一起,就构成了完成是阻抗圆图,又称史密斯圆图。
根据以上对圆图构成的分析,可以得到以下的结论:
(1)圆图的中心点对应于Г=0,r=1(即Zl=Zc),x=0,ρ=1,是匹配点。
(2)实轴上的所有点(两端点除外)表示为纯归一化电阻。这是因为当x等于0时,电抗圆的半径为∞,等电抗圆退化为实轴。
(3)实轴左端点对应的Г= -1,z=0,故该点是短路点。
(4)实轴右端点对应的Г= 1,z=∞,故该点是开路点。
(5)圆图的单位圆对应于Г= 1,r=0,z = jx,所以该圆为纯归一化电抗圆。
(6)实轴以上x>0,所以上半圆各点代表各种不同数值的感性阻抗。
(7)实轴以下x<0,所以下半圆各点代表各种不同数值的容性阻抗。
(8)圆图的右半实轴(幅角θ=0°)上的点对应于传输线上电压的同相位点,所以的电压波腹点(电流波节点),r的值即为电压驻波系数ρ的值。左半实轴对应电流波腹点(电压波节点),即电流的同相位点。
(9)圆图最外圈标有电长度的刻度,阻抗圆图上的电尺寸刻度的起算点在实轴的左端点。圈外刻度顺时针转,即“向波源方向”。逆时针转,是“向负载方向”。
(10)串联电感:顺时针沿电阻圆移动。
因为电感和电容都只影响复阻抗,所以实部电阻是不变的,仍然在恒阻圆上。同时,电感的感抗jωL为正,串联电感,电感增大,感抗增大。由于电抗圆中,顺时针的感抗是增大的(可看上面电抗圆图中x=0.5,x=1,x=2,x=4的位置,顺时针时候感抗是增大的),所以串联电感是沿着电阻圆、顺时针转。
(11)串联电容:逆时针沿电阻圆移动。
串联电容,电容是减小的,容抗减小(负的更多了),所以逆时针转。
(12)并联,一般在导纳圆图中转,具体见下文的导纳圆图。此时:
并联电感:沿着电导圆、逆时针移动。
并联电容:沿着电导圆、顺时针移动。
8.导纳圆图
传输线上并联元件或并联分支线,用导纳计算要比阻抗计算方便,用于导纳计算的圆图称为导纳圆图。
因为导纳Y是阻抗Z的倒数,所以传输线上归一化的导纳为:
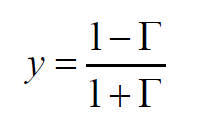
上式也可写做:
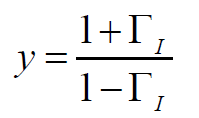
这个式子和阻抗圆图的表达形式完全一样,只是将原来电压反射系数Г换成了电流反射系数ГI。因此,导纳圆图和阻抗圆图的图形完全相同,只是将阻抗圆图作为导纳圆图使用时,应将阻抗圆图中的r、x和Г相应地换位g,b和ГI。
在将阻抗圆图作为导纳圆图使用时,因为ГI= -Г,所以原来阻抗圆图实轴上的电压波腹点和电压波节点的位置,在导纳圆图实轴上分别是电压波节点和电压波腹点的位置。原来阻抗圆图上的开路点和短路点的位置,在导纳圆图上对应短路点和开路点的位置。原来阻抗圆图上的电尺寸刻度的起算点在实轴的左端点,在导纳圆图上在实轴的右端点。两圆图的匹配点都是左边原点。
另外可在圆图上由归一化的阻抗求归一化的导纳。当位置z’=l时,阻抗和导纳有下列的等式:
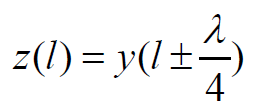
所以传输线上任意点z’=l处的归一化输入阻抗与间隔λ/4位置处的归一化导纳是相等的。所以可在阻抗圆图上找到阻抗对应的点,沿着等反射系数圆将此点旋转180°,相当于z’变化了λ/4,就得到了导纳对应的点值。
编辑:黄飞
-
阻抗
+关注
关注
17文章
961浏览量
46418 -
传输线
+关注
关注
0文章
377浏览量
24198 -
串联电感
+关注
关注
0文章
29浏览量
8102 -
Smith
+关注
关注
0文章
20浏览量
9043
原文标题:一文彻底读懂Smith圆图
文章出处:【微信号:射频美学,微信公众号:射频美学】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
Smith圆图是什么?Smith圆以及阻抗匹配介绍
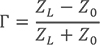




 完整的Smith阻抗圆图总结
完整的Smith阻抗圆图总结










评论