程序实现:
在MATLAB中可采用的语法为:
[K,S,P] = lqr(sys,Q,R,N)
[K,S,P] = lqr(A,B,Q,R,N)
也就是说,目的是计算最佳增益矩阵K
下面以一个例子实现LQR的解法;
M = 85.5; %input 1
m = 8.5; %input 2
b = 0.6;
I = 0.008;
g = 9.8;
l = 0.5;
x0 = [0.2 0 0 0];
a1 = 1;
a2 = 2;
Q = 20;
R=10;
%states = {'x' 'x_dot' 'phi' 'phi_dot'};
p = I*(M+m)+M*m*l^2; %denominator for the A and B matrices
A = [0 1 0 0;
0 -(I+a2*l^2)*b/p (a2^2*g*l^2)/p 0;
0 0 0 1;
0 -(a2*l*b)/p a2*g*l*(a1+a2)/p 0];
B = [ 0;
(I+a2*l^2)/p;
0;
a2*l/p];
[K,S,P] = lqr(A,B,Q,R)
运行可以得到:
K =
-1.4142 -62.4810 67.4838 187.5249
S =
1.0e+05 *
0.0088 0.1913 -0.0265 -0.1230
0.1913 7.3677 -1.0374 -4.8827
-0.0265 -1.0374 0.5767 1.7582
-0.1230 -4.8827 1.7582 5.9016
P =
-0.0262 + 0.0258i
-0.0262 - 0.0258i
-0.4016 + 0.0093i
-0.4016 - 0.0093i
程序可视化:
sys = ss(A,B,eye(4),[0;0;0;0]);
sysclosed = ss(A-B*K,[0;0;0;0],eye(4),[0;0;0;0]);
figure(15)
[ycl,tcl,xcl] = initial(sysclosed,x0);
plot(tcl,ycl(:,1),tcl,ycl(:,2),tcl,ycl(:,3),tcl,ycl(:,4))
title('LQR ')
xlabel('时间')
ylabel('输出')
legend('x','x_dot','phi','phi_dot')

LQR 启发式作为基于样本的运动规划算法(例如 RRT 或 RRT*)的扩展,可以是相对低成本的距离度量,并在具有复杂或欠驱动动态的域中找到最佳计划。
% LQR Steer
%===================================
function x_new = LQRSteer( x_nearest, x_rand, K_rand )
% This function contains system's explicit dynamics
global model;
m = model.phy.m;
l = model.phy.l;
b = model.phy.b;
g = model.phy.g;
h = model.h;
u = -K_rand*( x_nearest - x_rand )';
x_dot = [ x_nearest(2), ( u - b*x_nearest(2) - m*g*l*sin(x_nearest(1)) ) ];
x_new = x_nearest + x_dot*h;
end
此MATLAB function可以从来执行系统动力学描述;
% LQR Near
%===================================
function X_near_ids = LQRNear( x_new, S_new, id_nearest )
global GNodes nun;
% Define Neighborhood Radius
gamma = 1; d = 2;
ner = gamma*( log(nun+1)/nun )^(1/d);
% Allocate and Assign to Output
X_near_ids = id_nearest;
for i = 1 : nun
x = GNodes( i, 1:2 );
cost = (x-x_new)*S_new*(x-x_new)';
if cost < ner
X_near_ids(end+1) = i;
end
end
X_near_ids = unique(X_near_ids);
end
输入期望的初始参数,根据定义算法的逻辑可实现期望数值的求解;
线性二次高斯(LQG)优化控制设计方法,它是线性二次估计器(LQE)(即卡尔曼滤波器)和线性二次调节器(LQR)的组合。
对于逆最优问题,建议读者阅读 Zhifei 和 Joo的文章。最优控制理论的逆问题通过二次逼近 (BOBYQA) 技术 的边界优化来适应和解决。
人工操作任务的成本函数是从给定的演示中建模的,同时考虑与环境的接触。引入逆Karush-Kuhn-Tucker(KKT)逆最优控制算法来学习具有接触约束的操纵任务的成本函数。
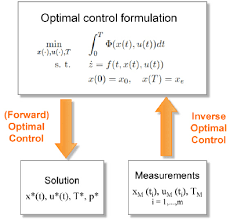
最优控制理论的主要关注点是找出在满足某些最优标准的同时将给定系统推向所需状态的控制信号。
线性二次调节器 (LQR) 是优化控制的一种变体,其中系统动力学由一组线性微分方程建模。此外,最优标准由包含系统状态和输入的二次函数描述。
考虑智能体之间的关系,也可以用LQR来求解出最优解;
寻找规定机器人阻抗模型的最佳参数的问题被转化为线性二次调节器 (LQR) 问题,该问题最大限度地减少了人力并优化了 HRI 系统针对给定任务的闭环行为。
为了避免对人体模型知识的要求,可以使用积分强化学习来解决给定的 LQR 问题。
-
matlab
+关注
关注
185文章
2974浏览量
230448 -
机器人
+关注
关注
211文章
28413浏览量
207036 -
最优控制
+关注
关注
0文章
9浏览量
7143
发布评论请先 登录
相关推荐
主动队列管理建模及最优控制策略
什么是工业机器人
辰汉-如何实现服务机器人的运算与控制
基于Matlab和VR技术的移动机器人建模及仿真
大纯滞后对象的最优控制
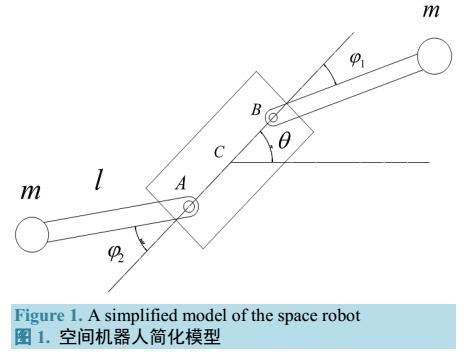
基于Legendre伪谱法的空间机器人姿态运动的最优控制
使用Matlab和VR技术实现移动机器人的建模及仿真的方案说明
如何使用Matlab和VR技术实现移动机器人的建模和仿真




 机器人最优控制的程序实现
机器人最优控制的程序实现










评论