超导量子比特的基本原理及结构特征

文章来源：中国物理学会期刊网 原文作者：郑文 于扬

超导量子计算核心器件，是量子计算的关键。它以其独特的超导性质，为我们打开了探索量子世界的大门。

摘要

算力是数字经济时代新的生产力。量子计算基于量子力学的规律进行计算，人们普遍相信它可以在不久的将来在某些问题上完成经典计算机所无法完成的计算任务，实现量子优越性。作为最有可能实现通用量子计算的平台之一，以约瑟夫森结为核心元件的超导量子比特，在量子控制和量子测量方面具有稳定、可靠、便于设计和扩展等独特的优势，受到科学界甚至产业界的广泛关注，正在高速发展。文章围绕约瑟夫森结这一具有非线性和无耗散特征的超导量子器件，阐述了超导量子比特的基本原理及结构特征，重点介绍超导量子芯片设计、加工方面的前沿进展，并对未来发展方向进行简单的展望。

01引 言

现代信息社会的进步离不开计算机芯片日新月异的发展。在20世纪50年代左右，科学家们找到了一种性能优越、成本低廉的芯片计算单元——硅半导体晶体管。此后按照摩尔定律，晶体管集成度每18个月增加1倍，造就了蓬勃发展的数字经济时代。如今集成电路芯片最先进的制程已经实现3 nm并开始迈入2 nm制程。在该尺度下，材料中微观原子的量子效应成为芯片继续发展的瓶颈，导致摩尔定律不再适用。于是，人们开始寻找新的计算方式，其中就包括量子计算。

区别于经典计算机芯片中的计算单元是用晶体管的两种不同状态实现0和1的二进制编码计算操作，量子芯片中量子比特是依据量子态可以处于0和1的相干叠加状态，进行量子操控。根据量子力学原理，N个比特就可以对2N个叠加的数同时进行并行运算。量子芯片独特的性质预示着量子计算在数字经济时代有着潜在的巨大优势。如今，面向大规模集成的量子芯片也在寻找属于自己的“量子晶体管”，基于约瑟夫森结的超导量子比特就是最有希望的候选者之一。

超导量子计算发展至今已有二十余年，得益于在芯片设计、加工制备和测试封装等方面的独特优势，已在随机线路采样方面实现了量子优势[1，2]。特别地，以谷歌和IBM为代表的科技公司提出：在近十年内构筑百万比特量级的超大规模超导量子处理器，最终实现以量子计算为中心的超级计算。此外，其他传统科技公司如阿里巴巴、华为、腾讯，或初创公司如Rigetti、IQM、量旋、本源量子等也加入到超导量子计算这一赛道。超导量子计算初步形成产业链雏形，带动着上下游产业的发展。然而，要实现通用量子计算机，超导量子比特依然面临着相干时间不够长、测控精度不够高、扩展规模不够大等挑战。本文将从超导量子芯片的基本结构出发，简要介绍超导量子比特的基本原理和特性，解析超导量子比特在优化结构设计、改进扩展封装和提高测控技术等方面的发展现状，评述超导量子比特在实现通用量子计算过程中所具有的独特优势以及面临的挑战。

02约瑟夫森结

超导量子比特可以作为“量子晶体管”的候选者，其核心器件是具有非线性、无耗散特点的约瑟夫森结。如图1(a)所示，约瑟夫森结的经典结构是S(超导体)—I(绝缘层)—S(超导体)“三明治”结构。目前在超导量子比特中，常用的约瑟夫森结以金属铝为超导材料，铝的氧化物为绝缘层，具有工艺加工简单、稳定等特点。

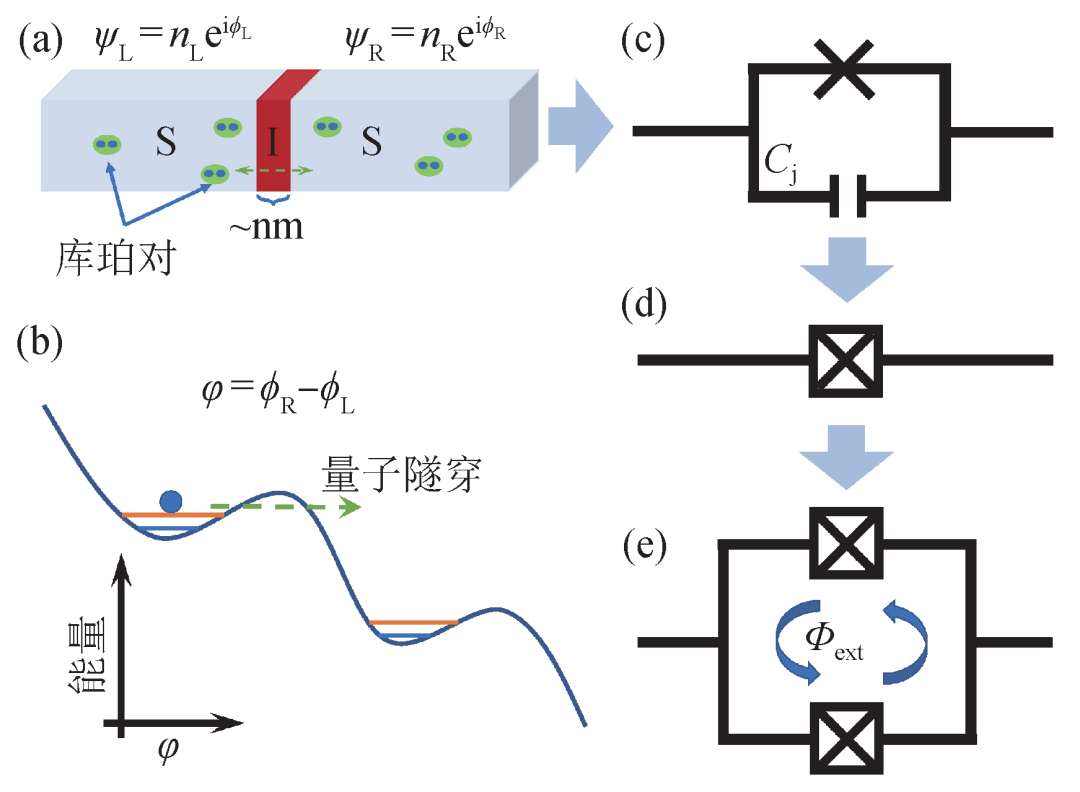
图1 约瑟夫森结的结构及原理 (a)约瑟夫森结的“三明治”结构示意图，包括两层超导体和中间很薄的绝缘层。超导体中库珀对凝聚的量子基态用波函数ψLR表示;(b)在偏置电流Ib作用下，约瑟夫森结等价于一个质量为m的“人造原子”在势能U中运动。当Ib≪Ic，“原子”被很好地囚禁在单个势阱内，具有不等间距的量子能级。当Ib接近于Ic时，“原子”将因为量子隧穿等逃逸出势阱;(c)理想约瑟夫森结一般用“×”表示，可以等效为非线性电感Lj，实际中还包含一个电容Cj;约瑟夫森结在电路图中通常用(d)图的符号来表示;(e)由两个约瑟夫森结形成环路的DC-SQUID结构示意图

根据BCS理论，超导体中的电子会结成库珀对，凝聚到一个宏观基态，可以用波函数ψLR(t)=nLR(t)eiϕLR(t)表示，其中概率幅nLR(t)的模平方正比于库珀对密度，ϕLR(t)是规范相位。该结构的中间绝缘层大约在1—3 nm，两端超导体之间形成一个弱连接，所对应的波函数有交叠，库珀对可以量子隧穿通过绝缘层，在约瑟夫森结中形成超导电流I。这种结构中会出现两种现象[3，4]。

(1)直流约瑟夫森效应。当外加电压V=0，且电流小于临界电流Ic，绝缘层两端始终保持零电压现象，整个系统则一直处在无电阻状态，并且超导电流满足关系式I=Icsinφ，这里相位是绝缘层两侧超导体波函数之间的相位差φ=ϕR-ϕL。

(2)交流约瑟夫森效应。在约瑟夫森结两端施加直流电压V，此时超导相位φ会随着时间发生变化，结两端电压的关系满足

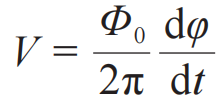
，其中Φ0=2.0678×10-15 Wb为磁通量量子。由直流约瑟夫森关系，绝缘层两端超导体中的库珀对隧穿电流变为高频交变电流，频率与施加的直流电压成正比。

显然，如果超导电流对时间求导，很容易得到

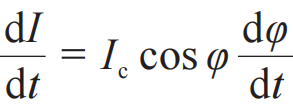
。再由法拉第电磁感应定律，类比普通电感公式

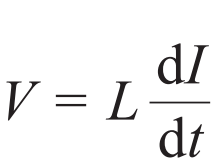
，可以得到一个有效电感为

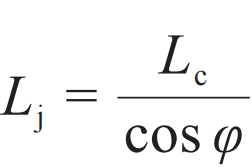
，其中

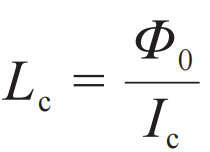
。不同于普通器件的电感系数是一个恒定值，约瑟夫森结等效的电感会随着绝缘层两端超导体相位变化而非线性变化。于是，如图1(b)所示，可以通过调控超导相位实现系统特殊能级结构的设计，再依据调控特定的参数(如环路磁通、超导相位、库珀对数目等)，实现超导量子比特。

此外，“三明治”结构本身会有一个电容Cj产生，如图1(c)所示(通常简化为图1(d))，约瑟夫森结可以看作是一个非线性电感Lj并联电容Cj的LC振荡电路系统。在超导量子芯片中，通过经典的电路分析建立起系统的拉格朗日量，再通过引入正则量子化，根据量子力学可以研究整个系统的量子行为。值得注意的是，如图1(e)所示，当两个约瑟夫森结并联形成环路时，可以构成直流超导量子干涉器件(DC-SQUID)。如果引入一个外部磁通Φext，环路中磁通量的变化将改变DC-SQUID等效的电感大小。这样的特征使得DC-SQUID在超导量子计算和弱磁信号探测等方面有着丰富的应用[5—10]。

03超导量子比特基本类型

一般来说，超导量子比特有三种基本类型：电荷比特、磁通比特和相位比特。这是由于实现量子比特的宏观物理量分别是库珀对数目变化、环路超导电流方向和偏置电流大小(即相位φ大小)。三种类型的超导量子比特需要设计相应的电路结构实现特定的约瑟夫森能Ej、电荷能Ec和电感能El。接下来，我们将具体介绍三种量子比特的基本特征。

(1)电荷比特。首先是日本电气股份有限公司(NEC)的研究人员在1999年从实验上观测到量子态的相干振荡[11]。该比特也被称为库珀对盒子(Cooper-pair box)，如图2(a)所示，是单独的一个约瑟夫森结，其中一端接地，另一端通过栅极电容Cg耦合外部信号源，可以调节栅极电压Vg，以改变栅极电容上感应的极化电荷ng=CgVg/2e。该比特的约瑟夫森结要足够小，整个系统的电荷能

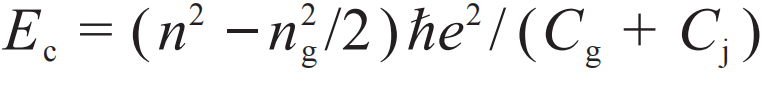
远大于约瑟夫森能Ej，没有电感能，即Ej/Ec≪1，El=0。其中，n为超导岛上的库珀对数量，是一个离散的变量。相邻的库珀对数目状态

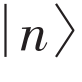
和

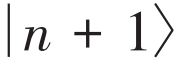
定义为量子比特状态

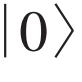
和

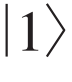
。虽然n是一个整数，但ng是一个连续变量，通过改变栅极电压控制超导岛上库珀对数目的变化，实现比特状态的控制。在实验中，电荷噪声影响ng导致很难实现长的相干时间。在当时的实验条件下，量子态相干时间仅有纳秒量级。2002年，通过设计更大的约瑟夫森能Ej/Ec≃1，对电荷比特在控制和读取方面做了改进，在噪声不敏感点做量子操控，实现超导电—磁混合量子(quantronium)比特[12]，相干时间达到微秒量级。

图2 常见的超导量子比特类型 (a)实验上首次实现电荷比特的库珀对盒子[11];(b)实验上实现超导磁通比特的照片及其调控示意图[17];(c)实验上观测到的相位比特的相干振荡，其中Ω1和Ω2代表量子态相干振荡圆频率[20];(d)实验上实现准电荷比特的样品图，左上图片是等效电路图[25]

(2)磁通比特。最初源于Leggett在1984年期间提出[13，14]用射频超导量子干涉器件(RF-SQUID)来观测磁通态之间宏观量子相干振荡，2000年Friedman等人在实验上观测到了量子相干叠加[15]。但是受到关注的磁通比特是1999年代尔夫特理工大学的研究团队理论上提出[16]，在2003年实验上实现[17]的超导恒流(persistent-current)量子比特，如图2(b)所示。它是由包括一个小的约瑟夫森结和两个大的约瑟夫森结的超导环路组成，约瑟夫森结的作用是形成一个大的等效电感代替几何电感，减小了整个电路的面积，从而降低环境对量子比特的影响，增加相干时间。此时系统满足条件El/Ej~1，Ej/Ec≫1。将环路中电流的顺时针和逆时针方向定义为量子比特状态，通过控制环路超导电流的方向实现对量子比特的操控。由于比特对磁通噪声很敏感，稍微远离最佳位置，磁通比特的相干时间就会显著缩短[18，19]。

(3)相位比特。该比特由一个较大的约瑟夫森结组成，使系统满足条件Ej/Ec远远大于1。不同于电荷比特中库珀对数目的变化和磁通比特中环路电流的方向定义量子比特，该比特只需要调控很小的超导电流变化，即可以用约瑟夫森结两端的规范相位φ变化描述该系统，所以被称作相位比特。如图2(c)所示，相位比特首先在2002年由美国堪萨斯大学研究团队实验上观测到微秒量级长时间的相干振荡[20]，之后加州大学圣巴巴拉分校的研究团队也观测到该类型比特的相干振荡[21]。这种比特可以调控出一个亚稳势阱，势阱内只有几个能级，将其中最低的两个能级定义为量子态

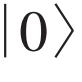
和

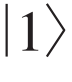
。势阱内能级越高的占据数，发生隧穿的概率越大。然而，与其他比特不同，当占据数离开亚稳态势阱时，作为计算基矢的希尔伯特空间被破坏，因此该比特显著的缺点是不适合非破坏性测量。相应地，它的优点是由于隧穿效应，量子态测量的信噪比很高。

在21世纪初，电荷比特、磁通比特的相干时间都很短，相位比特虽然相干时间相对较长，但是在量子态测量方面有着天然的缺陷。在此基础上，结合电路量子电动力学的发展[22—24]，人们通过优化微纳加工工艺和调整电路结构，设计出很多种目前广泛应用的超导量子比特变体。值得注意的是，在2020年，马里兰大学的研究人员通过设计特殊的高阻抗器件，如图2(d)所示，在系统满足El/Ej~1/100，Ej/Ec~1条件下，找到了准电荷(quasicharge)这一宏观物理量描述该系统，实现了第四种类型的布洛赫量子(blochnium)比特[25]。相对于其他类型的超导量子比特，目前该比特对样品加工设计要求苛刻，在今后的超导量子芯片加工设计中是否具有优势还需要实验检验。

04超导量子比特新型结构

为了提高超导量子比特的性能，包括相干时间、测控精度、规模化扩展能力等，人们不断对比特设计进行优化，下面主要介绍目前受到广泛关注的几种新型量子比特。

(1)并联电容的电荷比特。目前大多数超导量子比特结构采用的都是2007年耶鲁大学研究团队提出的超导传输子(transmon)比特[26]，或是在它基础上将约瑟夫森结一端接地实现如图3(a)的X型超导传输子(Xmon)比特[27]。该类型比特是约瑟夫森结并联一个大电容Cs，即Cs≫Cj，此时传统的电荷比特的能量条件变为Ej/Ec≫1。大电容的分流作用会屏蔽结两端极化电荷的漂移，比特能谱对电荷噪声不敏感，可以实现更长的相干时间。目前transmon类型的比特相干时间已经接近毫秒量级[28]。但是transmon类型比特牺牲了能谱的非谐性，限制了高精度量子门操作的速度。

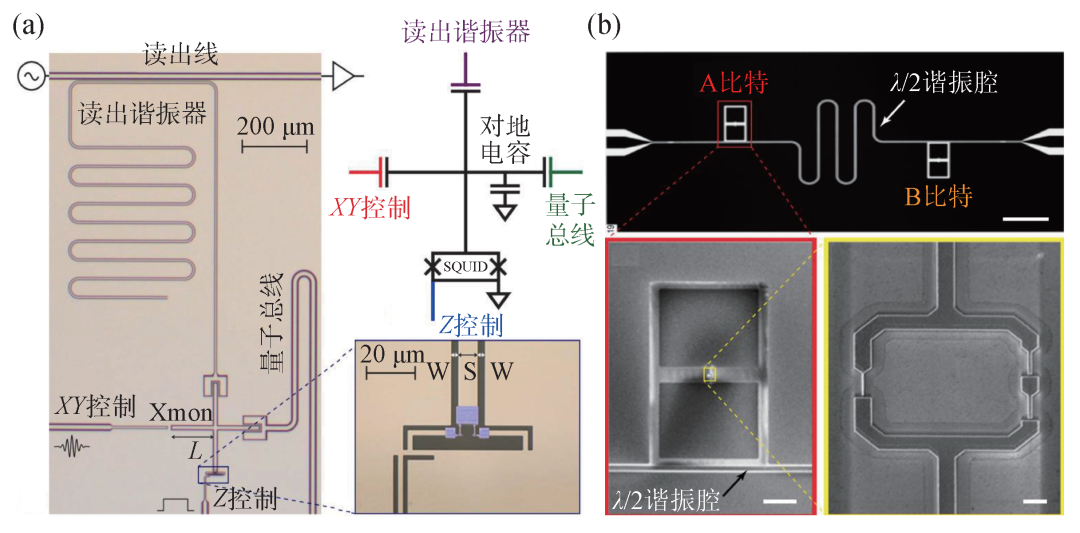
图3 受到广泛关注的超导量子比特 (a)并联大电容的电荷比特，约瑟夫森结一端接地，这种类型的transmon比特也叫作Xmon比特[27]。其中，左图是Xmon样品图，右下图是放大后约瑟夫森区域结构，右上图是相应的电路结构示意图;(b)并联大电容的磁通比特，也称作c-shunt flux qubit[32]。其中，上图为两个并联电容的磁通量子比特通过谐振腔耦合的样品图，下部为放大后比特A的电镜图以及三个约瑟夫森结的电镜图

(2)并联电容的磁通比特。早在2007年，研究人员就提出并联一个电容来解决磁通比特相干时间在非简并点受到磁通噪声影响的问题[29]，不过在2010年，IBM的研究人员首次在实验上实现该比特的相干时间只有微秒量级[30]。接着在2016年，滑铁卢大学[31]和麻省理工学院[32]的研究团队在Φ/Φ0=0.5π偏置点证实，该类型比特(图3(b))拥有transmon比特对电荷噪声不敏感的特点。相较于transmon类型比特，该比特不同约瑟夫森结的参数相差大，在样品加工和磁通调控方面稍显复杂。值得注意的是，随着偏置磁通的变化，这类比特能谱非谐大小会发生变化。因此可以通过合适的参数设计调控比特能谱非谐，这在快速量子门操控和多比特高开关比耦合等方面有潜在的应用。

(3)并联电感的超导电感(fluxonium)比特。2009年耶鲁大学团队提出的fluxonium比特[33]，既可以抑制电荷噪声，同时又有很大的非谐，受到较大关注。它是由一个小型约瑟夫森结与一个大型线性电感L并联而成的环路，其电感能El满足El≪Ej。等效电路结构可以看作是一个约瑟夫森结并联一个大电感，以抑制电荷噪声。因为要保证样品加工中伴随大电感产生的寄生电容Cp足够小，以避免其产生的谐振模式导致结区的相位滑移，一般需要满足条件(L/Cp)1/2≫(Lj/C)1/2∼RQ，其中，RQ=ℏ/(2e)2≃1 kΩ。由于现实中最大真空阻抗约为377 Ω，大电感通常用多个大的约瑟夫森结阵列串联实现，这在样品加工中具有一定的挑战性。随着工艺制备和操控技术的提升，最近几年制备如图4(a)所示的fluxonium在长相干时间[34，35]、高保真度门操控[36，37]和规模化扩展上具有一定的竞争力。

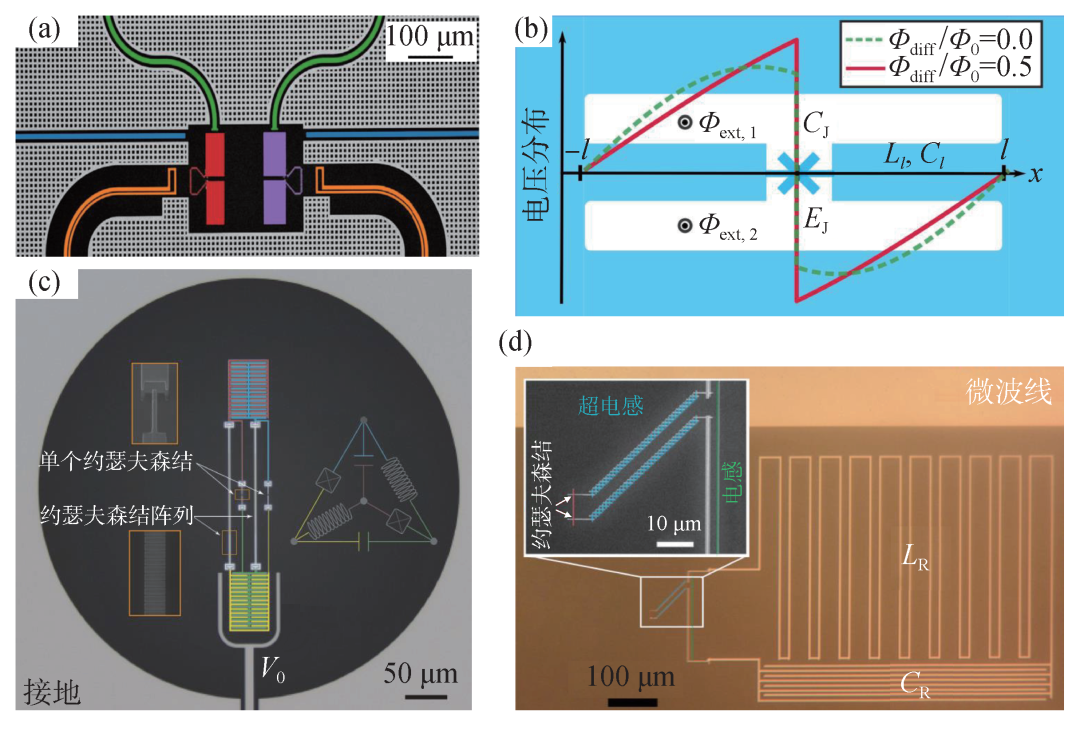
图4 其他类型的新型超导量子比特 (a)fluxonium两比特耦合样品图[37];(b)unimon比特示意图[38];(c)改进参数后实现0—π量子比特的样品图[43];(d)bifluxon比特的样品图[44]

(4)超导酉(unimon)比特。transmon比特相干时间长、样品加工简单，但是非谐小，限制了量子门操控和量子态读取的速度。并联电容的磁通比特和fluxonium比特能够实现较大的非谐，但是样品参数设计和量子操控方式对样品加工有较高要求。在2022年，芬兰大学的研究团队提出如图4(b)所示的unimon比特[38]可以在一定程度上解决上述这些问题。该比特是直接在平面谐振腔中加入单个约瑟夫森结，等效电路图可以看作是transmon并联一个几何电感。约瑟夫森结的作用是对原来谐振模式进行修改，谐振模式提供的电感能远大于结区的电荷能El≫Ej，而谐振模式提供的电荷能改变了整个系统的电荷能，此时该比特与transmon类似满足Ej≫Ec。在一定程度上实现比特在对电荷噪声不敏感的同时也能降低对磁通噪声的敏感程度，并且还可以通过调控磁通调节比特的非谐大小。该比特具有结构设计简单，易于加工制备等特点。不过因为谐振模式的引入，该结构在多比特操控方面是否有优势还有待验证。

(5)0—π量子比特。最近几年，根据改变电路的拓扑结构，量子态具有拓扑保护的超导量子比特受到越来越多研究者的关注。早在2006年，基于约瑟夫森结阵列来实现纠错的研究工作[39，40]，Kitaev提出直接利用约瑟夫森结阵列的电流镜像效应构建具有两种模式、对噪声具有保护作用的0—π量子比特[41]。2013年，Brooks等人[42]进一步研究由四个节点组成的0—π量子比特。这些节点由两个大的超电感L、两个约瑟夫森结和两个大型分流电容C连接。超电感通常由约瑟夫森结阵列构成，可以等效为常规的电感。但是该比特的设计参数在实验上几乎不可能实现。在2021年，普林斯顿大学研究团队通过修改结构的参数，一定程度上首次在实验中演示了图4(c)中的0—π量子比特[43]，并证明了电荷不敏感处量子态对弛豫时间具有指数级保护，同时对磁通噪声引起的相位退相干具有一阶保护作用。这意味着拓扑保护类型的超导量子比特在未来的量子芯片中具有一定的优势。

(6)超导双磁通量子(bifluxon)比特。另外一个受到关注的是2021年由美国罗格斯大学研究团队提出的如图4(d)中具有对称保护的bifluxon比特[44]。该比特在电路结构上结合了quantronium和fluxonium两种量子比特的特点，即由两个参数相同的库珀对盒子，并联一个大电感以分流，形成一个超导环路的对称结构。该结构最初是用来验证Aharonov—Casher(AC)效应[45，46]，即环路中磁通量涡旋(fluxon)随着栅极电荷量ng的调控而相干振荡，并且当ng为奇数时，磁通量涡旋因AC干涉相干相消而不会发生变化[47—49]。因此，通过栅极电压控制超导岛上的电荷以调控环路中磁通量涡旋的变化，定义量子比特状态。显然，因为AC干涉相干相消，磁通量涡旋不发生变化，此时量子态的波函数位于希尔伯特空间的不相交区域，从而抑制能量弛豫。该量子比特实验上相干时间已达到100 μs。

得益于超导量子比特设计和加工的较大自由度，人们提出很多其他类型的超导量子比特，比如通过约瑟夫森结阵列实现拓扑保护的量子比特[50，51]，或结合测量比特能够在一定程度上实现有助于纠错的dual-rail量子比特[52]等。如何在面向规模化扩展的量子芯片中，实现快速的量子操作和量子测量，同时又可以抑制环境噪声对量子比特的影响，是目前超导量子比特结构设计的热点之一。

05超导量子比特耦合结构

实现量子计算需要量子比特之间的耦合。超导量子比特的耦合方式丰富多样，如直接的电容耦合，通过谐振腔实现全局耦合和最近邻耦合，或是利用可调耦合器实现可调耦合等等。在这里，我们简要介绍四种具有高开关比、受到广泛关注的耦合方式。

(1)超导栅控量子比特(gmon)作为耦合器的耦合结构。2011年，加州大学圣巴巴拉分校的研究人员提出，两个相位比特可以通过gmon实现具有高开关比的可调耦合器结构[53]，并在2014年将该结构应用在图5(a)的Xmon比特耦合结构中[54]。该结构将耦合电感引出一个节点和两个比特低电压端连接，在节点之间引入一个约瑟夫森结，通过控制结和地形成回路的磁通以控制两比特之间超导电流的流动，以实现可调耦合。耦合电感Lg远小于量子比特的电感Lj，因此比特能级结构几乎不受耦合结构影响，以保证在规模化扩展中的可复用性。

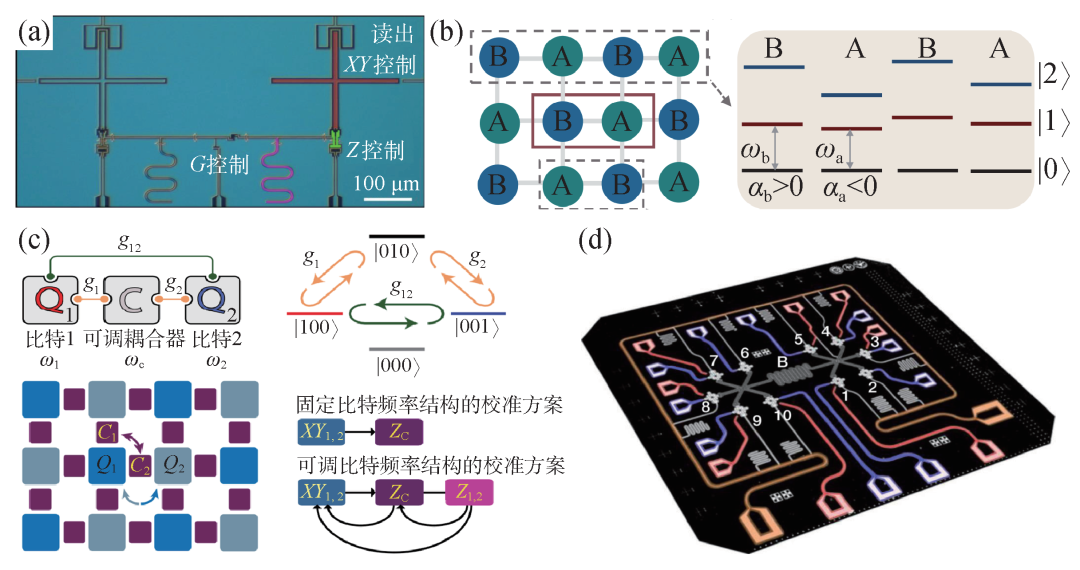
图5 超导量子比特耦合结构 (a)gmon作为耦合器的两比特样品图[54];(b)transmon—flux比特直接耦合结构[55]。其中，左图表示量子芯片中超导传输子比特(A)和并联电容的超导磁通比特(B)空间排布示意图，右图展示的是左侧一个排列单元中AB两种量子比特的最低三个量子能级分布示意图，ωa(ωb)和αa<0(αb>0)表示A(B)类型比特最低两个能级的频率和具有负(正)的非谐;(c)transmon类型比特作为可调耦合器的两比特示意图[56]及其二维平面扩展结构[59]。上部是通过超导传输子比特实现两个比特之间可调耦合的示意图和相应的能级结构示意图，下部是这种耦合结构二维平面结构扩展示意图(左图)，以及固定比特频率和可调比特频率两种调控方式的校准流程图(右图);(d)固定频率的谐振腔作为耦合器的全连通耦合芯片[63]

(2)超导传输子—磁通量子比特(transmon—flux)直接耦合结构。因为transmon比特的非谐是负值，而并联电容的磁通比特的非谐在合适的磁通偏置点附近是正值，并且非谐大小是磁通可调的，于是在2020年，南京大学的研究人员根据这两种比特的独特性质提出直接利用具有正负非谐性的量子比特实现如图5(b)中所示具有高开关比耦合的多比特扩展方案[55]。该结构可以在实现高保真度两比特量子门操控的同时减少耦合器的使用，因此在规模化扩展方面具有减少量子操控线路和减少耗散通道等独特优势。

(3)transmon作为耦合器的耦合结构。随着transmon类型比特的广泛使用，为了样品加工的稳定性，2018年之后，直接用transmon比特作为耦合器[56]来实现高开关比的可调耦合受到广泛的使用。如图5(c)所示，它主要的思想是通过调节耦合器频率控制耦合器与两个比特之间的有效耦合强度g1,2，以线性叠加额外的直接耦合项g12，从而实现具有高开关比的耦合结构。耦合项g12一般可以在两个比特之间直接引入电容实现，或是通过耦合器的电容极板耦合两比特导致的寄生耦合实现[57，58]。2020年，南方科技大学和南京大学的研究人员在实验上验证了这种耦合方式在两比特门高精度操控和扩展方面的优势[59]，如今这种耦合方式已普遍应用在规模化扩展的超导量子芯片中[60]。

(4)谐振腔作为耦合器的全连通耦合结构。通过固定频率的公共谐振腔实现比特之间的耦合[61，62]一直以来都受到人们广泛的关注。特别地，最近几年浙江大学超导量子计算和量子模拟实验团队联合国内外多家单位基于该耦合方式，直接实现了如图5(d)所示的全连通耦合结构的超导量子芯片，利用该耦合结构在多比特纠缠态制备方面已经显示出独特优势，两次打破实现全局纠缠比特数的世界纪录[63，64]。此外，固定频率谐振腔作为耦合器，也可以实现具有高开关比的耦合结构，再结合额外的耦合通道设计和操控方式，可以实现具有高保真度的两比特门操作[65]。

得益于超导量子电路便于设计、加工和操控等特点，还有很多其他重要的耦合结构，如通过超导同轴线缆实现超导量子芯片之间的量子控制[66]。值得注意的是，实现高开关比的耦合不仅可以从结构设计上实现，同时可以结合合适的操控手段，如参量调控、交叉共振等方式实现[67—69]。不过这些方式可能会引入额外的控制波形技术以避免量子态泄露、量子串扰等，弱化了测控的复用性，同时可能面临着难以实现快速的量子门操控等挑战。

06超导量子比特加工技术

超导量子芯片是固态器件，由于结构设计和超导材料的改进，与半导体微纳加工工艺类似，可以通过电路设计和光刻制造技术来大规模生产。但是量子比特的控制和测量通常是单独的微波信号驱动实现，同时约瑟夫森结的尺寸(约100 nm量级)和其他电路结构(大多数是大于等于10 μm量级，包括并联电容、电感以及控制测量电路等)相比相差两个量级以上，这对大规模加工提出新的要求。在这一节中，我们主要介绍目前常见的四种工艺技术。

(1)避免杂散约瑟夫森结产生的绑带(bandage)技术。超导量子比特中的约瑟夫森结制备一般是通过双角度蒸发，但是它会产生不需要的杂散约瑟夫森结，从而导致介电损耗，降低超导量子比特相干时间。最初人们通过引入额外的光刻步骤沉积bandage使得杂散结接地，以改变结的电位[70]，避免对比特相干时间产生影响。2021年，德国卡尔斯鲁厄理工学院[71]和瑞典查尔姆斯理工大学[72]的研究团队分别独立地提出一种改进的原位阴影蒸发技术，实现了在一个工艺步骤中同时加工约瑟夫森结和沉积bandage。如图6(a)所示，这种技术避免了之前方案增加的工艺工序和可能导致的芯片表面污染，适用于目前超导量子芯片的加工生产。

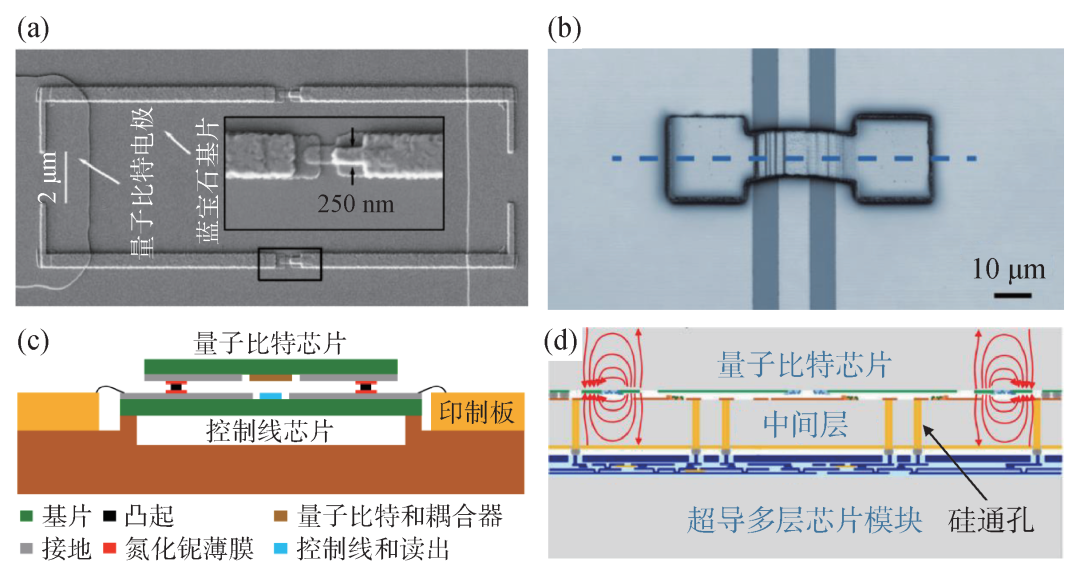
图6 几种规模化加工技术 (a)避免杂散约瑟夫森结的bandage样品图[71];(b)通过梯度曝光实现的空气桥样品图[75];(c)实现量子比特芯片和控制线路芯片连接的倒装焊示意图[77];(d)适用于大数目量子比特芯片集成化的硅通孔示意图[80]

(2)桥接不同空间位置电路结构的空气桥技术。空气桥技术一直以来都是半导体工艺中广泛使用的技术[73]。在超导量子电路中，空气桥对于消除共面波导电路的寄生模式和减少直流磁通偏置之间的串扰等至关重要[74]。2022年，南京大学研究团队发明了一种制造超导空气桥技术[75]，即用单层光刻胶和梯度曝光工艺制备得到图6(b)中的空气桥结构，降低了原有空气桥制造工艺的复杂性，具有高的良品率，同时适用于规模化超导量子芯片的加工生产。

(3)电磁连接不同功能量子芯片的倒装焊技术[76]。该技术通过焊料凸点与基板进行互连，将某一芯片以倒扣的方式电磁连接另一块芯片，可以改善规模化生产中控制线密度不断增加的问题。目前大部分超导量子芯片采用的都是倒装焊技术。如在2022年，瑞典查尔姆斯理工大学研究团队[77]将量子比特芯片和控制芯片用铟凸块连接在一起，如图6(c)所示，系统性地研究了倒装焊对超导量子芯片性能的影响。该技术可以为所有量子比特和耦合器提供足够的输入/输出控制线接入，目前基于该技术已经实现百比特数目量级的超导量子处理器。

(4)实现量子芯片三维立体封装的硅通孔技术。在半导体工艺中，硅通孔技术是实现芯片之间互连最新的先进封装技术。它可以在芯片和芯片之间、晶圆和晶圆之间实现垂直电气互连[78，79]，具有减小电路连接长度、信号延迟、寄生电容/电感，实现芯片间的低功耗、高速通讯和实现器件集成小型化等优点。最近几年，各个研究团队试图通过硅通孔技术实现超导量子比特芯片中三维立体集成，以支持高密度的量子比特系统。如图6(d)所示，在2020年的一项工作中[80]，麻省理工学院的研究团队就展示了具有高深宽比的硅通孔，同时结合倒装焊技术和多层走线技术，实现了超导量子比特的集成封装，并对量子比特进行高保真读出，验证了直接在硅通孔集成芯片表面上制备量子比特而不会影响其性能的可行性。随着超导量子电路的结构变得复杂，通过硅通孔技术和其他先进封装工艺实现超导量子比特之间的互连，有望解决大数目量子比特芯片的集成化问题。

近几年来，各个研究团队结合对超导比特结构的合理优化，将先进的半导体加工技术应用在超导量子比特的集成化中，量子芯片已经达到上百个比特数目量级。但是如何优化超导量子比特的空间结构和减少控制线使用，实现量子比特的小型化和芯片之间的量子互连，依然是目前超导量子比特面向大规模集成的挑战之一。

07超导量子比特信号放大

超导量子比特的量子态测量信号是在极端低温环境(接近于绝对零度)下单光子量级的弱信号。该弱信号需要放大超过100 dB(即100亿倍)，才可以在室温时采集到信号进行数据分析。在整个信号放大的链路中，前级放大器引入的噪声会被后面级联的放大器放大，因此第一级的放大器性能至关重要。商用的半导体低噪声微波放大器由于其耗散性质而无法达到系统量子噪声水平。于是，人们发展了量子极限参量放大器作为量子比特测量的第一级放大，以实现信噪比好的信号探测。

参量放大器伴随着通信技术的发展由来已久[81—84]。约瑟夫森效应在实验上被验证后，研究人员根据约瑟夫森结这一“非线性电感”的周期性调控，实现参量放大[85]。随后研究人员又对这一参量放大器的带宽、噪声以及频段等进行深入研究[86，87]，在20世纪八九十年代就可以达到近量子极限噪声水平[88—91]。不过由于约瑟夫森结本身应用场景的特殊性，这种参量放大器在后来的一段时间内并没有受到广泛的关注。进入21世纪后，由于超导量子计算的飞速发展，人们又重新审视超导参量放大器在量子比特测控中的作用[92—96]，并利用约瑟夫森结便于加工设计的特点，直接制备如图7(a)所示的适合于量子态测量、可以达到量子极限的参量放大器样品[97]。特别是在2011年，加州大学伯克利分校的研究人员利用该放大器在超导量子比特的色散测量中，观测到transmon比特的量子跳跃现象[98]，预示着参量放大器在接近绝对零度的单光子量级弱信号探测中具有独特的优势。

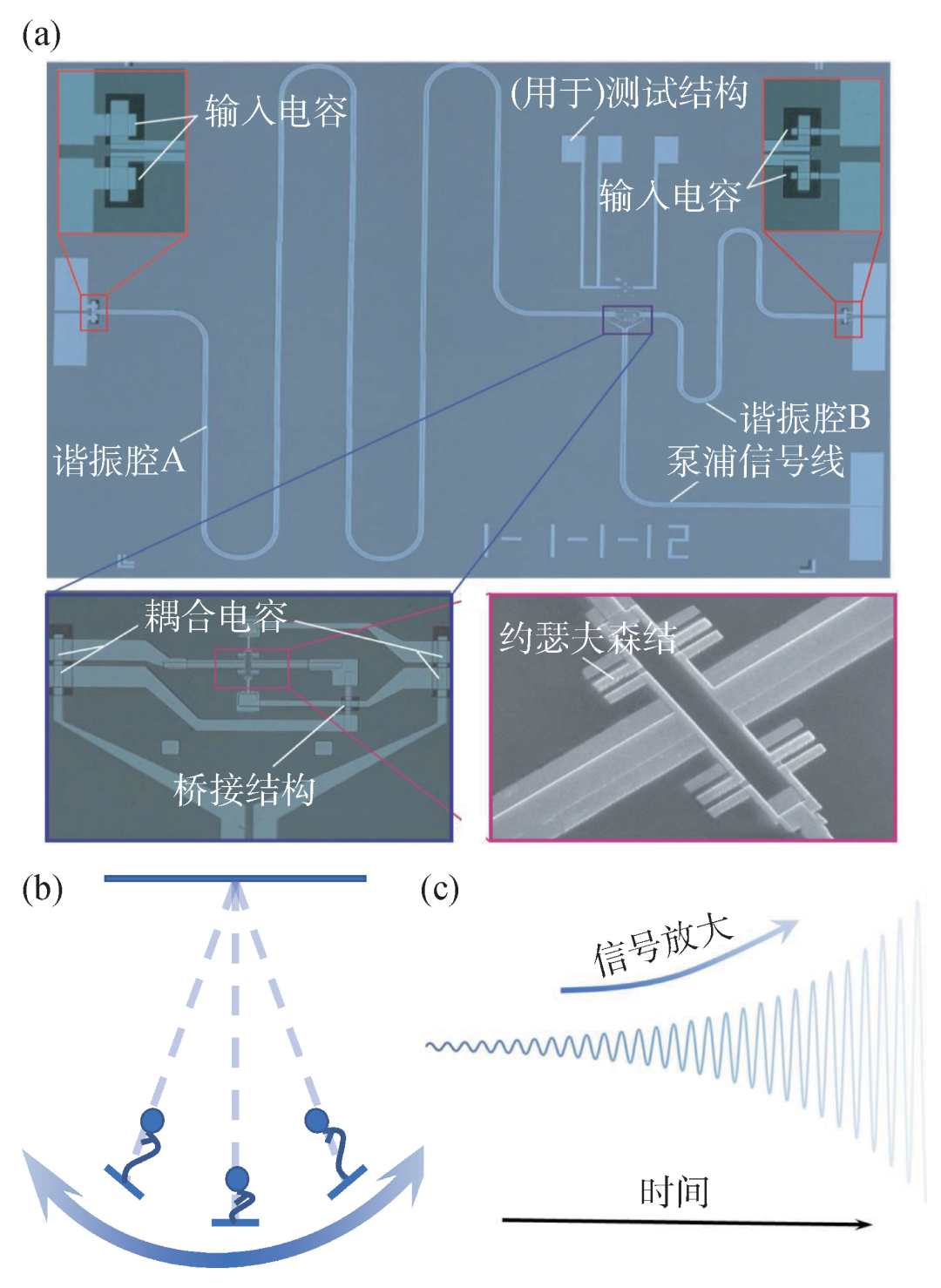
图7 (a)与谐振模式共振类型的参量放大器样品图[97]。其中，左上小图和右上小图是样品和外部信号的耦合结构，该结构使用电容耦合。左下图是泵浦线与两个谐振腔耦合结构的放大图，包括泵浦线与两个谐振腔之间的耦合电容以及谐振腔A结构跨过谐振腔B的桥接结构，右下图是左下图中为整个芯片样品提供非线性项的约瑟夫森结结构的放大图;(b)参量放大器的荡秋千模型;(c)在合适的参量控制下，信号强度将随着时间变长而越来越大

参量放大器是将一个特定参数的大功率泵浦信号和待测弱信号一起输入，泵浦信号会转化为弱信号和一些其他信号，最终实现弱信号的增强。这个原理可以简单的以如图7(b)中荡秋千模型来类比，如果人在秋千摆动的最高点站立起来，逐渐地随着秋千到达最低点蹲下，通过有规律的随着秋千摆动，实现将自身的摆动(调控的参量)转换成秋千的高度(放大的信号)。如果按照单摆模型去建模会发现，之所以会发生这种转换是由秋千的运动存在非线性项导致。并且在一定的条件下，按照这样的规律荡秋千的时间越长，如图7(c)所示，秋千所能达到的高度将越高。

超导薄膜材料的动态电感，或是约瑟夫森结的等效电感，都具有非线性特征，可以用来实现超导参量放大器。此外，想要实现一个可观的信号增益，在参量调控的同时还需要待测信号在非线性器件中停留足够长的作用时间。因此，可以将参量放大器分为两类。

(1)基于与谐振模式共振的参量放大器。具有代表性的是将约瑟夫森结和某一谐振腔组合形成有一定品质因子(Q值)的谐振模式的参量放大器。越高的Q值将使待测信号在模式内停留时间越长，以实现足够高的增益。显然，这种参量放大器的增益和带宽是相互限制的：因为Q∼1/γ，即信号停留时间长，模式的Q值要高，那么能够停留时间长的光子频率带宽γ就窄。所以一开始这种放大器都是窄带参量放大器[99，100]，只能用于对某一超导量子比特态读取信号的放大。为了能够实现多个量子比特读取腔信号的同时放大，后来又发展了如图8(a)中通过阻抗匹配实现宽带的放大器[101，102]。

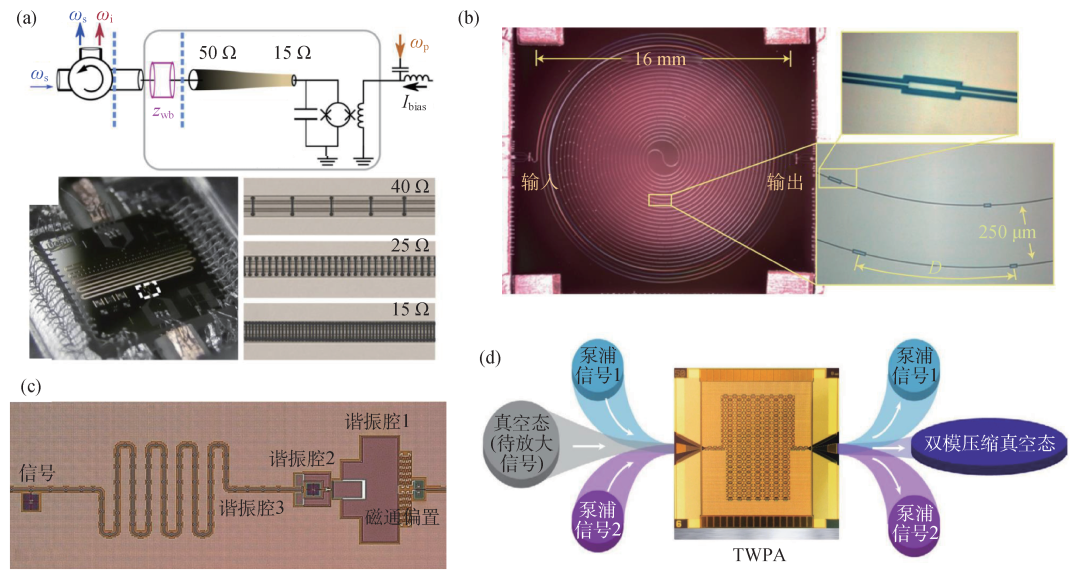
图8 几种具有高增益、高带宽和高饱和功率的参量放大器 (a)基于阻抗匹配实现的共振类型参量放大器结构图[101]。放大过程通常是：左端弱信号输入(ωs)，经过阻抗连续变换，然后到达有约瑟夫森结的谐振器，此时从右侧加入合适的直流偏置和泵浦信号(ωp)。最终弱信号反射回去的信号经过循环器(最左边的结构)分离出去，变为频率仍为弱信号的已经实现放大的信号，以及一个不需要的闲置信号ωi。左下图为参量放大器整个芯片图，右侧为阻抗变换结果样品图;(b)基于超导薄膜材料动态电感实现的行波参量放大器样品图[104]。其中，左侧图为行波参量放大器的整体结构尺寸示意图，右下图是行波参量放大器中在不同的空间位置处设计如右上图中的阻抗结构，以实现相应的非线性电感;(c)基于切比雪夫型阻抗匹配网络实现的参量放大器样品图[110];(d)利用约瑟夫森结阵列的行波参量放大器实现压缩真空态示意图[108]

(2)基于长距离非线性介质的参量放大器。该类放大器通常是行波型的参量放大器(TWPA)，它需要制备一个足够长距离的非线性介质，使得待测信号经过时间长，以实现可观的增益。TWPA的理论提出可以追溯到20世纪80年代[103]，不过由于空间上长距离的非线性介质对材料性质、阻抗匹配等要求苛刻，样品加工上十分具有挑战性。直到2012年，通过使用超导薄膜材料NbTiN实现高阻抗的动态电感，基于动态电感的非线性实现了如图8(b)所示的TWPA[104]。NbTiN的超导临界电流大，TWPA可以达到大于−70 dBm的饱和功率。另外根据2013年提出的理论方案[105]，直接用上千个约瑟夫森结串联实现足够长距离的非线性介质，也可以实现达到量子极限噪声的参量放大器[106，107]，并且还可以实现如图8(d)中具有宽带宽的双模压缩真空态[108]。TWPA这些特征意味着它在超导量子比特多通道同时测量方面具有潜在的优势。

相对于普通参量放大器，超导参量放大器的一大优势是利用超导体无耗散的特点，噪声可以达到量子极限。但是通常由于样品材料本身的介电损耗，或是基于约瑟夫森结非线性产生的模式色散效应，都会影响放大器增益。值得注意的是，最近谷歌的量子研究团队通过引入微波工程中的阻抗匹配技术，实现切比雪夫型带通阻抗匹配网络[109]，实现了图8(c)中的高饱和功率、高带宽、高增益的参量放大器[110]。量子极限参量放大器不仅在超导量子比特态读取中至关重要，同时它还有其他方面的应用，如量子压缩态制备[89，111]、宇宙暗物质探测[112—114]等等。

08展 望

量子计算具备随硬件规模指数增长的运算能力，它可以完成一些传统计算机不能够有效完成的计算任务。历经二十多年的研究，超导量子计算逐渐脱颖而出成为最有前景实现通用量子计算机的方案之一。目前以IBM和谷歌为代表的研究团队提出以量子为中心的超级计算机架构，预计在不久的将来会实现大规模超导量子比特的集成化。

超导量子比特结构是否是量子计算中的“量子晶体管”还有待产业发展的验证。但是值得肯定的是，基于约瑟夫森结的超导量子器件已经初具量子生态产业链雏形，其中包括低温器件研究、弱信号精密测量、多体强关联量子系统模拟以及量子增强的人工智能等等方向都正在蓬勃发展中，甚至在发展超导量子比特集成化工艺技术的同时，也可能启发“后摩尔时代”新型半导体晶体管的研究。

现在人们普遍相信量子计算有可能成为未来科技加速演进的催化剂，一旦取得突破，将在基础科研、新型材料与医药研发、信息安全和人工智能等诸多领域产生颠覆性影响，其发展与应用对国家科技发展和产业转型升级具有重要的促进作用。基于超导量子器件的量子信息技术已经成为信息通信技术演进和产业升级的关注焦点之一，在未来国家科技发展、新兴产业培育、国防和经济建设等领域，将产生基础性乃至颠覆性重大影响。

审核编辑：汤梓红