上节我们从公式角度分析了自由空间和周期排布空间的电子的存在概率问题,那么这节我将会通过棋盘的例子帮助大家定性理解两者之间的区别。
棋盘实验
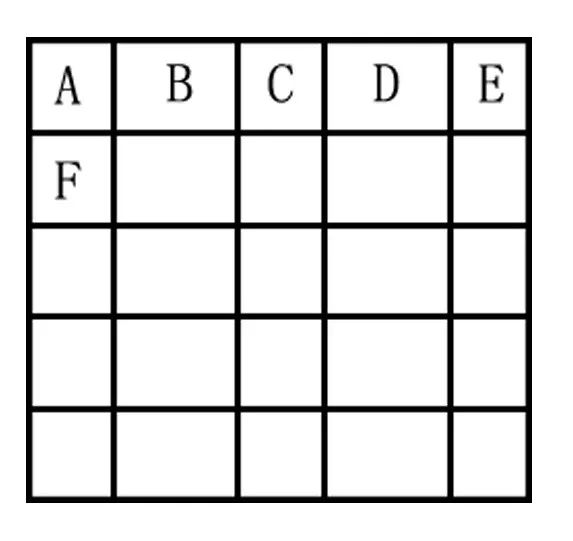
想象两张棋盘,其中一张没有格线,另一张周期性布满格线,如下图所示。

将电子想象为一颗棋子。这颗棋子在没有格线约束的情况下,可以任意放在棋盘上的任何一个位置,也就是说这颗棋子出现在棋盘上任何位置上的概率相同。
而如果将这颗棋子放入布满周期性格线的棋盘上,那么 这颗棋子在每个格子出现的概率是周期性重复的,重复的周期与格线的周期相同。 如上图右侧所示,我们假设将整个棋盘等分为5*5的格子,那么棋子在每个格子出现的概率为1/25,重复周期是1格。
如果棋盘没有被等分,如下图所示,我们假设棋子在A位置出现的概率为a,B位置的概率为b,那么ABCDE的概率分别为ababa,F之后的第二行的概率为ababa,我们发现 这颗棋子在每个格子出现的概率是周期性重复的 ,重复周期为5格。
但是若选定某个格子,那么在这个格子内部的分布则受格线的边界条件所限制。
首先格线及附近一定距离是不能摆放棋子的,这就相当于禁止电子存在的能级;其次,格子内部不同位置的棋子出现概率,又与格子的尺寸等相关,所以在单个格子内电子出现概率并非处处相同。
这里描述的每一个格子其实就相当于一个能级,而所有格子合起来就组成能带,所有格线组合起来就组成禁带。而格子所处的位置不同,棋子放入其中所需的能量也就不同,所以概率相同,但能量不同,即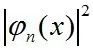 相同,但k
相同,但kn所对应的En不同。(注:为更好地解释自由/周期空间电子出现的概率问题,我们列举了棋盘实验,但实际情况下的能量-概率关系与棋盘实验所得出的结论有所不同)
费米分布
显然任何电子的能量都是有限的,因此,有限的能级会被电子所占据,那么电子在不同能级的分布概率如何呢?这里就需要引入半导体中非常重要的一个分布函数叫做费米-狄拉克分布函数,通常简称为费米分布,即:
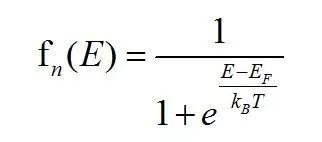

因此, 费米能级以下的能级被电子占有的概率远远大于费米能级以上的能级。 (扩展:随着温度的上升,这个变化趋势会变缓,也就是电子占有费米能级以上能级的概率就会增加。)
电子的自激发和空穴的产生

根据泡利不相容原理,对于已经被电子占满的能带就不能再有其他电子加入,因此不能导电;反之对于没有被电子占满的能带则还可以有其他电子加入,因此可以导电。
半导体中将费米能级以下的能带称为价带,费米能级以上的能带称为导带。
显然,虽然概率很低,但导带底部存在一定被电子占据的概率,这就是半导体中自发产生自由电子的机制,称为自激发。
自激发进入导带的电子,因为能带中的绝大多数能级没有电子,因此电子可以自由移动。而且随着温度的升高,自发产生自由电子的概率也会升高。

此外,根据电中性原理,价带和导带的电子分布具有对称性,也就是说,导带中增加多少电子,价带中就相应地应该减少多少电子,物理概念上通常将这个过程描述为:由于温度的原因,价带的电子自发 “激发” 到了导带。
由于价带中电子数量远远大于激发到导带中的电子,如果价带中的电子状态也以每个电子为描述对象,那么过程会非常复杂。
考虑导带和价带的对称性, 把价带中因为电子激发而留下的空余能级想象为另一种电荷,取名叫做“空穴”。 因此,电子和空穴总是成对的产生,好比阳光下一个物体和他的影子,不可能独立产生。
至此,我们介绍完毕电荷自发产生的过程,下一节我将为小伙伴们讲述自发产生的电荷浓度问题。
文末总结
1、通过棋盘实验理解能级、禁带、能带;

3、通过实际来分析费米分布,理解价带和导带:半导体中将费米能级以下的能带称为价带(不能导电),费米能级以上的能带称为导带(能导电)。
4、得到电子/空穴产生的原因:由于导带底部存在一定被电子占据的概率,半导体中会自发产生自由电子,该机制被称为自激发。考虑导带和价带的对称性,把价带中因为电子激发而留下的空余能级想象为另一种电荷,取名叫做“空穴”。
-
半导体
+关注
关注
335文章
27984浏览量
225319 -
电荷
+关注
关注
1文章
643浏览量
36349
发布评论请先 登录
相关推荐
TXB0104与TXS0102两者之间有什么区别吗?
请问TMS320F2802PZA和TMS320F2802PZA-60两者之间的区别
单片机和嵌入式两者有什么区别和联系呢
怎样去区分RK3288和RK3288W两者之间的型号呢
有人可以告诉我keil和stm32cube ide两者之间有什么区别吗
建立自由空间光学系统
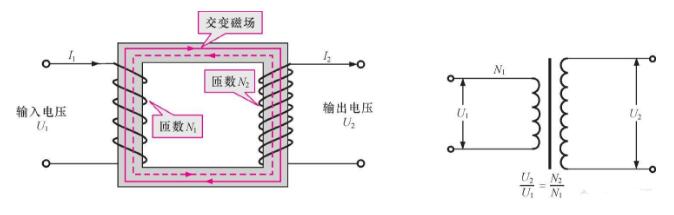
读懂变压器空载与负载及两者之间的区别




 自由空间和周期排布空间的电子两者之间的区别
自由空间和周期排布空间的电子两者之间的区别










评论