前文讲了电子在不同能量下的分布概率,显然概率随能量是遵守费米分布规律连续性变化的。
至于电子在某个能量状态下是否能够存在,得看 是否存在对应于这个能量值的能级,并不是有出现概率就一定存在 。
回忆之前所举的棋盘格子的例子,一个格子代表一个能级,一个能级对应一个能量。对于电子来说,一个能量可以存在两个状态,即两个不同旋转方向,也就是说,若将一个电子比喻成一个棋子,那么一个格子中能放两个不同旋转方向的电子。

那么要想知道电荷的浓度,相当于想要知道单位面积内的格子里有多少个电子。接下来我们将分别通过公式推导和定性的方式来解释自发产生的电荷浓度。
电荷浓度的公式推导
01
在已知电子存在于每个格子的概率的情况下,只需要知道棋盘单位面积内总共有多少个格子即可,即用单位面积内的格子数乘以每个格子中电子的分布概率就得到总的电子数量。
上述单位面积的棋盘和格子的关系,对应到En-kn关系中,就是单位能量中的波矢数量,即dE中对应的kn数量,物理上称为(能)态密度,即单位能量范围内可存在的状态密度。
显然,对于导带,态密度可表达为N c (E)=dX/dE,其中,dX表示在能量dE范围内的能态数量。
导带中电子的能量表达式为
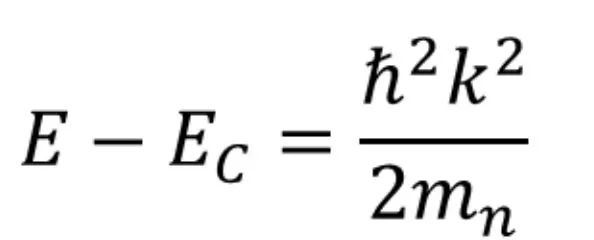

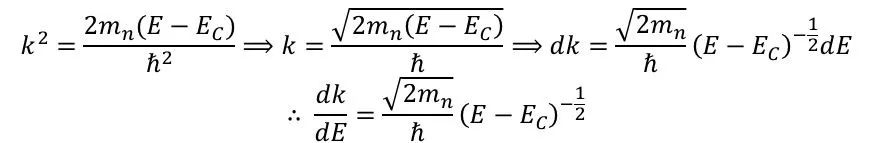
欲求得态密度dX/dE,在知道dk/dE的情况下,将其做一个变形
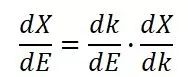

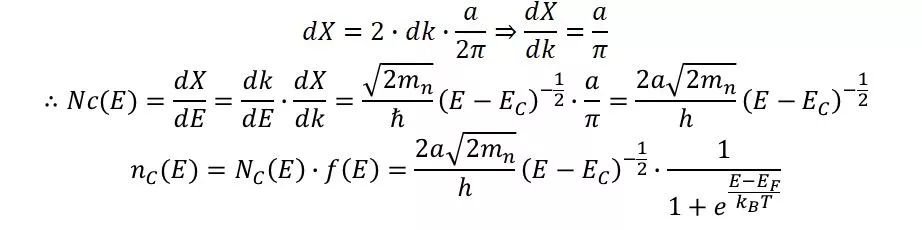
因为
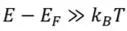 ,所以上式可以近似得到导带中电子浓度为
,所以上式可以近似得到导带中电子浓度为
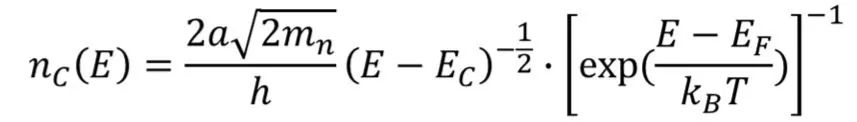
同理,可以推导出价带中的空穴浓度,但要注意的是
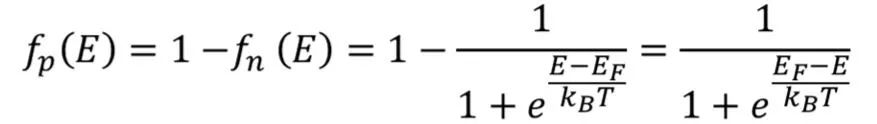
这两个表达式即描述了在温度T,导带和价带中对应某个能量本征激发的电荷浓度。
电荷浓度的定性解释
02
电荷浓度的推导涉及到固体物理的基础知识,尽管前文以棋盘为例进行类比,但要理解还是不大直观,其原因主要在于E-k(能量-波矢)空间比较抽象,即倒格子空间,这是分析微观粒子量子化特性的一个基本空间,完全是一个想象出来的数学抽象空间。
为什么需要这么一个抽象空间呢?因为微观粒子的描述方式有一个基本方程式叫做薛定谔方程,描述了 微观粒子的波函数和能量之间的关系,波函数表征的则是粒子出现的概率 。
如前文提到空间自由电子的波函数表达式为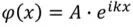
 ,k是描述波函数的重要物理量,所以在E-k所描绘的空间中,可以比较方便地推导各种微观粒子的状态。
,k是描述波函数的重要物理量,所以在E-k所描绘的空间中,可以比较方便地推导各种微观粒子的状态。
至于薛定谔方程的由来,以及如何通过薛定谔方程推导某种具体粒子的状态,在此不做赘述。
还是结合棋盘的例子,这里再进一步做解释,大致逻辑可以梳理如下:若将一个电子比作一枚棋子,能级比作一个棋盘上的格子,能带比作一层又一层的棋盘。棋子有一个特性就是一直处于旋转状态,可以顺时针旋转,也可以逆时针旋转,犹如围棋中有白棋和黑棋。
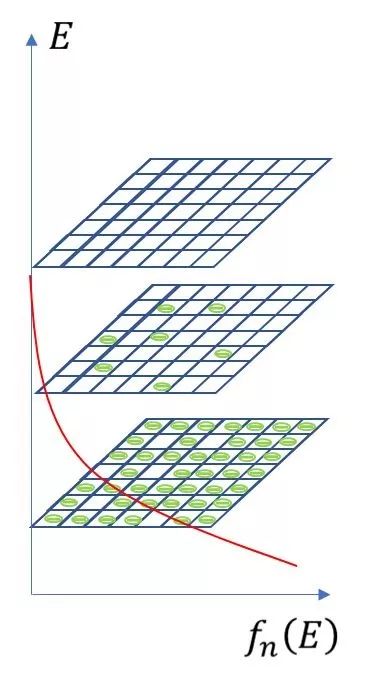
一个格子只能放一颗白棋或者一颗黑棋或者一颗白棋加上一颗黑棋,也就是说 一个能级最多只能存在两个不同旋转方向的电子 ,原则上棋子可以在空间中任何位置出现,包括棋盘之上以及棋盘之间的空间,其出现的规律符合费米分布。
但是只有将棋子放到棋盘之上的格子之中,才符合下棋的规则,所以并不是有出现概率就一定会出现,放入哪一层的棋盘以及棋盘中哪一个格子的概率同样遵从费米分布,显然某一层棋盘中能放入多少棋子(电子浓度),就看 这个棋盘中有多少格子,以及棋子放入这些格子的概率 。格子的数量和周期则与材料本身的特性相关,如原子之间的间距、质量等。
文末总结
1、通过公式推导,得出导带中电子浓度:
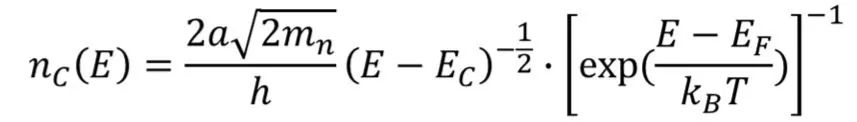
2、同理得到价带中的空穴浓度:
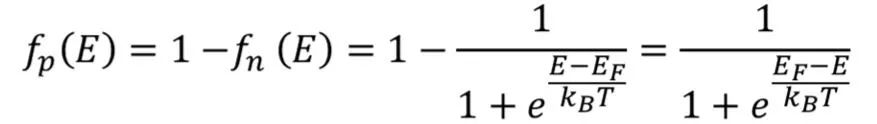
3、定性解释:
以棋盘实验为例,原则上棋子可以在空间中任何位置出现,但是只有将棋子放到棋盘之上的格子之中,才符合下棋的规则,所以并不是有出现概率就一定会出现,某一层棋盘中能放入多少棋子(电子浓度),就看这个棋盘中有多少格子,以及棋子放入这些格子的概率。
-
电荷
+关注
关注
1文章
643浏览量
36336
发布评论请先 登录
相关推荐
电荷泵供应多少电流?
[专]电荷为何自发产生——第一弹
[专]电荷为何自发产生——第二弹
你真的懂Word吗
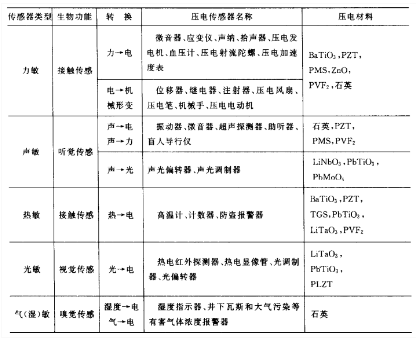
压电陶瓷传感器的特性及工作原理解析
移动的电荷如何产生磁场
双视图几何:你真的理解吗?
自发辐射的机制是什么?为什么会自发辐射?




 你真的理解自发产生的电荷浓度吗?
你真的理解自发产生的电荷浓度吗?










评论