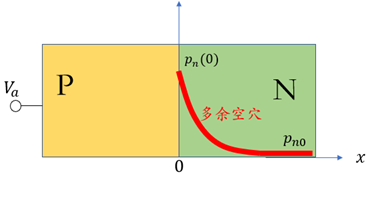
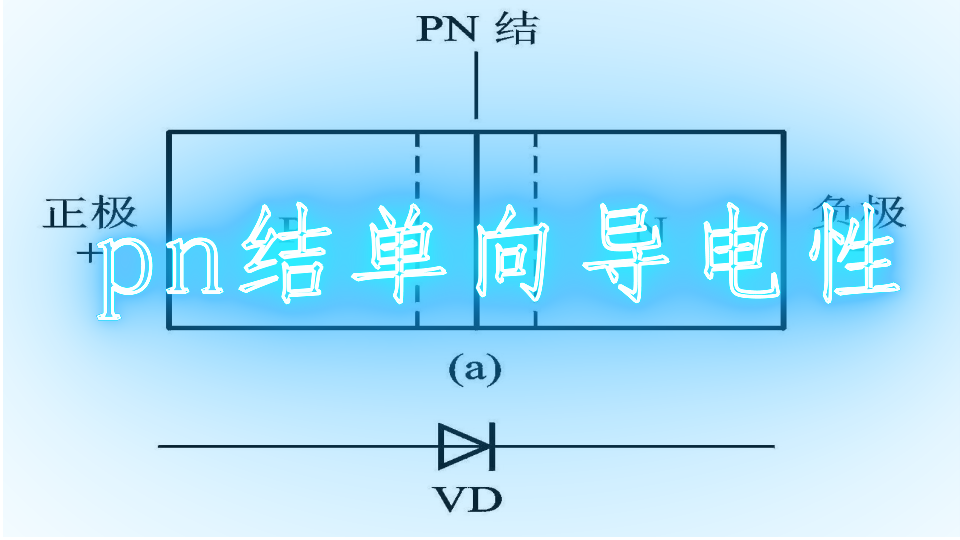
下面简要推导PN结导通状态下的电荷浓度分布以及电流、电压的关系。如下图:
当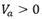 ,那么克服内建电势而施加在PN结两个电极之间的电势差为
,那么克服内建电势而施加在PN结两个电极之间的电势差为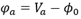 。空穴从P区注入N区,除部分被N区多子复合外,还余下部分“多余空穴”;电子情况类似。分析PN结导通状况,关键就是分析这些多余载流子的分布情况。这里讨论两种状态:
。空穴从P区注入N区,除部分被N区多子复合外,还余下部分“多余空穴”;电子情况类似。分析PN结导通状况,关键就是分析这些多余载流子的分布情况。这里讨论两种状态:
1)平衡状态,即PN中没有电流通过,

2)稳定状态,即虽然有电流通过,但是电荷浓度不随时间变化。(显然平衡状态是稳定状态的一种特殊状态。)
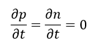
对于平衡状态,扩散电流与漂移电流之和为0,以空穴为例,
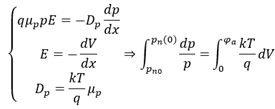
化简后得到,

其中,
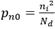
同理,对于平衡态下P区的电子浓度,

其中,
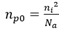
因此,当多余载流子被注入P区或者N区后,其浓度分布随电势 呈
呈 指数衰减趋势,直到等于平衡态下的热激发浓度。
指数衰减趋势,直到等于平衡态下的热激发浓度。
对于稳定状态,还是以空穴为例。稳定状态下,PN半导体应处于电中性状态,所以电场 。回顾关于电荷变化的讨论,影响电荷变化的因素有四个,及扩散电流、漂移电流、产生电流、复合电流。在杂质掺杂的半导体中施加正向电压,自发产生的电流几乎可以忽略。因此只有考虑扩散电流和复合电流。
。回顾关于电荷变化的讨论,影响电荷变化的因素有四个,及扩散电流、漂移电流、产生电流、复合电流。在杂质掺杂的半导体中施加正向电压,自发产生的电流几乎可以忽略。因此只有考虑扩散电流和复合电流。
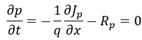
其中,  ,
,  所以要想得到
所以要想得到 随
随 的变化趋势,就必须先知道
的变化趋势,就必须先知道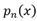 的分布。将
的分布。将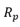 和
和 带入上式,可以得到,
带入上式,可以得到,
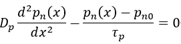
求解该方程可得到,

其中,

平衡状态是稳定状态的一个特殊状态,因此将平衡状态作为边界条件,将平衡状态的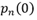 带入,
带入,
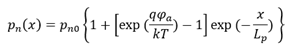
由此,可以计算得出任意 位置的空穴电流。这里计算
位置的空穴电流。这里计算 位置的空穴电流,
位置的空穴电流,

同理,计算 位置的电子电流,
位置的电子电流,

电路回路中电流处处相等,所以将 处的空穴电流与电子电流相加即可得到总的电流,
处的空穴电流与电子电流相加即可得到总的电流,
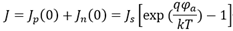
其中,

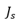 被称为PN二极管的饱和电流。
被称为PN二极管的饱和电流。
【延伸】当 ,即PN结反向承压时,上面推导过程依然成立,相应计算得到的电流即为反向漏电流。但需要注意的是,反向承压时的本征激发(
,即PN结反向承压时,上面推导过程依然成立,相应计算得到的电流即为反向漏电流。但需要注意的是,反向承压时的本征激发(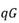 )漏电流就不能被忽略了。
)漏电流就不能被忽略了。
举例:以Si-IGBT为例,假设P型掺杂浓度为 ,N型掺杂浓度为
,N型掺杂浓度为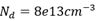 。本征掺杂浓度为ni=3.87e16T^1.5exp(-7.02e3/T);空穴迁移率为up=495*(T/300)^(-2.2)
。本征掺杂浓度为ni=3.87e16T^1.5exp(-7.02e3/T);空穴迁移率为up=495*(T/300)^(-2.2)
如下图:
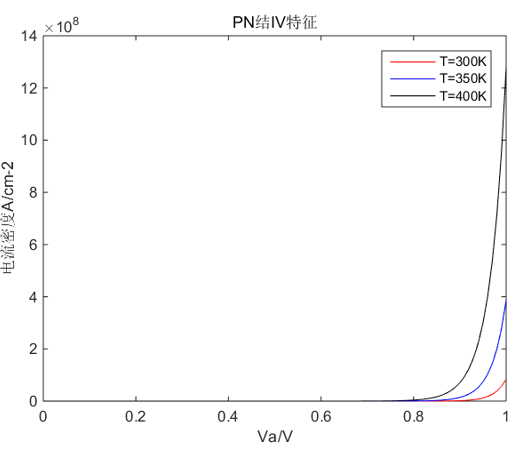
可以看出,随着温度的升高,相同外加电压的情况下,PN导通电流迅速上升。
-
二极管
+关注
关注
148文章
9816浏览量
168025 -
半导体
+关注
关注
335文章
27885浏览量
224315 -
IGBT
+关注
关注
1269文章
3855浏览量
250536 -
PN结
+关注
关注
8文章
486浏览量
49014 -
电流电压
+关注
关注
0文章
205浏览量
11956
发布评论请先 登录
相关推荐




 说说IGBT中PN结的导通状态
说说IGBT中PN结的导通状态











评论