上一节我们讨论了栅极与半导体材料之间的功函数差,本节我们讨论绝缘层电荷的影响。
绝缘层相当于一个电容,分析施加其上的电压,就必须先分析清楚绝缘层两侧及内部的电荷分布。
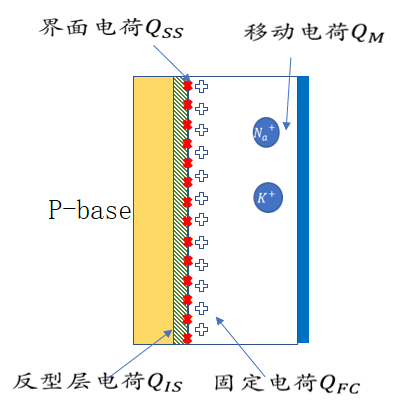
从半导体到栅极,绝缘层内外存在四种电荷(这里均为面电荷密度),
1.反型层电荷 (Inversion Charge),来自半导体表面的反型层,宽度一般大约10nm量级,紧邻绝缘层表面;
(Inversion Charge),来自半导体表面的反型层,宽度一般大约10nm量级,紧邻绝缘层表面;
2.界面态电荷 (Interface Charge),来自半导体与绝缘层界面的悬挂键、不饱和化学键等,会在半导体禁带中产生缺陷能级,通常带正电(工艺中通常通过氢环境退火来修复);
(Interface Charge),来自半导体与绝缘层界面的悬挂键、不饱和化学键等,会在半导体禁带中产生缺陷能级,通常带正电(工艺中通常通过氢环境退火来修复);
3.固定电荷 (Fixed Charge),以二氧化硅来说,通常来自于生长过程中氧的缺失造成的空位,在氧化硅生长之初易出现,所以通常在纳米尺度的范围内,同样带正电;
(Fixed Charge),以二氧化硅来说,通常来自于生长过程中氧的缺失造成的空位,在氧化硅生长之初易出现,所以通常在纳米尺度的范围内,同样带正电;
4.可移动离子电荷 (Mobile Ionic Charge),与生产工艺环境的洁净度有关系,一般为钠离子或者钾离子等,带正电。
(Mobile Ionic Charge),与生产工艺环境的洁净度有关系,一般为钠离子或者钾离子等,带正电。
除反型层电荷 之外,其他电荷基本来自于工艺环境和材料性质等客观因素,应在制备过程中尽量优化,下面粗略分析维持
之外,其他电荷基本来自于工艺环境和材料性质等客观因素,应在制备过程中尽量优化,下面粗略分析维持 多大的电压,该电压即为在此反型状态下的阈值电压。
多大的电压,该电压即为在此反型状态下的阈值电压。
因为推导过程较为繁琐,这里只梳理分析的逻辑,见右图,感兴趣的可以试着推导一下:
1.根据高斯定理,维持 需要相应的电场;
需要相应的电场;
2.根据泊松方程,电场求解需要知道电势分布,电势分布需要知道电荷浓度分布;
3.电荷浓度分布与形成反型层的电势差 相关。
相关。
这里给出实现“强反型”的结论:


因为没有详细推导,这里漏掉了关于“强反型”的定义,做个补充说明:一般情况下,只要能带弯曲使得费米能级越过本征能级,即实现了反型,这种情况被称为“弱反型”,表现为 并不会随着
并不会随着 的增长而快速增长;当费米能级越过本征能级一倍,即图中
的增长而快速增长;当费米能级越过本征能级一倍,即图中 时,
时, 将随
将随 呈指数级增长,这种情况被称为“强反型”。
呈指数级增长,这种情况被称为“强反型”。
综上,得到与氧化硅相关的电荷分布,电荷除以电容,即得到维持这些电荷所需要的电压;再加上前面所分析的栅极与半导体之间的功函数差,以及“强反型”的能带弯曲 ,即可得到阈值电压的表达式。
,即可得到阈值电压的表达式。
假设氧化硅的厚度为 ,那么可定义其单位电容为:
,那么可定义其单位电容为:

那么阈值电压可表达为(金属作为栅极):

阈值电压可表达为(N型多晶硅作为栅极):

其中 ,
,
阈值电压表达式右边第一项为栅极与半导体之间的功函数差,第二项为“强反型”的能带弯曲 ,第三项为维持强反型
,第三项为维持强反型 ,氧化硅电容需要施加的电压,第四项为氧化硅电容表面及体内固有电荷充电形成的电压。
,氧化硅电容需要施加的电压,第四项为氧化硅电容表面及体内固有电荷充电形成的电压。
举个例子,对于P型硅,掺杂浓度为Na=5e17cm-3,均匀掺杂;栅极为N型多晶硅,掺杂浓度为Npoly=1e20cm-3,栅氧厚度为d=120nm。
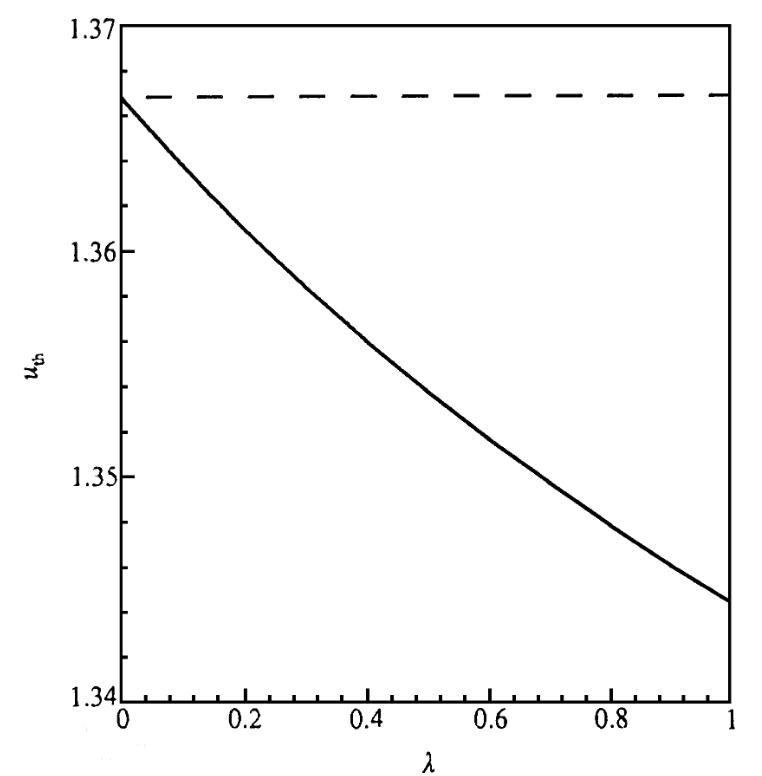
硅的本征浓度为1.45e10cm-3,相对介电常数为11.5;不考虑工艺引入的缺陷或者移动电荷,计算得到 我们看看Na、d以及栅氧电荷(以Qss为例)对阈值电压的影响。
我们看看Na、d以及栅氧电荷(以Qss为例)对阈值电压的影响。

-
多晶硅
+关注
关注
3文章
243浏览量
29399 -
半导体
+关注
关注
335文章
27826浏览量
223839 -
IGBT
+关注
关注
1269文章
3846浏览量
250369 -
电容电压
+关注
关注
0文章
74浏览量
11283 -
阈值电压
+关注
关注
0文章
73浏览量
51538
发布评论请先 登录
相关推荐
解答74HC14中正向阈值电压和负向阈值电压是什么/电压为多少
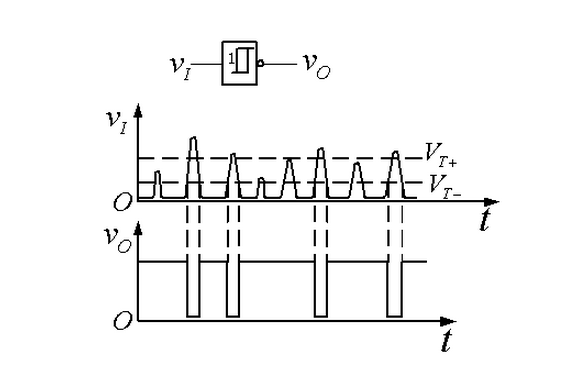
MOS管阈值电压的问题
MOS管阈值电压与沟长和沟宽的关系
不同Vt cell工艺是怎么实现的?阈值电压和哪些因素有关系?
影响MOSFET阈值电压的因素
什么是MOS管亚阈值电压?MOSFET中的阈值电压是如何产生的?
浅谈影响MOSFET阈值电压的因素
MOSFET阈值电压是什么?影响MOSFET阈值电压的因素有哪些?
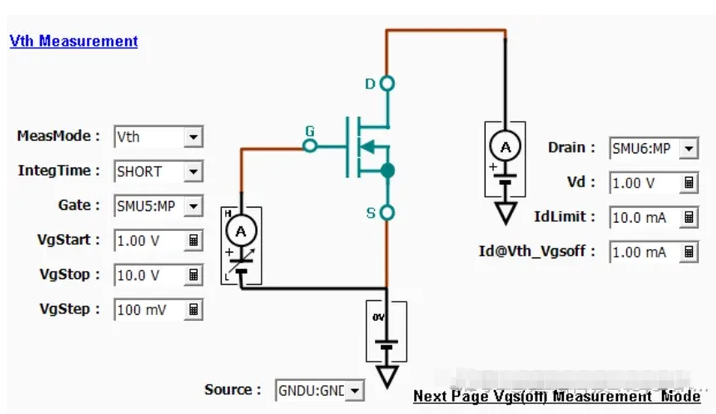




 IGBT中的MOS结构—阈值电压(下)
IGBT中的MOS结构—阈值电压(下)
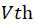
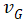











评论