当我们已知一个系统的闭环传递函数时候,我们通常有两种方法来判断系统的稳定性。第一种是时域分析方法,可以观察闭环传递函数的阶跃响应;第二种是频域分析法,可以观察闭环传递函数的频率响应。频域分析方法中,伯德图一般被广泛使用。这两种分析方法都可以借助Matlab工具得到直观的曲线,非常有助于我们对问题的分析。
Note1:时域分析时,除了常用的阶跃信号作为输入激励外,还常使用脉冲信号和斜坡信号作为激励。Note2:频域分析法,我们既可以选择环路增益的伯德图,也可以选择闭环传递函数的伯德图。
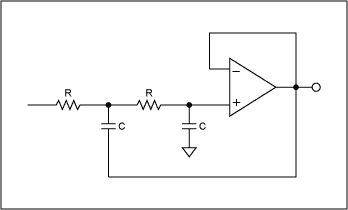
以一个非常有代表性的标准二阶系统为例,可以通过Matlab研究该系统的特性。其闭环传递函数如下(公号不支持公式编辑也真是个亮点,直接上图吧):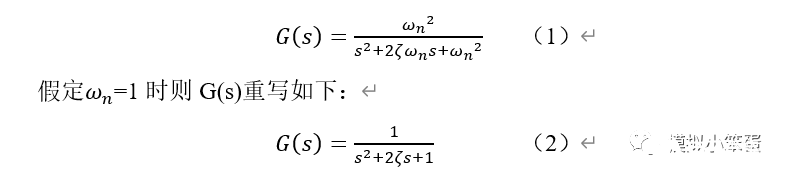 下面针对公式2进行分析。01 时域
下面针对公式2进行分析。01 时域
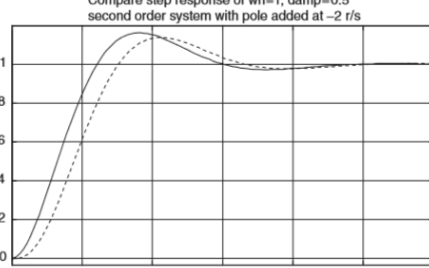
当ζ取不同的值时,该系统的阶跃响应会是怎样的呢?设计如下所示的Matlab代码。仿真波形如图1所示,三维波形如图2所示。
% G(s)=ωn^2/(s^2+2ζωn s+ωn^2 ).whenωn=1,research unit-step response
% with different ζvalues.
%------------------------------------------------------------------------
t=0:0.2:10;
zt=[0.1 0.2 0.4 0.6 0.8 1.0];
for n=1:6
num=[1];
den=[1 2*zt(n) 1];
[y(1:51,n),x,t]=step(num,den,t);
[y(1:51,n),x,t]=impulse(num,den,t);
end
plot(t,y)
grid
title(‘plot of unit_step response curves with omega_n=1 and zeta=0.1,0.2,0.4,0.6.0.8,1.0’)
xlabel(‘t secs’)
ylabel(‘response’)
text(3.7,1.7,‘zeta=0.1’)
text(3.5,0.8,‘zeta=1.0’)
% to plot a three-dimensional diagram,enter the command mesh(t,zeta,y‘)
figure(2)
mesh(t,zt,y’)
title(‘three-dimensional plot of unit-step response curves’)
xlabel(‘t secs’)
ylabel(‘zeta’)
zlabel(‘response’)
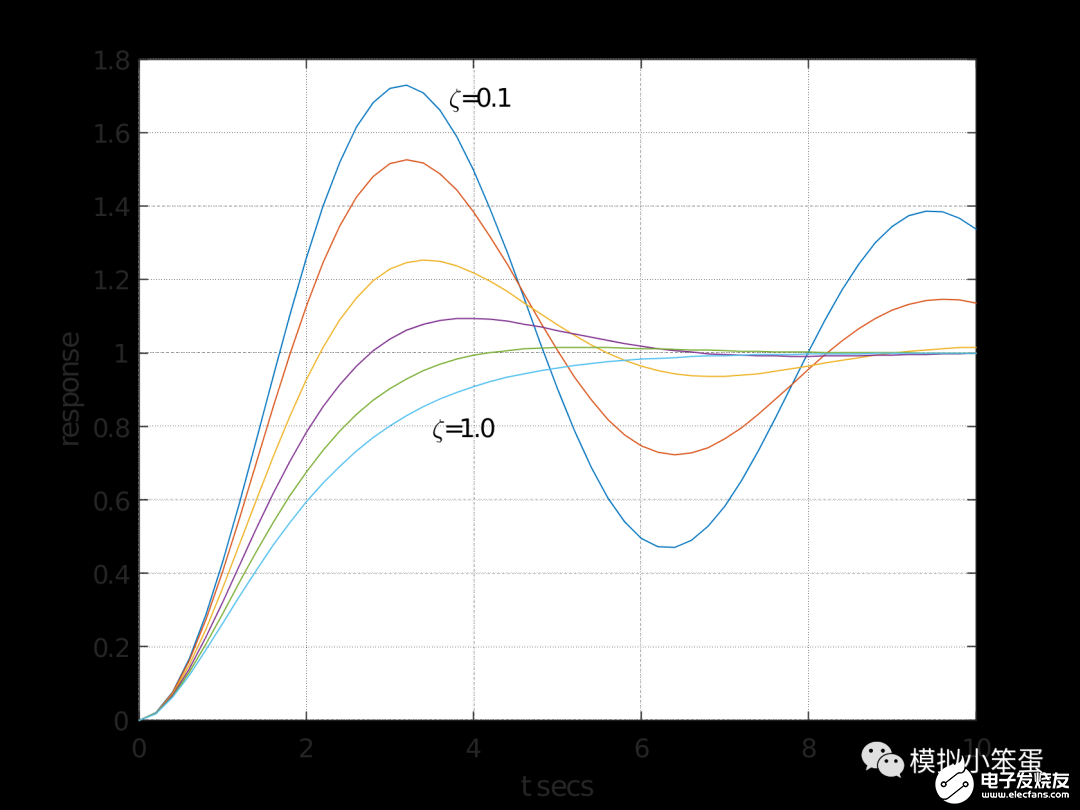
图 1 ζ取不同值时的闭环阶跃响应曲线
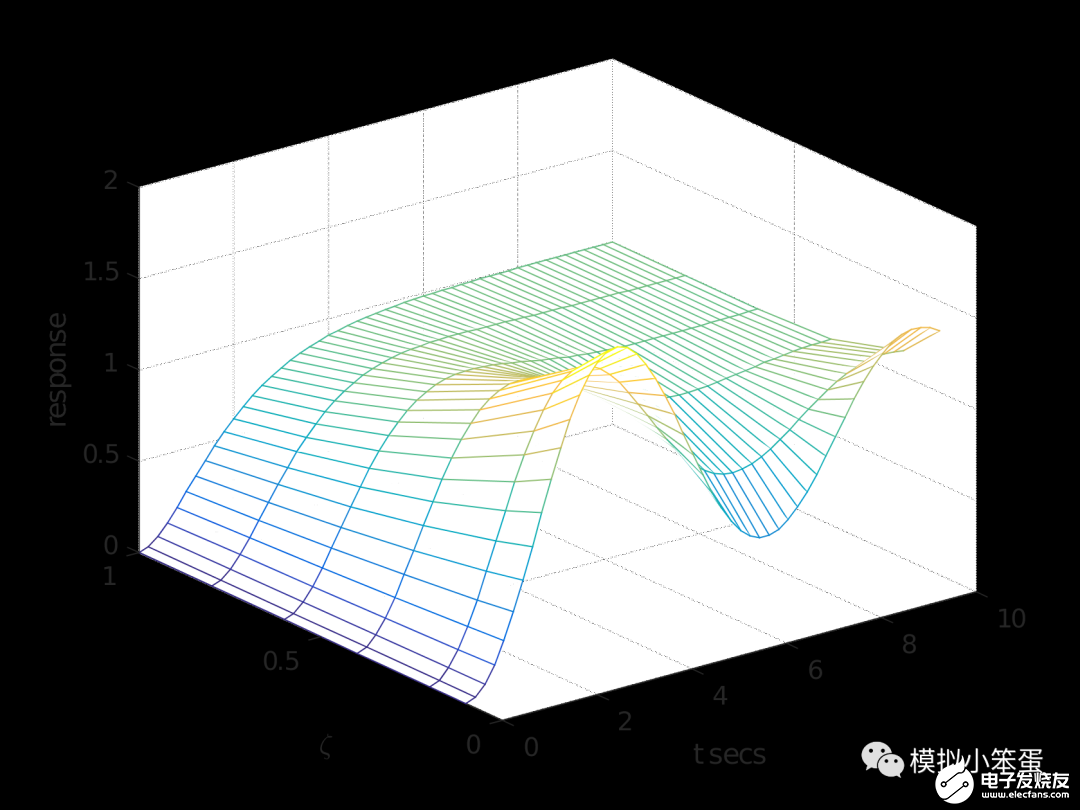
图 2 ζ取不同值时的三维图形
当ζ从0不断增大时,系统将逐渐从欠阻尼状态(0<ζ<1)过渡到临界阻尼状态(ζ=1)再过渡到过阻尼状态(ζ>1)。
观察闭环阶跃响应曲线,当ζ<0.6时,系统表现出很大的减幅振荡;当ζ≥0.6时,系统趋于稳定,可以看到ζ=1.0时已非常稳定。也可以发现,当系统的稳定性有保障之后,响应速度随着ζ越大而越来越慢。在工程控制中,为了平衡系统稳定性和响应速度,ζ一般取0.707。
02 频域
其实也可以在频域上观察系统的稳定性,设计如下的Matlab代码,仿真结果如图3所示。
% G(s)=ωn^2/(s^2+2ζωn s+ωn^2 ).whenωn=1,the plot of bode digram
% with different ζvalues.
%------------------------------------------------------------------------
zt=[0.1 0.2 0.4 0.6 0.8 1];
%zt=[0.1:0.1:1];
for n=1:6;
num=[1];
den=[1 2*zt(n) 1];
G=tf(num,den);
hold on;
bode(G)
end
grid
title(‘plot of bode diagram with omega_n=1 and zeta=0.1,0.2,0.4,0.6.0.8,1.0’)
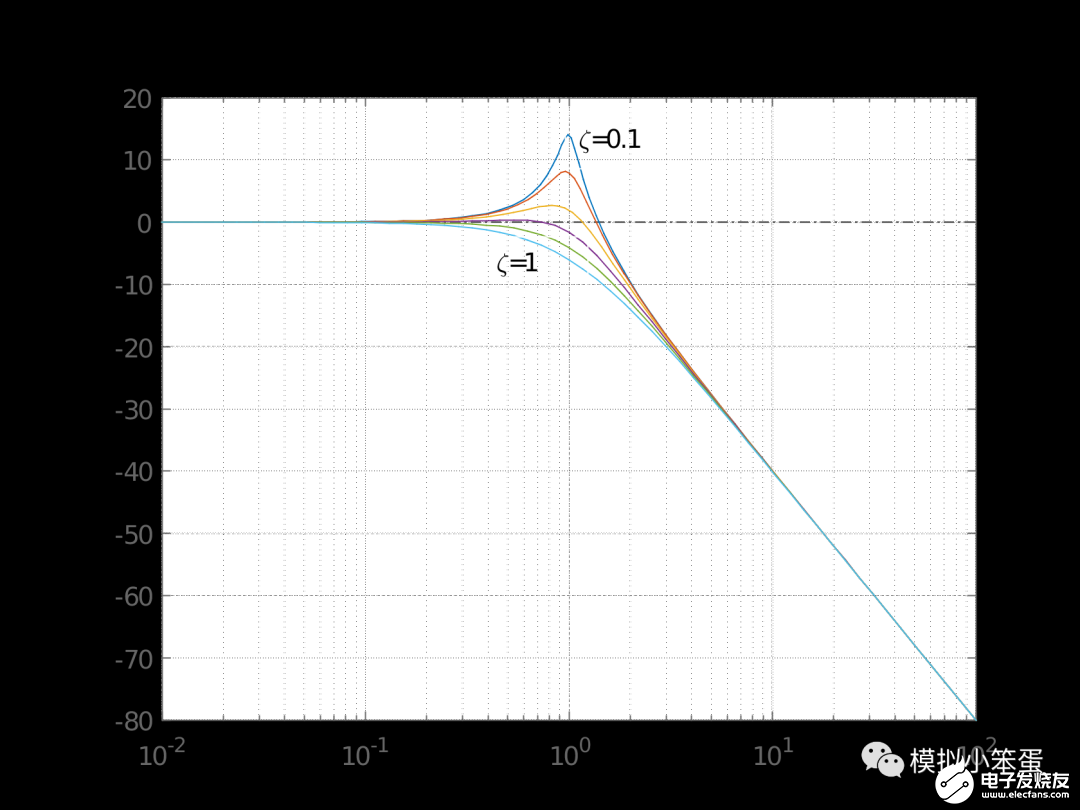
图 3 ζ取不同值时的闭环频率响应曲线
观察闭环频率响应曲线,因为ωn=1,发现1rad/s附近有好几条曲线具有正的增益,这其实是系统不稳定的表现。重点观察ζ=0.1时的曲线,因为ωn=1时,所以曲线在大约1rad/s处出现尖峰(意味着极大增益),实际会表现为振荡。同理,如果ωn=2,ζ=0.1时曲线会在2rad/s附近出现尖峰。(注:如果ζ=0,会发现在ωn处有无穷大增益)。工程控制中一般取ζ=0.707是非常有道理的,此时系统在稳定性和响应速度方面可以说达到了最好平衡。此时,闭环系统的频响平坦区范围基本上是0~ωn。
03 总结
ζ=0.707时,系统的稳定性和响应速度之间达到最好的折衷,此时闭环频率响应的平坦区范围可到ωn;
ζ=0.707不一定是所有二阶系统的最优选择 ,在稳定性得到保障之后,ζ具体取多大还要看实际系统的具体需求;
一个不稳定的二阶系统,很可能会在ωn附近出现振荡行为;
使用Matlab可以对任意已知传递函数的系统进行阶跃响应、脉冲响应、斜坡响应的分析。脉冲响应可直接使用impulse(num,den,t)命令。斜坡响应较为复杂,没有直接的命令可用。这时就需要进行公式转换,斜坡响应的拉普拉斯表示为1/s2,将其乘以G(s)得到G(s)/s2,因此G(s)的斜坡响应可通过G(s)/s的阶跃响应得到。
参考:
[1] 现代控制工程,Katsuhiko Ogata,P123~P149
[2] 控制系统计算机辅助设计,薛定宇,P170~P190
审核编辑:黄飞
-
matlab
+关注
关注
186文章
2983浏览量
231209 -
函数
+关注
关注
3文章
4350浏览量
63051 -
代码
+关注
关注
30文章
4841浏览量
69196 -
时域分析
+关注
关注
0文章
35浏览量
11119 -
闭环系统
+关注
关注
0文章
17浏览量
9453
发布评论请先 登录
相关推荐
基于Matlab/Simulink的二阶控制系统仿真研究
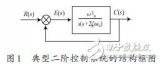
二阶系统动态特性的时频虚拟测试
复杂水电系统二阶振荡模式
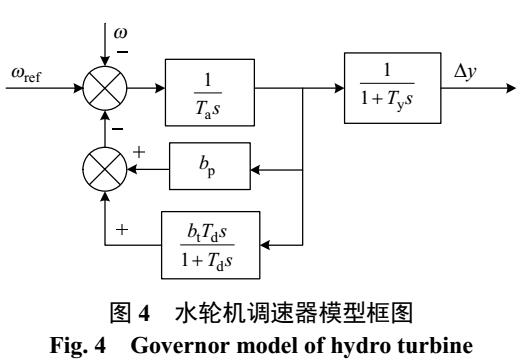
一阶电路和二阶电路的时域分析详细资料概述免费下载
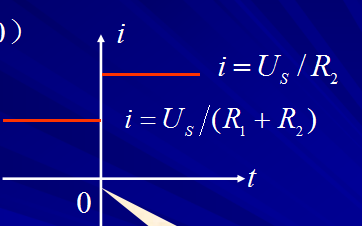
模拟电路设计之二阶系统的瞬态响应分析




 标准二阶系统的Matlab代码示例分析
标准二阶系统的Matlab代码示例分析












评论