上一节讲到了根据PIN1的边界条件求解系数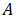 和
和 ,下面根据PIN2的边界条件求解系数
,下面根据PIN2的边界条件求解系数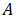 和
和
首先,阳极侧 的边界条件与PIN1相同,即阳极电子电流为0,即
的边界条件与PIN1相同,即阳极电子电流为0,即 ;
;
其次,阴极侧 的边界条件与PIN1不同,阴极侧因PN结反偏,空穴浓度为0,即
的边界条件与PIN1不同,阴极侧因PN结反偏,空穴浓度为0,即 。
。
(这里需要注意的是,载流子电流为零并不意味着载流子浓度为零,反之亦然。对于PIN1结构,因为阳极和阴极的多子浓度远大于少子浓度,所以可以忽略少子电流;对于PIN2结构,因为阴极PN结反偏的缘故,载流子被耗尽,所以浓度为零,但因电场和浓度差的存在,电流却不为零。)
将上述两个边界条件带入 的通解表达式,即可得到系数
的通解表达式,即可得到系数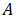 和
和 电流密度
电流密度 之间的关系如下:
之间的关系如下:

将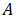 和
和 带入
带入 的通解表达式,整理后便得到PIN2的浓度分布:
的通解表达式,整理后便得到PIN2的浓度分布:

同理,假设载流子寿命为1 ,芯片厚度为100
,芯片厚度为100 ,电流密度为
,电流密度为 时,载流子浓度如图所示。显然,阳极(集电极)区域载流子浓度最高,在N-drift区域逐渐降低,直至到0。
时,载流子浓度如图所示。显然,阳极(集电极)区域载流子浓度最高,在N-drift区域逐渐降低,直至到0。

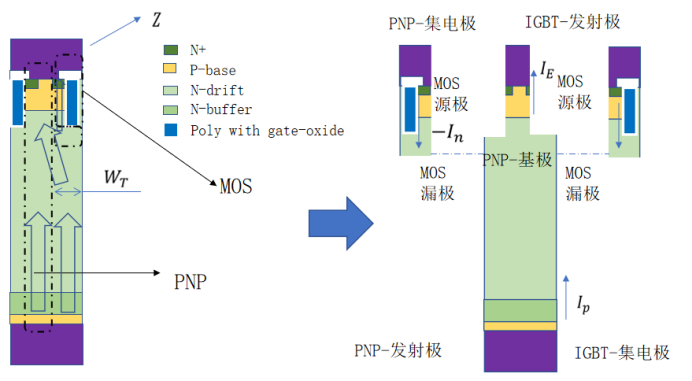
对应IGBT结构(如图虚线区域顺时针旋转90°),阴极区域对应p-base基区,即载流子到达基区底部时,其浓度会降低至0,所以基区底部是没有电导调制效应的。
在实际设计中,设计人员也会通过一些技术手段来增强这个区域载流子的浓度。当然,这也会对其他参数造成影响,如击穿电压等,设计中需要综合考虑。
把PIN1和PIN2的载流子浓度分布绘到一起如图所示,可以清晰地看出IGBT红色阴影部分的载流子浓度是很低的。

同时,从浓度分布曲线上还可以发现其他一些现象:
集电极的载流子浓度并非均匀分布,PIN1区域的浓度要略高于PIN2区域。考虑到实际加工过程中,集电极的浓度是相同的,又因为集电极侧的电子电流为0,这就意味着PIN1区域的空穴注入效率要高于PIN2区域;
因为横向载流子浓度的不同,所以在IGBT内部一定会形成横向的扩散电流,在靠近集电极一侧,横向扩散自PIN1区域向PIN2方向,在靠近p-base基区一侧,横向扩散自PIN2区域向PIN1区域。
-
IGBT
+关注
关注
1267文章
3811浏览量
249423 -
MOS
+关注
关注
32文章
1279浏览量
93981 -
PN结
+关注
关注
8文章
483浏览量
48802 -
击穿电压
+关注
关注
1文章
59浏览量
9033 -
载流子
+关注
关注
0文章
134浏览量
7671
发布评论请先 登录
相关推荐
高压MOSFET与IGBT SPICE模型
无纹波控制系统仿真结构模型
IPTV的系统结构模型





 IGBT的物理结构模型—PIN&MOS模型(3)
IGBT的物理结构模型—PIN&MOS模型(3)

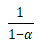
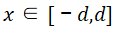











评论