在《IGBT的物理结构模型》中,我们将IGBT内部PIN结切分成了PIN1和PIN2(见上一节插图), 因为PIN1与沟槽所构成的MOS串联,而IGBT关断是通过MOS沟道夹断而关断,而分析PIN1时所采用的边界条件为阴极只有电子电流,空穴电流为0,因此PIN1部分的电流随着MOS关断会迅速降低到0,对后续关断瞬态的分析影响很小。
而PIN2部分的电流则会通过复合缓慢衰减,是后续关断中电流的主要构成部分,因此这里我们只讨论PIN2的稳态和瞬态过程。
在之前的分析中,我们采用了对称的一维坐标体系,即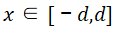 ,对稳态的载流子浓度分布进行推导。考虑到关断瞬态过程中,耗尽区会逐渐扩大,基于该坐标体系的
,对稳态的载流子浓度分布进行推导。考虑到关断瞬态过程中,耗尽区会逐渐扩大,基于该坐标体系的 部分会逐渐减小,即非耗尽区逐渐减小,不再相对中点对称,显然对称坐标体系不便于后续的梳理推导。这里我们先更换坐标体系为
部分会逐渐减小,即非耗尽区逐渐减小,不再相对中点对称,显然对称坐标体系不便于后续的梳理推导。这里我们先更换坐标体系为 ,其中
,其中 为非耗尽区宽度,重新求解扩散方程(6-2),并将结果作为后续关断瞬态的初始条件。
为非耗尽区宽度,重新求解扩散方程(6-2),并将结果作为后续关断瞬态的初始条件。

如图所示,假设IGBT基区宽度为 ,回顾《IGBT中的若干PN结》中关于反偏PN结的耗尽区宽度计算,显然,
,回顾《IGBT中的若干PN结》中关于反偏PN结的耗尽区宽度计算,显然,

其中, 为base区掺杂浓度,
为base区掺杂浓度,  为BJT基极与集电极之间的反偏电压。需要注意的是该等式中忽略了内建电势以及p-base的浓度影响。在导通状况下,
为BJT基极与集电极之间的反偏电压。需要注意的是该等式中忽略了内建电势以及p-base的浓度影响。在导通状况下,  近似认为0,但关断过程中,主要依靠
近似认为0,但关断过程中,主要依靠 所在位置的反偏PN结承受电压,近似认为
所在位置的反偏PN结承受电压,近似认为 等于外界施加电压。
等于外界施加电压。
回顾《IGBT的物理结构模型》的PIN结构模型,取阳极边界条件(IGBT集电极)为电子电流 ,在这里即
,在这里即 ,其中
,其中 表示总电流。为简化运算,直接令
表示总电流。为简化运算,直接令 (稍后我们会给出
(稍后我们会给出 与
与 之间的关系),这样边界条件根据坐标系的变更调整如下:
之间的关系),这样边界条件根据坐标系的变更调整如下:

(6-2)的通解是  ,根据边界条件(6-8),很容易计算出通解的系数
,根据边界条件(6-8),很容易计算出通解的系数 和
和 分别为:
分别为:

将系数 和
和 分别带入
分别带入 的通解表达式,并利用
的通解表达式,并利用 ,可以得出稳态下
,可以得出稳态下 的表达式:
的表达式:

下面我们看看 与电流
与电流 之间的关系。在
之间的关系。在 处,将(6-10)求微分,然后将结果带入边界条件
处,将(6-10)求微分,然后将结果带入边界条件 ,得到:
,得到:

所以,当通过IGBT的总电流 确定后,通过(6-10)和(6-11)即可计算出IGBT内部任意位置的多余载流子分布。
确定后,通过(6-10)和(6-11)即可计算出IGBT内部任意位置的多余载流子分布。
需要注意的是,上述分析均是基于大注入的模型假设,即任意位置 均成立,但是显然在接近BJT集电极的位置,因为PN结反偏,
均成立,但是显然在接近BJT集电极的位置,因为PN结反偏,  ,所以大注入条件在这个位置是不成立的。
,所以大注入条件在这个位置是不成立的。
尽管如此,这个区域占比很小,因此大注入模型依然能够比较准确地分析 和电流分布的影响。
和电流分布的影响。

后面,基于稳态的 分布,我们将逐一构建起电流(包括电子电流和空穴电流)、电压与
分布,我们将逐一构建起电流(包括电子电流和空穴电流)、电压与 之间的关系,再通过
之间的关系,再通过 与
与 或者
或者 之间的关系,并将其作为后续关断瞬态分析的边界条件。
之间的关系,并将其作为后续关断瞬态分析的边界条件。
图中绘出了 随总电流
随总电流 的变化趋势, 横坐标
的变化趋势, 横坐标 处的载流子浓度即为
处的载流子浓度即为 ,显然
,显然 随
随 增大而增大。(6-11)所给出的
增大而增大。(6-11)所给出的 与
与 的关系是基于PIN结构模型
的关系是基于PIN结构模型 。但实际上基于BJT模型,存在基极的电子电流
。但实际上基于BJT模型,存在基极的电子电流 ,这部分电流电流必须要经过BJT发射极(IGBT集电极)流出,所以
,这部分电流电流必须要经过BJT发射极(IGBT集电极)流出,所以 。下面我们会再基于BJT结构模型来进一步修正
。下面我们会再基于BJT结构模型来进一步修正 、
、 与
与 的关系。
的关系。
-
IGBT
+关注
关注
1270文章
3863浏览量
250895 -
MOS
+关注
关注
32文章
1302浏览量
94702 -
PN结
+关注
关注
8文章
486浏览量
49109 -
载流子
+关注
关注
0文章
134浏览量
7725 -
BJT管
+关注
关注
0文章
74浏览量
6451
发布评论请先 登录
相关推荐
IGBT并联技术分析
功率变换器中的功率磁性元件分布参数
离子计数法的直流线路空间电荷密度测量

开关电源变换器稳态原理分析(电感伏秒平衡及电容电荷平衡)





 IGBT稳态分析—电流与电荷分布的初步分析(3)
IGBT稳态分析—电流与电荷分布的初步分析(3)
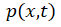
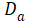
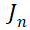
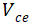
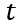











评论