前面我们基本完成了稳态状况下,电流(包含电子电流和空穴电流)与电荷分布之间的关系,下面我们来看看稳态下电压与电荷分布之间的关系。
与之前分析逻辑相似,我们只需建立电压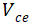 与
与 关系即可。
关系即可。

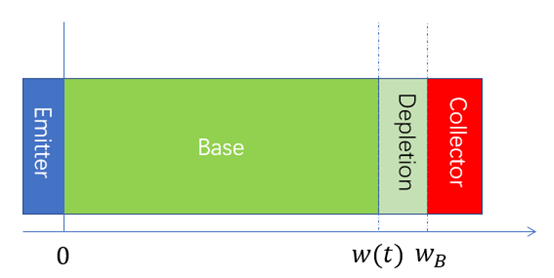
摘录本章第2节截图,显然IGBT导通过程中的电压构成为,

因为导通过程中,耗尽区(Depletion Area)很窄,所以 近似认为0;
近似认为0; 在《IGBT的MOS结构》中已经详细分析,只需将沟道电阻乘以沟道电流即可,而沟道电流即为
在《IGBT的MOS结构》中已经详细分析,只需将沟道电阻乘以沟道电流即可,而沟道电流即为 ,即
,即

其中,A为芯片面积,  为导通情况下,MOS的沟道电阻,表达式如下,
为导通情况下,MOS的沟道电阻,表达式如下,

因此,欲建立稳态下,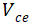 与
与 的关系,只需建立稳态下
的关系,只需建立稳态下 与
与 的关系。下面重点对
的关系。下面重点对 进行分析。
进行分析。
显然, 由两个部分构成,即BJT发射极的PN结结电压以及电流流经Base区域的欧姆电压,定义这两个电压为
由两个部分构成,即BJT发射极的PN结结电压以及电流流经Base区域的欧姆电压,定义这两个电压为 和
和 。在《IGBT中的若干PN结》中,我们对结电压做过推演(也可参考本章(6-14)式),这里直接采用结论如下,
。在《IGBT中的若干PN结》中,我们对结电压做过推演(也可参考本章(6-14)式),这里直接采用结论如下,

上式采用了大注入近似条件(  ),(6-25)准确地建立了
),(6-25)准确地建立了 与
与 之间的关系,接下来就只剩下建立
之间的关系,接下来就只剩下建立 与
与 之间的关系。在推演它们之间的数理关系之前,有必要先澄清一个概念,即欧姆电压的来源。
之间的关系。在推演它们之间的数理关系之前,有必要先澄清一个概念,即欧姆电压的来源。
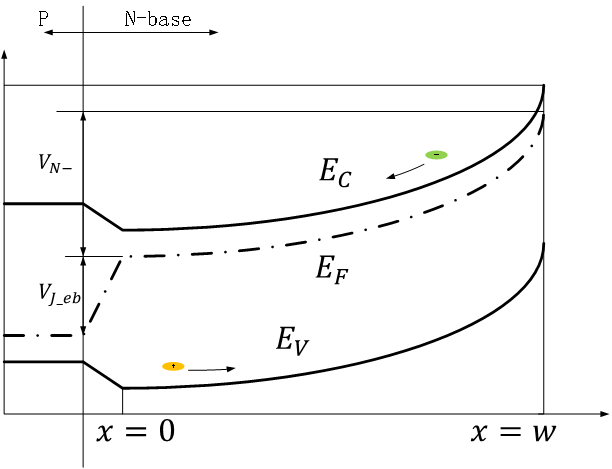
根据泊松方程,电压是电场的积分,电场是电荷的积分,那么N-base区域为电中性区域,那么该区域中不存在净电荷,那么就不应该存在电场,也就不应该有电势差(电压)那么为什么会有欧姆电压呢?而且,在扩散方程的建立中,也采用了电中性原则,只计入了扩散电流,未计入电场相关的漂移电流。
事实上,上述物理描述只对电荷引起的电场和电势差进行了描述,但还缺少对电荷周期排布所引入的能级电势差。回顾《电荷变化》一章,我们分析了半导体中还有因电荷周期排布而存在的能级关系,以费米能级为特征能级,不同能级相对费米能级的距离(能量差),决定了被电荷占有的概率。
无论是扩散电流还是漂移电流,追溯到本质,都可以理解为因费米能级的变化而导致导带和价带被电子/空穴占有概率的变化,从而表现出电荷流动的现象。因此,欧姆电压可理解为N-base区域的费米能级变化所引入的电势差。
-
IGBT
+关注
关注
1267文章
3793浏览量
249007 -
PN结
+关注
关注
8文章
481浏览量
48728 -
BJT
+关注
关注
0文章
222浏览量
18163
发布评论请先 登录
相关推荐




 IGBT电压与电荷分布之间的关系(1)
IGBT电压与电荷分布之间的关系(1)
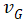
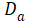
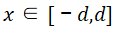
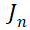











评论