因为电子从费米能级高位向低位流动,因此根据电子电流的流向很容易绘出费米能级的弯曲方向,这里将BJT发射极到集电极的导带及价带能带示意图绘制如图所示。
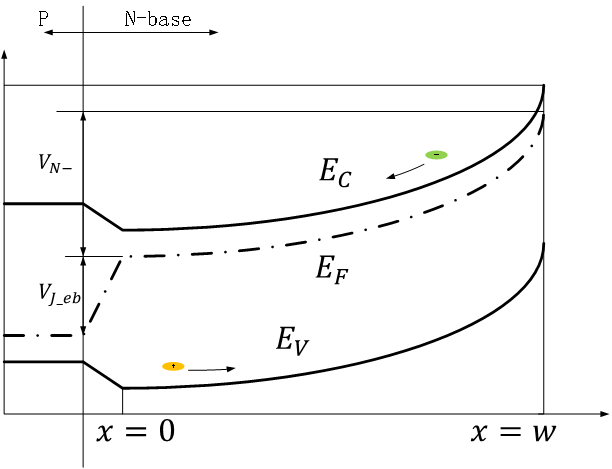
费米能级弯曲的变化率(费米电势梯度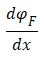 )所引起的电子电流为,
)所引起的电子电流为,
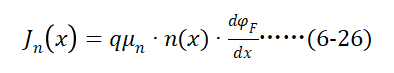
其中, 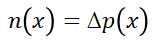 ,因此欧姆电压
,因此欧姆电压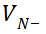 就是费米电势从
就是费米电势从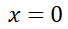 到
到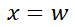 的积分。
的积分。
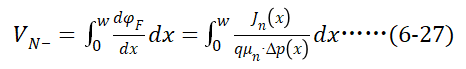
下面,我们通过电子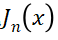 总电流
总电流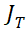 关系、多余空穴浓度分布
关系、多余空穴浓度分布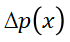 与边界处空穴浓度
与边界处空穴浓度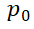 之间的关系,以及
之间的关系,以及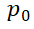 与总电流
与总电流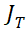 关系关系,即可准确地推演出
关系关系,即可准确地推演出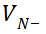 与总电流
与总电流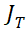 的关系。
的关系。
上述过程可以通过将(6-6)以及(6-10)带入(6-27),并稍作整理得到如下表达式,
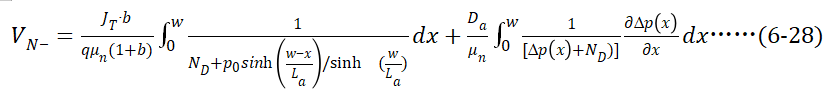
需要注意的是,(6-28)中右边积分项分布中没有因为大注入假设而省去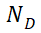 ,否则当
,否则当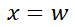 时会出现分母为0的情况。下面分别对(6-28)右边两项积分,分别将右边第一项和第二项定义为
时会出现分母为0的情况。下面分别对(6-28)右边两项积分,分别将右边第一项和第二项定义为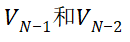 。
。
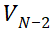 很容求积分,如下,
很容求积分,如下,
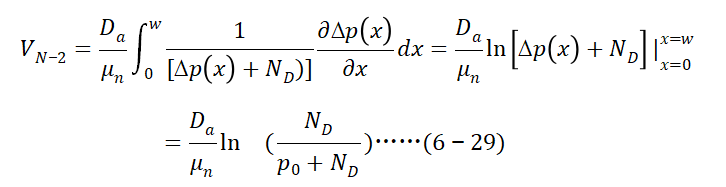
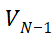 积分过程相对繁琐,这里就不逐步进行推演了,感兴趣的读者可以尝试推导。
积分过程相对繁琐,这里就不逐步进行推演了,感兴趣的读者可以尝试推导。
新定义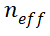 为有效电子浓度,其表达式如下,
为有效电子浓度,其表达式如下,
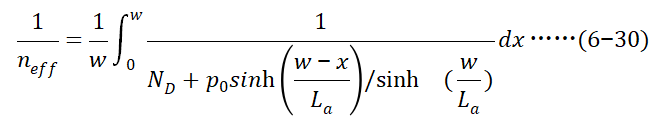 从而
从而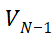 可表达为,
可表达为,
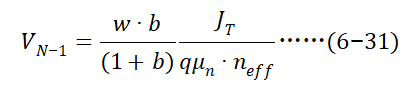
从(6-31)可以看出 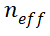 的物理意义,
的物理意义, 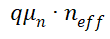 表征了电导率,所以
表征了电导率,所以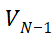 可以理解为对电导率的修正,即电导调制效应。
可以理解为对电导率的修正,即电导调制效应。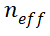 的积分结果为(过程省略),
的积分结果为(过程省略),
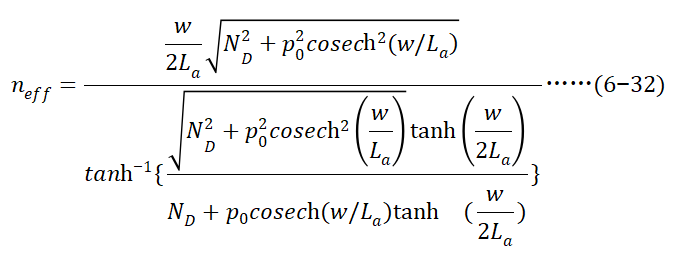 经过前面的推导,可以准确地将
经过前面的推导,可以准确地将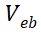 表达如下:
表达如下:
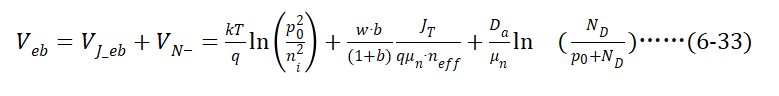
因此,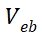 由三个部分构成,(6-33)右边第一项为结电压,第二项为经电导调制效应的欧姆电压 ,第三项为大注入下因电荷浓度分布而产生的扩散电压。
由三个部分构成,(6-33)右边第一项为结电压,第二项为经电导调制效应的欧姆电压 ,第三项为大注入下因电荷浓度分布而产生的扩散电压。
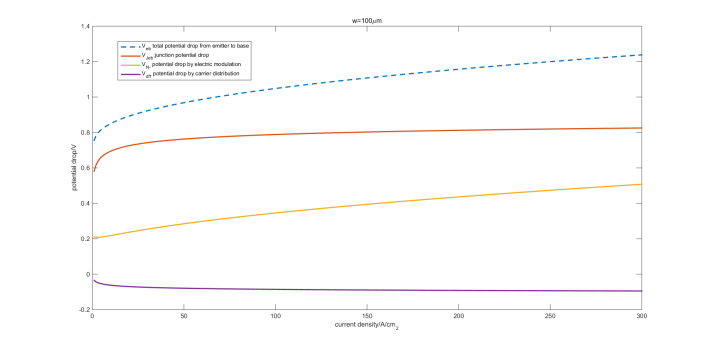
举例,还是采用前面相同的物理结构参数,调整总电流浓度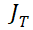 从
从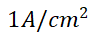 到
到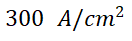 ,观察上述三个电压构成随电流密度的变化趋势,如图所示。
,观察上述三个电压构成随电流密度的变化趋势,如图所示。
可以看出,随着电流密度的增加,结电压变化幅度很小,电压增长主要来自于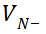 部分。
部分。
结电压和扩散电压存在明显的饱和趋势,而欧姆电压则几乎呈线性增长趋势。读者如果感兴趣,可以尝试改变迁移率等其他变量,观察不同电压构成随电流密度的变化趋势。
至此,我们完整地建立了稳态下电压、电流与电荷浓度分布之间的关系,它们将作为下面瞬态分析的初始条件。
-
IGBT
+关注
关注
1266文章
3788浏览量
248839 -
BJT
+关注
关注
0文章
222浏览量
18153 -
电压电流
+关注
关注
1文章
167浏览量
12434
发布评论请先 登录
相关推荐




 IGBT电压与电荷分布之间的关系(2)
IGBT电压与电荷分布之间的关系(2)
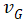
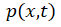
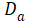
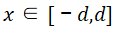
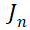
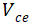

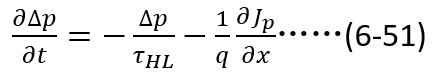










评论