在稳态部分的分析中,我们详细地推演了电子电流、空穴电流、总电流以及各电压构成部分与多余载流子浓度分布之间的关系,即一维空间的物理关系。
接下来,我们引入时间变量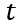 ,进入瞬态部分的分析。
,进入瞬态部分的分析。
当外部栅极控制电压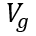 降低到阈值电压
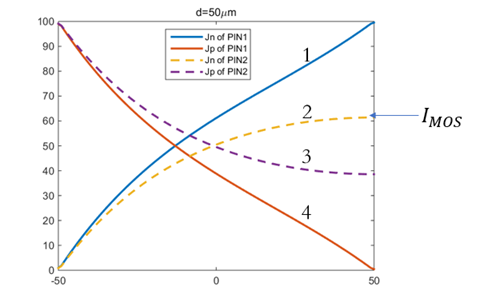
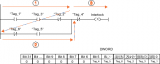
降低到阈值电压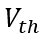 以下时,MOS部分的沟道立即闸断,相应的电子电流变为0,借鉴《电流与电荷分布的初步分析1》中的插图,即图中
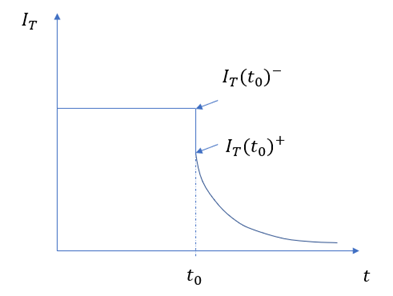
以下时,MOS部分的沟道立即闸断,相应的电子电流变为0,借鉴《电流与电荷分布的初步分析1》中的插图,即图中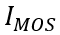 瞬间衰减为0,那么总电流就只剩下如图2、3、4三个部分。
瞬间衰减为0,那么总电流就只剩下如图2、3、4三个部分。
假设这个变化的时间为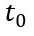 ,变化前后的总电流记为
,变化前后的总电流记为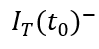 和
和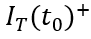 ,描绘总电流在
,描绘总电流在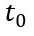 时刻发生突变。
时刻发生突变。
显然, 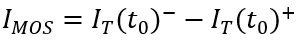 ,下一节我们会具体地讨论
,下一节我们会具体地讨论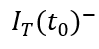 和
和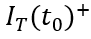 的关系。
的关系。
推演电流和电压随时间的变化关系的大致逻辑是:电流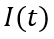 是器件内部电荷总量
是器件内部电荷总量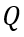 在时间维度为微分
在时间维度为微分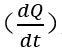 ,电荷总量
,电荷总量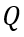 是载流子
是载流子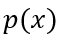 的积分,
的积分,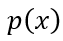 可以通过连续方程求解得出,其边界条件为非耗尽区两端的电荷浓度,即
可以通过连续方程求解得出,其边界条件为非耗尽区两端的电荷浓度,即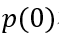 和
和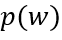 ,求解方法参考前面稳态部分。
,求解方法参考前面稳态部分。
与稳态部分不同的是,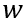 随时间变化,记为
随时间变化,记为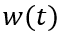
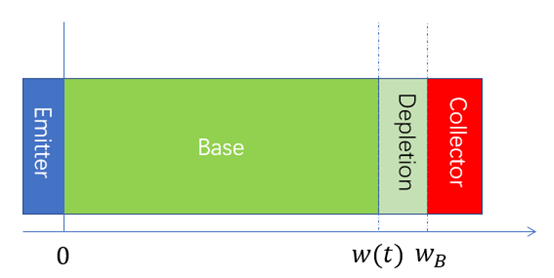
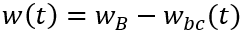 ,其中
,其中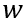 是base区宽度,
是base区宽度, 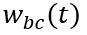 是耗尽区宽度;
是耗尽区宽度;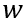 是固定值,
是固定值,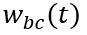 随外加电压
随外加电压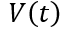 变化,根据泊松方程,
变化,根据泊松方程,
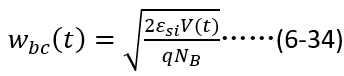
由此,根据稳态部分的边界条件,我们就可以准确地推演出关断瞬态过程中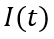 和
和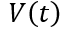 的关系。下面,我们根据上述逻辑,逐步展开分析,首先看电荷总量
的关系。下面,我们根据上述逻辑,逐步展开分析,首先看电荷总量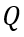 随时间的变化。
随时间的变化。
假设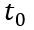 时刻为0时刻,先求解
时刻为0时刻,先求解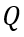 的初始值
的初始值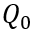 ,这可以通过对稳态下
,这可以通过对稳态下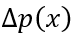 的积分得到,即对(6-10)进行积分,
的积分得到,即对(6-10)进行积分,
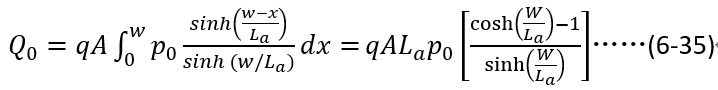
其中,A为芯片面积。分子利用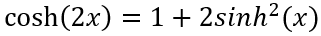 ,分母利用关系
,分母利用关系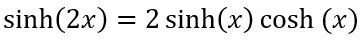 ,(6-35)可以进一步简化为,
,(6-35)可以进一步简化为,
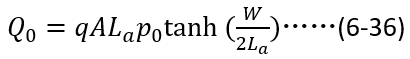
接下来,我们建立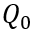 与电流初始条件
与电流初始条件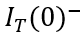 之间的关系,根据(6-36),即要建立
之间的关系,根据(6-36),即要建立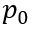 与
与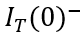 之间关系。
之间关系。
在稳态分析中,我们分别基于PIN模型和BJT模型建立了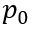 和电流密度
和电流密度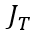 之间的关系(
之间的关系( 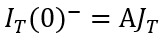 ),这里应该使用哪一个模型的结论呢?如稳态部分所分析,这取决于
),这里应该使用哪一个模型的结论呢?如稳态部分所分析,这取决于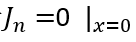 还是
还是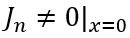 ,而这又取决于电子的载流子寿命,及其对应的扩散长度。
,而这又取决于电子的载流子寿命,及其对应的扩散长度。
当扩散长度大于BJT的基区宽度时,那么电子可以扩散到BJT的发射极,那么显然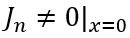 ,应采用BJT模型的结论;反之,电子无法扩散到BJT的发射极,那么
,应采用BJT模型的结论;反之,电子无法扩散到BJT的发射极,那么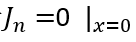 ,应采用PIN模型的结论。
,应采用PIN模型的结论。
为简化后面的运算,这里我们采用基于PIN模型的结论(采用BJT模型也可以,但是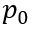 和电流密度
和电流密度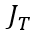 之间的关系就需要通过求解(6-21)来得到,相对复杂,但逻辑相同),即(6-11)所描述的
之间的关系就需要通过求解(6-21)来得到,相对复杂,但逻辑相同),即(6-11)所描述的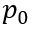 和电流密度
和电流密度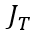 之间的关系,再乘以芯片面积:
之间的关系,再乘以芯片面积:
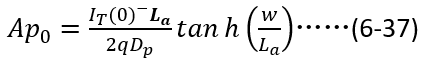
将(6-37)带入(6-36),即可得到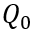 与电流初始条件
与电流初始条件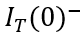 之间的关系,并化简,
之间的关系,并化简,
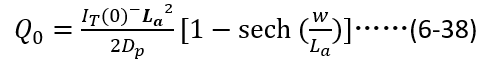
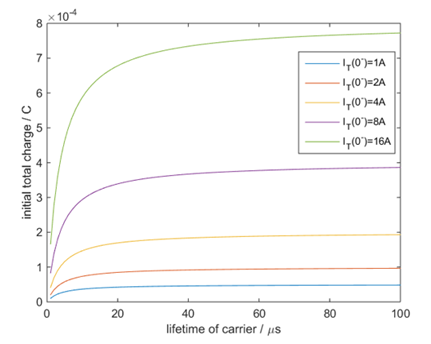
根据(6-38),我们看看初始电荷总量随稳态电流以及载流子寿命之间的变化关系。显然,在稳态电流值确定的情况下,初始电荷总量随载流子寿命增加而趋向饱和。
-
IGBT
+关注
关注
1267文章
3809浏览量
249362 -
MOS
+关注
关注
32文章
1278浏览量
93937 -
BJT
+关注
关注
0文章
237浏览量
18208 -
载流子
+关注
关注
0文章
134浏览量
7669 -
阈值电压
+关注
关注
0文章
73浏览量
51457
发布评论请先 登录
相关推荐
抑制初始值的警告
换路定律及初始值的确定
浅析MCU内部的RAM上电之后的初始值相关问题
教你们怎么去设定寄存器的初始值

如何保证MCU上电后RAM的初始值唯一

如何保证MCU上电后RAM的初始值唯一

关于对IGBT关断过程的分析





 IGBT的关断瞬态分析—电荷存储初始值
IGBT的关断瞬态分析—电荷存储初始值

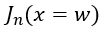











评论