设计单向射频放大器时增益分析的重要性

关键要点

RF放大器设计需要考虑增益分析，通过计算输入和输出反射系数可以确定电路的增益。

放大器的增益可以使用传感器功率增益来衡量，它是基于电路输入和输出功率的比值。

在设计过程中，可以使用常量增益圆来确定输入和输出反射系数的合适值以实现所需的增益。

概要

本文介绍了在设计单向射频放大器时增益分析的重要性。首先，在低频放大器的分析相对简单，因为不需要考虑信号反射。然后，介绍了传感器功率增益的概念和计算方法。文章还详细讨论了单向传感器功率增益的计算和设计过程，并解释了常量增益圆的使用方法。最后，提供了两个示例，演示了如何根据给定的增益设计放大器并通过模拟进行验证。

首先回顾基本概念，然后通过一对设计示例来了解增益分析在单边射频放大器设计中的作用。

与许多其他射频设计主题一样，射频放大器设计的数学密集程度可能令人望而生畏。不过，借助当今的射频设计软件工具，我们不需要花费所有时间将数字代入方程式。相反，我们需要了解这些方程背后的设计原理，以便我们可以自信地使用我们的软件工具。为此，本系列的上一篇文章讨论了射频放大器稳定性分析的基础知识。现在是时候介绍设计过程的另一个重要部分：评估放大器的增益。

分析低频放大器的增益相对简单，因为我们不需要担心低频信号反射。在非常低的频率下，我们可以通过假设晶体管是单边的来进一步简化我们的分析，这意味着从其输出到输入没有内部反馈。

换能器功率增益

在设计放大器时，我们将传感器功率增益用于射频二端口网络。要了解传感器功率增益，请考虑图 1 中的射频放大器原理图。

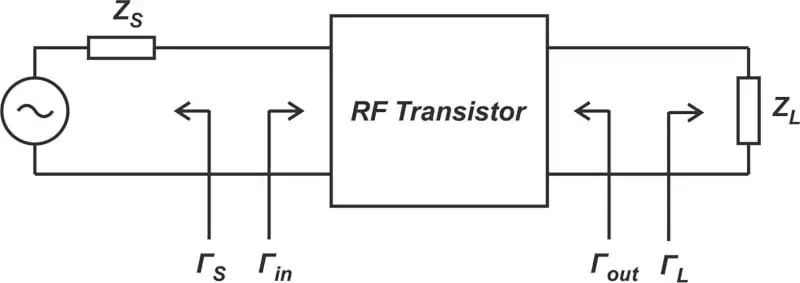
图 1.具有任意源阻抗和负载阻抗的 RF 单级放大器。

换能器功率增益 (GT)定义为：

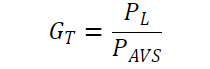
等式 1。

在哪里：

PL是输送到负载的功率

PAVS是来自电源的可用功率。

PL很容易理解——它只是当晶体管由阻抗为ZS的源极驱动时电路向负载提供的功率。PAVS的构成可能有点令人困惑。PAVS是电源传送至阻抗为 Z s*的共轭匹配负载的功率。下图显示了我们如何确定PAVS。

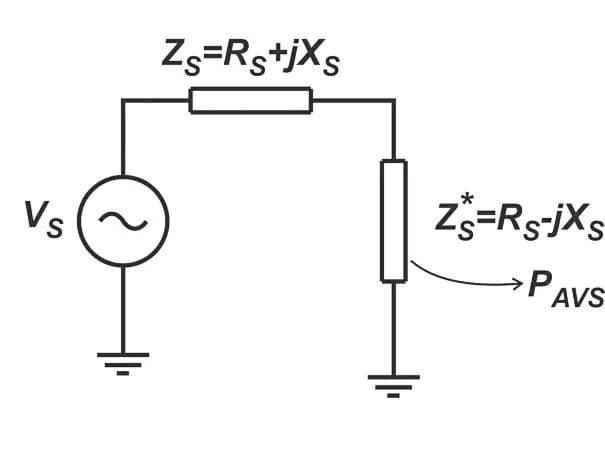
图 2.具有共轭匹配负载的简单射频电源电路。

我们可以使用以下有点令人生畏的方程来用晶体管的 S 参数来表达GT ：

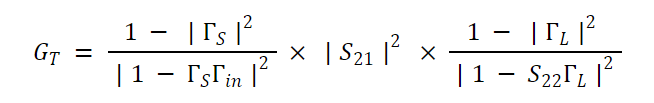
等式2。

其中 ΓIN是晶体管输入端的反射系数，由下式给出：

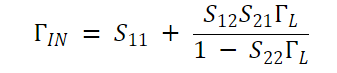
等式 3。

当输入和输出终端均为无反射时，会出现等式 2 的一种特殊情况，这意味着它们匹配零反射 (ГS= ГL= 0)。在这种情况下，换能器功率增益等于 |S21|2.这有时被称为晶体管的“基于Z0的基本换能器功率增益”。

单边换能器功率增益

我们可以看到GT取决于源 (ГS) 和负载 (ГL) 的不匹配。如果我们知道 ГS和 ГL，我们可以使用方程 2 和 3 来计算电路的增益。然而，大多数设计问题要求我们确定给定增益 (GT ) 的 ΓS和 ΓL的值。在这种情况下，直接使用公式 2 可能会有点棘手，因为正如我们在公式 3 中看到的那样，输入和输出反射系数值之间存在相互作用。

在一些实际的放大器电路中，我们可以忽略晶体管内部反馈的影响，并假设S12= 0。在这种情况下，该器件被称为单向器件，并且ΓIN简单地等于S11（见公式3）。这将GT简化为：

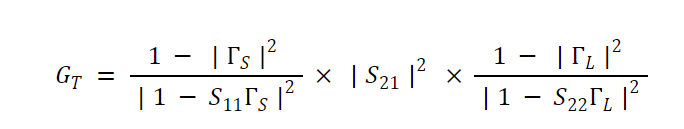
等式 4。

请注意，单边换能器功率增益由三个不同的、独立的增益项组成。

公式 4 如何简化设计过程？假设我们要使用单边器件设计一个 18 dB 单级放大器 |S21|= 6.5。对于此示例，|S21|2= 16.26 分贝。因此，上式中的小数项应提供 1.74 dB 的增益。

由于这两个小数项彼此独立，因此我们可以轻松地将剩余增益分开，并找到合适的 ΓS和 ΓL值。请注意，这两个小数项具有相同的形式，这意味着我们可以开发一个过程来查找 ΓS和 ΓL。

增益项的物理解释

我们可以将等式 4 中的单边增益写为下面定义的三个增益项的乘积：

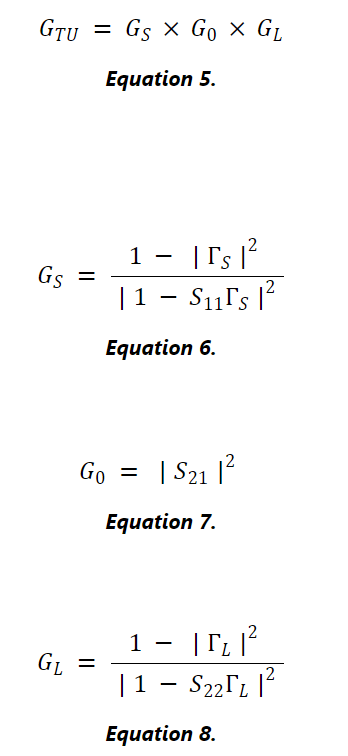
如您所见，GS仅与输入参数（ΓS和S11）相关，而GL仅与输出参数（ΓL和S22）相关。

我们可以将GS和GL解释为输入或输出匹配网络产生的增益或损失。基于此，我们可以将单级放大器建模为具有增益GS、G0和GL的三个模块的级联（图 3）。

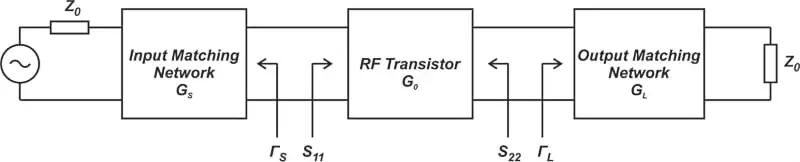
图 3.使用输入和输出匹配网络的单级放大器模型。

但由无源元件组成的匹配网络如何产生增益呢？要理解这种看似矛盾的行为，请注意，当 ГS和S11（在输入处）或 ГL和S22（在输出处）不匹配时，我们可能会出现显着的失配损失。匹配网络提供的更好的阻抗匹配可以减少失配损耗，有效提高增益。

增益项的最小值和最大值

在设计放大器时，重要的是要知道GS和GL各自可以提供多少增益，以便我们可以适当地分配两项之间的总增益。假设|S11|< 1， G S的最大值为：

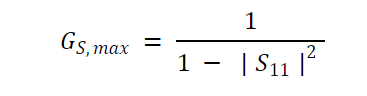
方程 9.

我们一直在研究GS项的范围，但类似的讨论也适用于GL项- 两个增益方程都采用相同的形式。

在本文中，我们假设 |S11|< 1 和 | S 22 | < 1. 这是常见的情况，但并非总是如此——对于潜在不稳定的情况，其中 | S 11 | > 1 和 |S22|> 1、请参阅G. Gonzalez 的《微波晶体管放大器：分析与设计》。

确定适当的端接：恒定增益圆

此时，另一个问题出现了：对于给定的增益（ GS或 GL），我们如何确定合适的反射系数（ ΓS或ΓL）？为了简洁起见，我们将跳过推导细节，直接讨论该问题的最终方程。

让我们考虑一下GS项。我们想要找到合适的 ΓS来产生GS=G。有趣的是，有无数个 ΓS值可以产生某个 GS。所有这些 ΓS值都位于称为常数GS圆的圆上。GS=G圆的中心位置为：

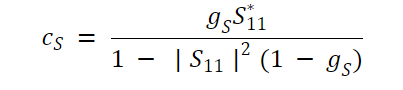
方程 10。

和半径：

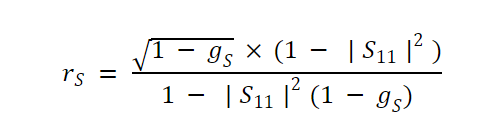
公式 11。

其中gS=G/Gs,max是归一化增益。类似地， GL=G圆的中心由下式给出：

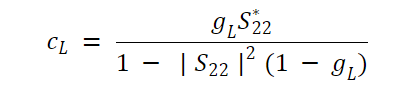
公式 12。

及其半径：

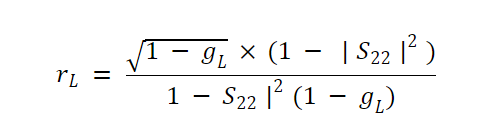
公式 13。

其中gL=G/GL,max是归一化增益。

为了了解这些恒定增益圈的重要特征，让我们通过一些示例计算来进行计算。

示例 1：计算给定频率的增益

假设晶体管的Z0= 50 Ω，其 S 参数如表 1 所示。

表 1.示例晶体管的 S 参数。

f(GHz)	小号11	S21	S12	S22
0.8	0.44∠–157.6	4.725∠84.3	0	0.339∠–51.8
1.4	0.533∠176.6	2.800∠64.5	0	0.604∠–58.3
2.0	0.439∠159.6	2.057∠49.2	0	0.294∠–68.1

首先，我们将找到f= 1.4 GHz时的最大输入和输出匹配部分增益以及最大单边换能器功率增益。之后，我们将绘制该频率下不同GS和GL值的恒定增益圆。

晶体管的基于Z0的基本换能器功率增益为：

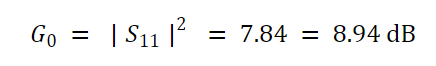
公式 14。

最大匹配部分增益为：

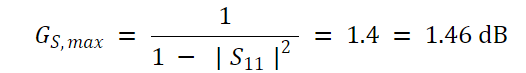
公式 15。

和

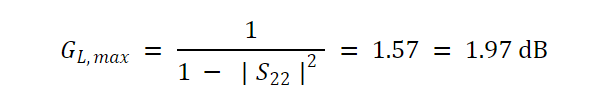
公式 16。

最大传感器增益计算为：

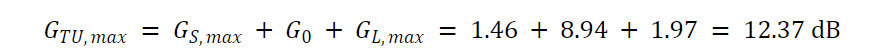
公式 17。

一些恒定GS圆的中心和半径如下表所示。

表 2.恒定GS圆的中心和半径。

获得	归一化增益	中心	半径
GS =0.0分贝	克S=0.71	cS1= 0.41 ∠ –176.6	rS1= 0.41
GS =0.5分贝	克S=0.80	cS1= 0.45 ∠ –176.6	rS1= 0.34
GS=1.0 分贝	克S=0.90	cS2= 0.49 ∠ –176.6	rS2= 0.23
GS =1.4分贝	克S=0.99	cS2= 0.53 ∠ –176.6	rS2= 0.07

图 4 在 ΓS平面上绘制了这些圆。蓝点表示 Γ S=S11*的位置。

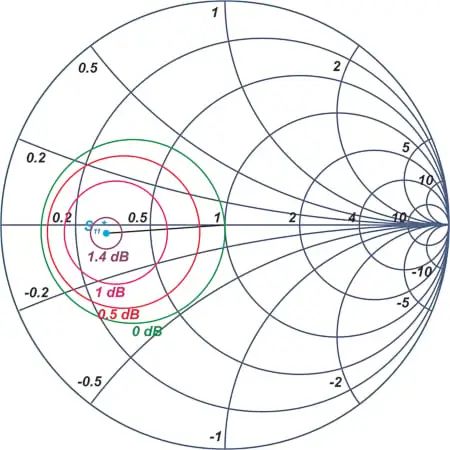
图 4.恒定GS圆。

现在我们已经得到了GS的最大值。观察到常数GS圆的中心都位于连接原点到S11* 的线上。随着增益的增加，增益圆变得更小，并且圆的中心变得更接近S11*。最后，对于增益的最大值，增益圆减小到S11* 处的单个点。

请注意，GS= 1 (0 dB) 圆穿过原点。这并非巧合——对于恒定GS和恒定GL圆来说，这种情况总是会发生。还值得一提的是，我们可以选择 ΓS来产生小于 1 的GS，例如GS= –1 dB。

类似地我们可以求出常数GL圆。表 3 列出了一些示例常数GL圆的中心和半径。

表 3.恒定GL圆的中心和半径。

获得	归一化增益	中心	半径
GL =0.00分贝	克L=0.64	cL1= 0.44 ∠ 58.3	rL1= 0.44
GL=0.66 分贝	克L= 0.74	cL1= 0.49 ∠ 58.3	rL1= 0.36
GL =1.00分贝	克L=0.80	cL2= 0.52 ∠ 58.3	rL2= 0.31
GL=1.56 分贝	克L= 0.91	cL1= 0.57 ∠ 58.3	rL1= 0.20

图 5 在 ΓL平面上绘制了这些圆。

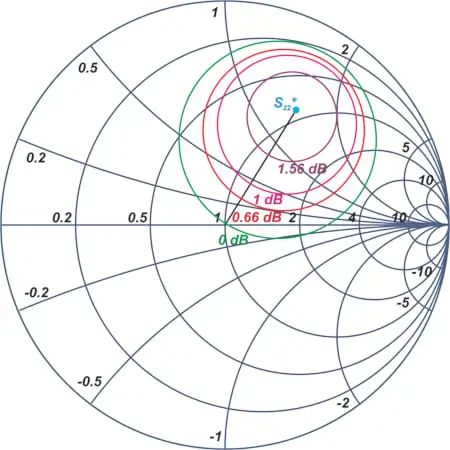
图 5.恒定GL圆。

在恒定GL圆中也可以观察到与针对恒定 G S 圆提到的特征类似的特征。

示例2：根据总增益进行设计

使用前面示例的结果，我们设计一个在 1.4 GHz 时增益为 11 dB 的放大器。

晶体管的基本基于Z0的换能器功率增益是G0= 8.94 dB。因此，要拥有 11 dB 放大器，输入和输出匹配部分应提供 2.06 dB 的总增益。一种可能的解决方案是选择GS= 1 dB 和GL= 1 dB。该设计的增益圆如图 6 所示。

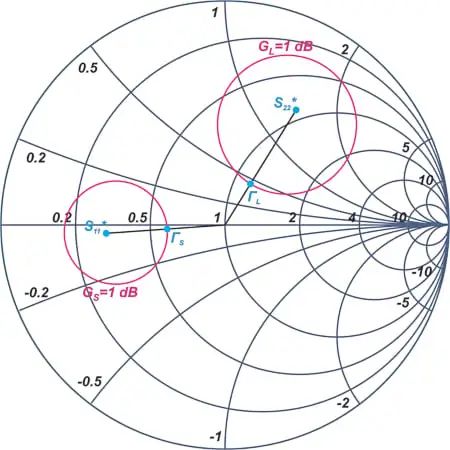
图 6.示例放大器的恒定增益圆。GS和GL均等于1 dB。

这些恒定增益圆上的任何点都可以用来实现所需的总增益。我们将使用上图中所示的反射系数值（ГS和 ГL ）。使用史密斯圆图，我们得到：

伽马S= 0.26 ∠ –176.6

伽马L=0.22∠58.3

图 7 显示了添加了输入和输出匹配部分的最终设计。

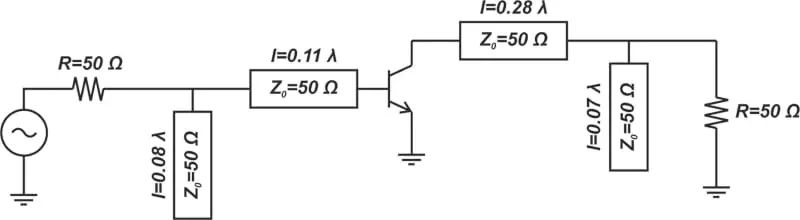
图 7.添加了输入和输出匹配部分的射频放大器。

虽然上图仅显示了交流放大器原理图，但放大器还需要一些偏置电路。此外，我假设有源器件是双极晶体管。

需要温习阻抗匹配技术吗？这篇关于单短截线阻抗匹配的文章可以提供帮助。

图 8 绘制了放大器的模拟增益。

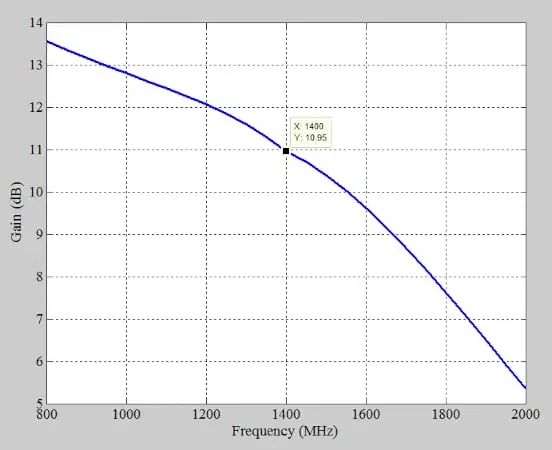
图 8.示例 RF 放大器的增益（y 轴）与频率（x 轴）。

1.4 GHz 时的增益为 10.95 dB，几乎等于所需值。在上述仿真中，软件提供了 0.8、1.4 和 2 GHz 的 S 参数。任何其他所需频率点的 S 参数都是通过插值获得的。放大器的输入反射系数也如下图 9 所示。

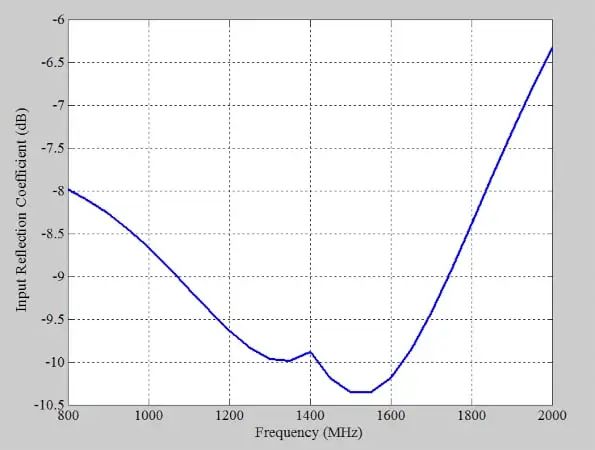
图 9.模拟放大器的输入反射系数（y 轴）与频率（x 轴）的关系。

我们可以看到输入与 50 Ω 源阻抗的匹配不是很好。在此示例中，我们实际上故意降低输入和输出处的阻抗匹配，以将增益降低到所需值。

审核编辑：汤梓红