一文浅述电路系统中的谐振（上）-电子发烧友网

一.起手式

--物理学中的振动概念

第一部分：简谐振动

在物理学中，有一套专门的理论和方法用于振动系统的研究。其中，最基本的振动模型是简谐振动。顾名思义，“简”即“简单，基本”，在这里，我们考虑带弹簧的一维机械系统，“谐振”即“共振”，不同的领域有不同的叫法，“动”表示运动状态。

简谐振动的充分必要条件：物体受到的回复力大小与物体的位移大小成正比，回复力方向与位移方向相反。

翻译成大白话就是，你在向前冲，我把你向后拉，你向前冲的越多，我拉你的劲越大。（这样才能挽留你啊）

简谐振动的动力学描述：

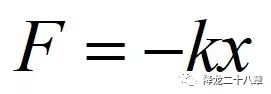
其中，F表示回复力，k为弹性系数，x为物体的位移。

由牛顿第二定律可以知道，此时的回复力可以表示为位移的 二阶导数 ，即：

或者写成：

简谐振动系统是一个二阶系统，其动力学描述是一个 二阶常系数微分方程 。事实上，通过求解二阶常系数微分方程及可以得到其通解。再带入系统的初始条件（初始位移x(0)和初始速度v(0))，即可得到方程的特解。

为了更直观地理解简谐振动，根据微分方程的特解，简谐振动有三种表示方法：解析表示，波形表示和旋转矢量表示。

1.解析表示

直接用微分方程的特解表示：

其中，A为物体做简谐振动的振幅，ω为振动的圆频率（或称角频率），Φ0为初始相位角。

1）物体振动的角频率，仅由系统的本身的的性质决定，在这个场合，由弹性系数k和物体质量m共同决定。

2）至于振幅和初始相位角，则由系统的初始条件（初始位移和初始速度）决定。

3）简谐振动的周期和频率，同样由系统自身的性质决定。相比于角频率，周期和频率更有意义。他们对应了实际物理世界的时间和次数。

2.波形表示

如下图，横轴表示时间，纵轴表示物体的位移，正弦波的周期及为谐振的周期，波形与纵轴的交点即表示初始时刻物体的位置（初始位移），波形上每一点的斜率即为物体的速度。

3.旋转矢量表示

旋转矢量表示法，其原理是匀速圆周运动投影到x轴上正好是余弦函数。之所以要表示成旋转矢量，是为了更方便直观的表示两个状态之间的相位差。该方法常用在同频率的简谐振动的叠加。

以上，我们解释并量化了最基本的一维简谐振动，三种表示方法殊途同归，可视具体场合选用哪种表达。

第二部分：阻尼振动

在实际的物理系统中，简谐振动的情况无法存在，因为系统的能量总是有损耗的，那么对于能量或振动幅度随时间减小的振动，我们称之为阻尼振动。与简谐振动不同，阻尼振动的能量是实时被消耗的。

（注意，这部分需要有高等数学和微分方程的基础，觉得复杂的读者可以忽略下面这些公式的推导，有兴趣的读者可以参考常微分方程的相关知识）

考虑与物体运动速度成正比，方向相反的粘滞阻力（事实上，阻力不一定与速度成严格的正比关系，这里我们简化模型只考虑正比的情况）

此时物体在回复力与阻力一起作用下的运动方程为：

可以看到，物体的运动方程仍然是一个二阶常系数微分方程，如果初始条件确定，该方程在数学上是有严格的解析解的。不过这里我们更关心方程的解的物理意义。下面分为三种情况讨论阻尼振动的形式：弱阻尼（或称欠阻尼）、过阻尼、临界阻尼。由以下五张图片介绍。

实际上，这样的阻尼振动形式不仅存在于机械系统中，在控制理论，电子电路等各个领域中也是常见。本文的主体部分即是将各种谐振形式引入到电路系统中，方便各位工程师和从业人员更好地理解振动这种自然现象，并应用之。

第三部分：受迫振动

前面我们提到的简谐振动和阻尼振动，在振动过程中，除弹性力和阻尼力外，无其他维持振动的外力，这类振动被称为 自由振动 。

相对地，振动系统在连续周期性外力作用下发生的振动，我们称之为 受迫振动 。

在受迫振动中，假设周期性的外力为

此时的振动方程则被写成

这里，我们仅仅考虑弱阻尼的情况，同样可以得到方程的解析解

聪明的小伙伴，你们发现了没有，得到的微分方程 左边项的系数β是和系统自身性质相关 ，与外力无关；而方程右边项则是外力和激励频率ω决定。

下面我们针对解的物理意义做几点讨论（图中n为β）：

从上图中可以看出，当逐渐增大激励频率时，振幅大小会沿着振幅--圆频率曲线（ 幅频曲线 ）变动。当振幅达到极大值时，此时的频率被称为 共振频率 （或谐振频率）。不同的β对应不同的幅频曲线和共振频率。根据数学上求连续函数极值的方法，可以计算得到共振频率和共振时的振幅的解析值。

通过受迫振动的幅频曲线我们还可以知道， 振动系统具有选频特性。在共振频率点附近的周期激励产生的受迫振动振幅要明显大于远离共振频率处的周期激励所产生的。 假如一个系统的共振频率为10kHz，外部给的激励可以分解成800Hz,8kHz,80kHz三个余弦单位激励，那么最后系统所表现的谐振动（也即是系统的响应），一定是8kHz的最明显。

至此，我们则可以定性地理解上文中提到的Tacoma大桥的坍塌原因：风的频率接近桥梁受迫振动的共振频率，且此时的阻尼因子β较小，使得桥振动振幅不断增大，桥体形变产生的应力超过了桥的结构能承受的最大应力，从而桥体断裂。

以上就是振动现象的物理学基础。针对这一起手式，我们来划一下重点：

简谐振动是最基本的振动，它决定了振动的动力学特征是一个二阶微分方程。
有三种方法表示简谐振动，解析法，波形法，旋转矢量法。
自然界中的振动都是有阻尼的，阻尼振动的模型同样也可以简化成二阶微分方程；
阻尼振动，可以根据阻尼的大小划分成弱阻尼，过阻尼，临界阻尼三类形式，不同形式的阻尼振动波形不一样。
在周期性外力的激励下，阻尼振动可以升级成受迫振动。受迫振动是阻尼振动和谐振动的叠加。
受迫振动容易产生共振（谐振），共振条件即为激励频率等于系统共振频率。共振频率与系统自身的性质相关，与激励和初始条件无关。
振动系统具有选频特性。

二.双掌式

--时域与频域两个维度

前文中我们说到，要将振动的概念从一般的物理系统推广到电路系统中。在此之前，我们还需要处理 三个问题 ，第一个问题是， 采用什么样的方法或者算法解析受迫振动现象 。第二个问题，是如何 建立电路系统与起手式中振动系统的联系 。最后一个问题，则是如何描述电路系统，即通过何种模型，让电路的谐振运行状态更容易被量化。

1.对于第一个问题的答案，从起手式的讨论中我们可以初见端倪--既然受迫振动是和激励频率相关，那我们是否可以站得更高，将频率作为一个连续的自变量，单独讨论任何形状的周期性激励对系统的作用？

高等数学告诉我们，任何一个周期性连续函数都可以写成正余弦函数的无穷级数，即 傅里叶分解 。

这样，我们就可以将外力激励分解成无穷多个余弦激励，这无穷多个余弦激励对应不同的幅值（能量）和频率，并且其频率都是原始周期性激励频率的正整数倍。下图是以方波为例的傅里叶分解。

相应地，我们只需要单独求出系统对这无穷多个激励的响应，再将这些响应叠加，即可得到系统的总响应。（在这里我们再请大家思考，系统的总响应能由各个不同频率响应叠加的条件是什么？）

值得注意的是：我们在上文中提到了振动系统是具有选频特性的。 那么根据傅里叶分解得到的一系列余弦激励分量，并不是被均匀响应的。只有频率接近共振频率的那部分激励，仿佛是被系统选中了。这部分激励，才是对系统起决定性影响的外部激励。例如上图中基波频率为ν0的方波激励被分解成不同频率的余弦波激励，如果系统的共振频率为3ν0,那么系统就主要响应这部分频率为3ν0的余弦波激励，其他激励频率的分量被响应地相对更少。

至此，我们有了周期性激励对系统影响的描述方法，那么更进一步， 如果系统的激励是非周期性的呢？ 要回答这个问题，需要有信号与系统的基本理论基础--拉普拉斯变换。感兴趣的读者可以进一步去深入理解这部分内容，在这里我们不做过多的阐述，只讨论一种最特殊的情况，阶跃激励。

在振动系统中，我们经常会遇到阶跃输入的情况。例如，在机械振动系统中，突然加上一个100N的外力，再比如在电路系统中，调节直流输入电压，从30V突然调至60V，这里的“突然”，即是对应了激励源的一个上升沿，都可以认为是阶跃激励。

那么，如何量化阶跃激励呢？事实上，在信号与系统中，有对阶跃函数严格的数学定义。由于阶跃函数并非周期性连续函数，所以无法对其进行傅里叶分解。但是，如果我们只关心阶跃函数的上升沿，则可以认为阶跃函数是一个周期无穷大的方波（在工程领域，无穷大并不意味着数学上的高阶无穷大，只要这个周期远大于被研究对象的周期，我们可以认为这样的近似是合理的）。于是我们可以沿用方波的方式，继续做傅里叶分解。

例如上图中，F(x)为原始的单位阶跃激励（幅值为1），我们用一个周期为20，幅值为1，占空比为0.5的方波去模拟这个阶跃，对这个方波做傅里叶分解，图中F1(x),F2(x),F3(x)分别为保留了傅里叶级数前10项，前20项，前30项的逼近函数。

可以看到，保留的项数越多，逼近函数的上升沿斜率越大，越能模拟方波的上升沿。这意味着，阶跃激励的上升沿处包含了各个频率成分的激励分量。如果把阶跃激励施加于振动系统，由于振动系统的选频特性，振动系统必然会对某些频率的激励分量产生更明显的响应，这些频率即在振动系统的共振频率附近处。

以上，我们针对物理系统中的受迫振动系统，讨论了如何分析系统在不同激励下的响应。我们知道，在电工学中，有电压电流等物理量描述电路中各个元件运行的状态，并且实际电路中，这些物理量通常都是随时间变化的。接下来我们将把前文中的振动系统的状态量与电路中状态量进行对比，得到一致的振动形式。

2.我们对比二阶电路系统和前文中的二阶机械振动系统

上图中，左边为二阶电路系统，在t=0时刻，开关S闭合，输入电压激励vin(t)突然施加到电阻、电感及电容组成的串联电路两端。接下来，电路的运行满足基尔霍夫电压电流定律，欧姆定律，同时也要满足电感与电容充放电关系。

若把电容两端的电压vcr(t)当做响应，则整理上图中的方程可以得到

这个形式是不是似曾相识？

没错， 电容电压的运动方程仍然是二阶微分方程，与受迫机械振动具有相同的形式 。我们把上图中的方程化为首一形式：

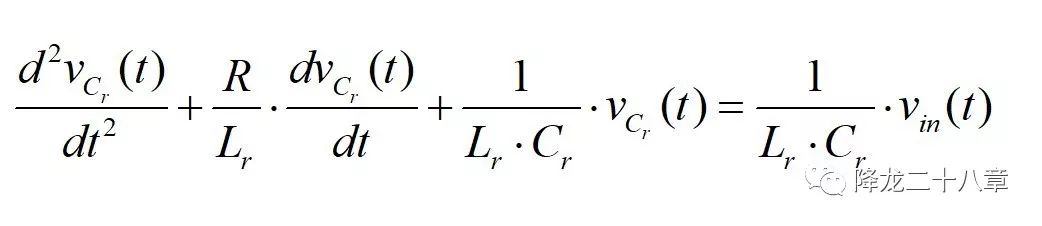
再对比受迫机械振动的方程：

两个方程形式上是非常统一的，更进一步，假设输入电源电压激励函数vin(t)为余弦函数，即vin(t)=Vin*cos(ωt)，我们可以列出两种系统中各个关键物理量的对比表：

由于二阶电路系统与机械振动系统的一致性，我们完全可以把起手式中的分析方法照搬到电路系统里面。

下面我们把阶跃输入电压作为电路激励，查看二阶电路系统对阶跃输入的响应。我们使用如下仿真电路，用幅值为200V，周期为2ms，占空比为0.5的方波脉冲电源去模拟阶跃激励。

上图中，橙色的波形为阶跃激励输入，蓝色的波形为电容的电压。可知在图中的这段时间内，系统在做阻尼振动。那么问题来了，阻尼振动的频率是多少呢？

我们前文中提到， 振动系统具有选频特性，而阶跃输入的上升沿处含有各个频率的激励分量。哪个频率的分量被选中了呢？没错，就是共振频率 。

图中给出的频率35.7kHz，也可以通过计算得到。考虑到电路的阻尼电阻0.4欧姆（0.3欧姆电阻加电感寄生0.1欧姆），电感量80uH,电容量240nF,计算得到阻尼因子β为2.5e3,圆频率ω0为2.28e5rad/s,共振频率ωr=2.27e5,转化成实际频率fr=36.3kHz，与波形中的测量的频率非常接近了。

再让我们回顾上文提到的解决步骤：第一步先将激励进行傅里叶分解，得到余弦函数无穷级数，第二步根据每个单独的余弦函数的幅值和频率，根据系统的幅频曲线或者微分方程特解得到对应的响应。第三步将无穷多个（在误差允许的范围内可以只计算有限个）响应矢量叠加，得到总响应。

但这样的方法存在一个严重的问题：

这三步每一步的原理都非常清晰，但如果振动系统稍微复杂，激励形式更加多样化，在实际运算中就会涉及到大量的微分方程，傅里叶分解及矢量合成，计算量较大，在工程上的可行性不高。所以我们接下来会引入复频域的概念，也同时来回答第三个问题。

3.前文对振动模型的分析都是在时域，并且指出了时域分析运算的复杂性，可见时域电路模型不适合应用在阶数较高（二阶及更高阶）的振动系统。在这里我们还是采用之前提到的拉普拉斯变换的思想（哈哈，逃不掉的），将电路的微分运动方程，用复频域的代数方程替代，更便捷地描述电路中电压电流关系，最后再利用拉普拉斯反变换，得到电压电流响应的时域方程。

关于拉普拉斯变换在电路应用中的合理性，在数学上是能够严格证明的，详情可参考 信号与系统 。这里我们同样只考虑频域的电路谐振模型，不对拉氏变换做太多的解释。

根据拉氏变换，时域电路模型与频域电路模型的等价如下：

A）对于电阻模型

B）对于电感模型

C）对于电容模型

其中iL(0-)和uc(0-)分别是开关闭合前的电感电流和电容电压。

这样，我们的二阶电路系统的频域运算模型就已经建立，如下图

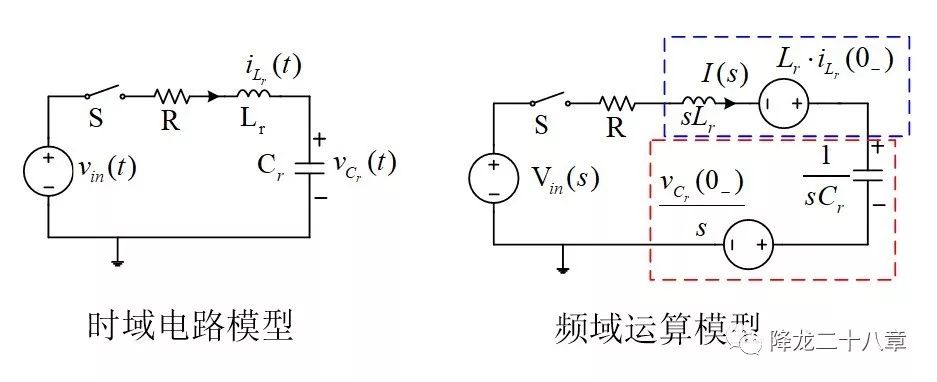
假设初始状态电感和电容两个元件上都无储能，即iL(0-)和uc(0-)均为零，则可以写出频域中电容电压Vcr(s)和输入电压Vin(s)的关系式:

得到这样的传递关系后，电路的响应求取就明确了。步骤如下：

第一步：将时域上的激励输入函数vin(t)做拉氏变换，得到频域的Vin(s)，

第二步：根据上述关系式得到电容电压的频域表达式Vcr(s)，

第三步：对Vcr(s)做拉氏反变换，得到时域的响应函数vcr(t)。

下面我们同样以200V的阶跃输入作为激励，求取电容电压函数。 单位阶跃函数ε(t)的拉普拉斯变换为1/s ,带入到上图中的表达式，并考虑弱阻尼的情况：

上图中表达式即为单位阶跃激励下的电容电压的频域表达式，为了方便做拉普拉斯反变换，将其整理成等号右边的形式（中括号内第一项对应时域的指数函数，第二项对应时域上衰减的余弦函数，第三项对应时域上衰减得正弦函数），使用待定系数法可以求得A，B，C，最后即可得到时域电容电压函数vcr(t)及波形。

把上文的电路参数带入到电容时域电压表达式，可以得到波形如下：

由图可见，该波形与上文中时域分析仿真得到的波形一致，也证明了频域运算模型的有效性。

以上，我们分别从时域和频域分析了二阶振动电路的性质，阐述了时域与频域之间的联系，时域模型和频域模型本质上是等价的，是看待同一事物的不同角度。但当电路系统中电感和电容数量较多，电路的阶数较高时，显然频域模型更加实用。

双掌式要义总结：

二阶电路系统与二阶机械振动系统形式统一，所有用于研究机械系统振动的方法都可以搬用到二阶电路系统。
时域上求解二阶电路系统的方法：先列写系统微分方程，再对输入激励做傅里叶分解，把每个频率的激励分量施加到微分方程的激励函数，得到相应的特解。将各个特解矢量叠加。
频域上求解二阶及高阶电路系统的方法：先将电路时域模型转化成频域模型，得到频域传递函数，再将激励函数做拉氏变换后与传递函数相乘，得到响应的频域表达式，最后拉氏反变换得到时域响应。
频域方法比时域方法更适合二阶以上的电路系统。

三.出掌风

--电力电子电路中的谐振应用例

前两部分我们分别探讨了机械振动系统和电路系统中谐振现象的物理基础及其分析与求解方法，接下来我们便要将上文中的理论用于实际的电路中。（本部分供电力电子相关专业人员参考）

在电力电子电路中，谐振现象广泛存在。有的电路需要避免谐振，例如反激电路需要减小漏感与开关管寄生电容的谐振以减小开关管电压应力；有的电路则是利用谐振实现软开关，如LLC谐振电路。 我们在本篇中重点介绍利用谐振实现软开关的一个例子--单管并联谐振电路 。

这个电路被应用到我们常用的家居生活电器电磁炉中。

我们知道，高频的交流磁场在铁磁材料中可以产生涡流，使得铁磁材料被加热，电磁炉正是利用了这个原理。下图为电磁炉中单管谐振电路的拓扑图

图中，Req和Leq分别为放上锅体后等效到电路中的电阻和电感，Q1和D1分别为IGBT开关管和续流二极管，Vin为交流输入电压整流后的馒头波电压，这里我们只考虑稳态运行时馒头波电压峰值处的情况。

稳态时的一个开关周期内，这个电路存在四个关键模态，如下图

这里，IGBT关断后的模态2和模态3，是电感与电容的谐振过程，是一个典型的阻尼振动。我们有两种方法来描述这个谐振过程，时域和频域。这里我们不做过多的推导及计算，我们直接给出模态2和模态3两个过程中IGBT的集射电压Vce的表达式：

从表达式中可以看到Vce电压不仅和输入电压相关，还和关断前的IGBT电流峰值Ipk相关，这也对应了频域模型中的电感初始储能。

为了能实现ZVS，Vce电压必须到零，续流二极管才会导通 。如果Vce电压谐振回不到零，则不具备ZVS条件，此时如果开通IGBT，谐振电容电压瞬间被充电至Vin，从Vce波形上此处仿佛有个台阶打破了正常的谐振，产生较大的脉冲电流，被损耗到IGBT的沟道中，使得IGBT结温被抬高，可能超出安全工作区。