光栅色散介绍

衍射光栅的主要目的是按波长在空间上散射光。入射到光栅上的白光束在从光栅衍射时将被分离为其分量波长，每个波长沿着不同的方向衍射。色散是测量不同波长衍射光之间的分离(角度或空间)。角色散表示每单位角度的光谱范围，线性分辨率表示每单位长度的光谱范围。

角色散

波长λ和λ+Δλ之间的m阶光谱的角扩展Δβ可以通过微分光栅方程获得，假设入射角α为常数。因此，每单位波长衍射角的变化D为：

D = dβ/dλ = m / dcosβ = (m/d)secβ = Gm secβ (2-13)

其中β为衍射角，量D称为角色散。随着凹槽频率G=1/d的增加，角色散增加(意味着波长之间的角分离随阶数m增加)。

在等式(2-13)中，重要的是要认识到，量m/d不是可以独立于其他参数比率;将光栅方程代入方程(2-13)得到以下角色散的一般方程：

D = dβ/dλ = (sinα + sinβ) / λcosβ (2-14)

对于给定的波长，这表明角色散可以被认为仅仅是入射角和衍射角的函数。当我们考虑Littrow配置(α=β)时，这一点变得更加清楚，在这种情况下，方程(2-14)简化为：

D = dβ/dλ = (2/λ) tanβ, in Littrow. (2-15)

在Littrow使用中，当|β|从10°增加到63°时，可以从方程(2-15)中看出角色散增加了10倍，而与所考虑的光谱阶数或波长无关。一旦确定了衍射角β，就必须选择是以低衍射级使用细间距光栅(小d)，还是以高衍射级使用粗间距光栅(大d)，如阶梯光栅。[然而，细间距光栅将提供更大的自由光谱范围;]

线色散

对于给定的m阶衍射波长λ(对应于衍射角β)，光栅系统的线色散是角色散D和系统有效焦距r'(β)的乘积：

r'D = r'(dβ/dλ) = mr'/dcosβ = (mr'/d)secβ = Gmr'secβ (2-16)

量r'Δβ=Δl是沿着光谱的位置变化(实际距离，而不是波长)。定义焦距r'(β)，以明确地表明它可能取决于衍射角β(而衍射角β又取决于λ)。

倒数线色散P，更常被考虑;它只是r’D的倒数:

P = dcosβ / mr' (2-17)

通常以nm/mm测量(其中d以nm表示，r’以mm表示)。量P是波长(以nm为单位)的变化的量度，该波长(以mm为单位)对应于沿着光谱的位置的变化。[需要注意的是，一些作者使用P来表示1/sinΦ的量，其中Φ是光谱与垂直于衍射射线的线所成的角度(见图2-6);为了避免混淆，我们将1/sinφ的量称为倾斜因子。]当特定波长的像平面不垂直于衍射射线时(即，当Φ≠90°时)，必须将P乘以倾斜因子，以获得像平面中正确的倒数线性色散。

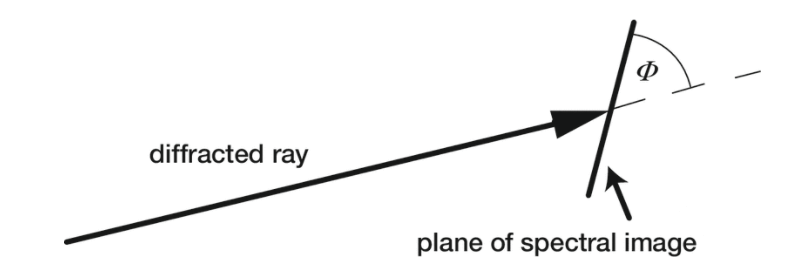
图2-6 记录的光谱图像不需要位于垂直于衍射射线的平面内(即Φ≠90°)

审核编辑 黄宇