ICLR 2024高分投稿：用于一般时间序列分析的现代纯卷积结构

这篇是 ICLR 上用 TCN 来做一般的时间序列分析的论文，在 Rebuttal 之后的分数为 888，算得上是时间序列领域相关的论文中最高分那一档了。本文提出了一个 ModernTCN 的模型，实现起来也很简单，所以我后面附上了模型的代码实现。

论文标题：

ModernTCN: A Modern Pure Convolution Structure for General Time Series Analysis

论文链接：

https://openreview.net/forum?id=vpJMJerXHU

Key Point

1.1 Motivation

作者发现，在时间序列领域，最近基于 TCN/CNN 的模型效果没有基于Transformer 或 MLP 的模型效果好，而一些现代的 CNN 比如 ConvNeXt、SLaK 的性能都超过了 Vision Transformer。因此，作者想探究卷积是不是可以在时间序列分析领域获得更好的性能。为此，有两点可以改善 TCN 模型的地方。

首先是要提升感受野。在 CV 领域，现代卷积都有着很大的卷积核。作者发现在时间序列领域差不多，可以看下图：

SCINet 和 MICN 是两个基于 TCN 的预测模型，它们的感受野都很小。作者发现 ModernTCN 中采用大的卷积核所对应的感受野要大很多。

其次是充分利用卷积可以捕获跨变量依赖性，也就是多变量时间序列中变量之间的关系。在 PatchTST 等最近的时间序列预测文章中，很多方法采用了通道独立策略，这种策略直接将多变量序列预测中变量之间关系忽略了，反而取得了更好的效果。作者认为，变量之间关系仍然重要，但是要精心设计模型结构来捕获。

1.2 从CV中汲取灵感（现代卷积结构）

在 CV 中，很多人发现 Transformer 之所以成功，可能是因为架构比较好。比如下图左侧，self-attention 负责 token 之间的混合，FFN 负责通道之间的混合，两者分离开。同样的，把混合 token 的结构替换为深度分离卷积（depth-wise 卷积，DWConv），把 FFN 换为完全等价的 ConvFFN（由两个 point-wise Conv 加 GeLU 激活组成）。

不熟悉 depth-wise 卷积的可以去了解一下，它其实就是对每个通道采用独立的核，这样就不会混合通道，只会混合 token，大卷积核来获取大感受野也是在这里用的。

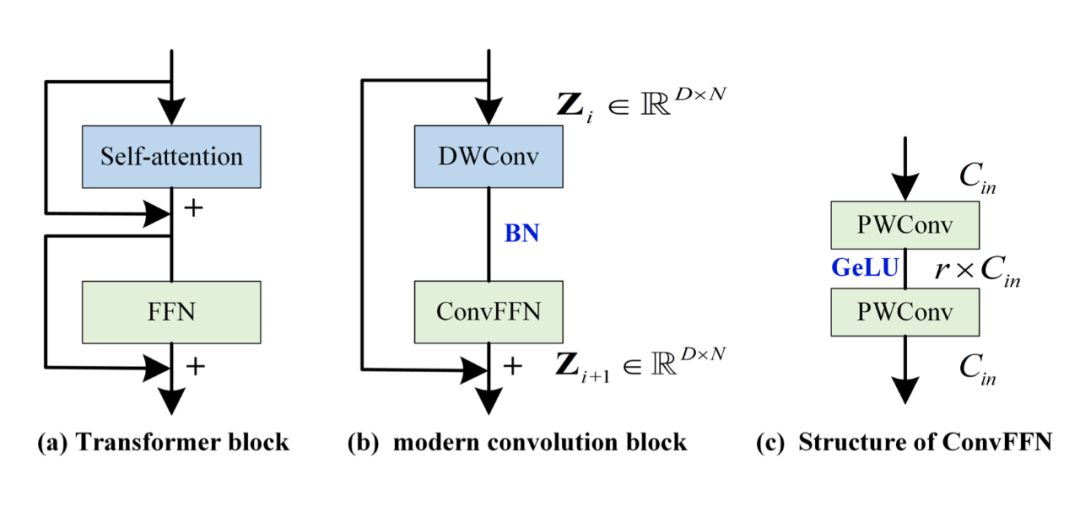
然而，作者发现采用上图（b）的结构构建的模型效果也不是特别好，这是因为这个现代卷积结构中并没有专门为时间序列设计的一些特殊的东西，一个重要的就是如何建模跨变量依赖性。注意，在这里要区分通道和变量之间的关系。变量是指多变量序列中每个变量，通道是指每个变量映射到的隐空间维度（而 PatchTST 中提到的通道独立则是变量之间独立，这个不要混淆）。ConvFFN 可以建模通道间关系，但无法建模变量间关系。

1.3 适用于时间序列的改动（变量间建模）

首先，在 embedding 的过程中，cv 一般是直接混合 RGB 变量。而在时间序列中，这种方式不适用，因为一个简单的 embedding 显然无法充分建模变量间关系。如果在 embedding 时就已经把变量混合了起来，那后续对变量间的建模则是混乱的。

因此，作者提出了变量无关 embedding，也是用了分 patch 的方法，对每个变量独立分 patch 进行 embedding。具体在代码实现上，作者是采用有 stride 的卷积，在这里我给出了代码实现，先介绍下代码相关的注释：

# B：batch size
# M：多变量序列的变量数
# L：过去序列的长度
#T:预测序列的长度
#N:分Patch后Patch的个数
# D：每个变量的通道数
# P：kernel size of embedding layer
# S：stride of embedding layer

Embedding 模块先将 的输入 unsqueeze，新增一个通道维，然后 pad 之后（方便整除）应用有 stride 的 1D 卷积来进行 patch embedding，如下：

classEmbedding(nn.Module):
def__init__(self,P=8,S=4,D=2048):
super(Embedding,self).__init__()
self.P=P
self.S=S
self.conv=nn.Conv1d(
in_channels=1,
out_channels=D,
kernel_size=P,
stride=S
)

defforward(self,x):
#x:[B,M,L]
B=x.shape[0]
x=x.unsqueeze(2)#[B,M,L]->[B,M,1,L]
x=rearrange(x,'bmrl->(bm)rl')#[B,M,1,L]->[B*M,1,L]
x_pad=F.pad(
x,
pad=(0,self.P-self.S),
mode='replicate'
)#[B*M,1,L]->[B*M,1,L+P-S]

x_emb=self.conv(x_pad)#[B*M,1,L+P-S]->[B*M,D,N]
x_emb=rearrange(x_emb,'(bm)dn->bmdn',b=B)#[B*M,D,N]->[B,M,D,N]

returnx_emb#x_emb:[B,M,D,N]

在 Embedding 之后，作者用一些堆叠的 Block 来进行建模。每个 Block 如下图：

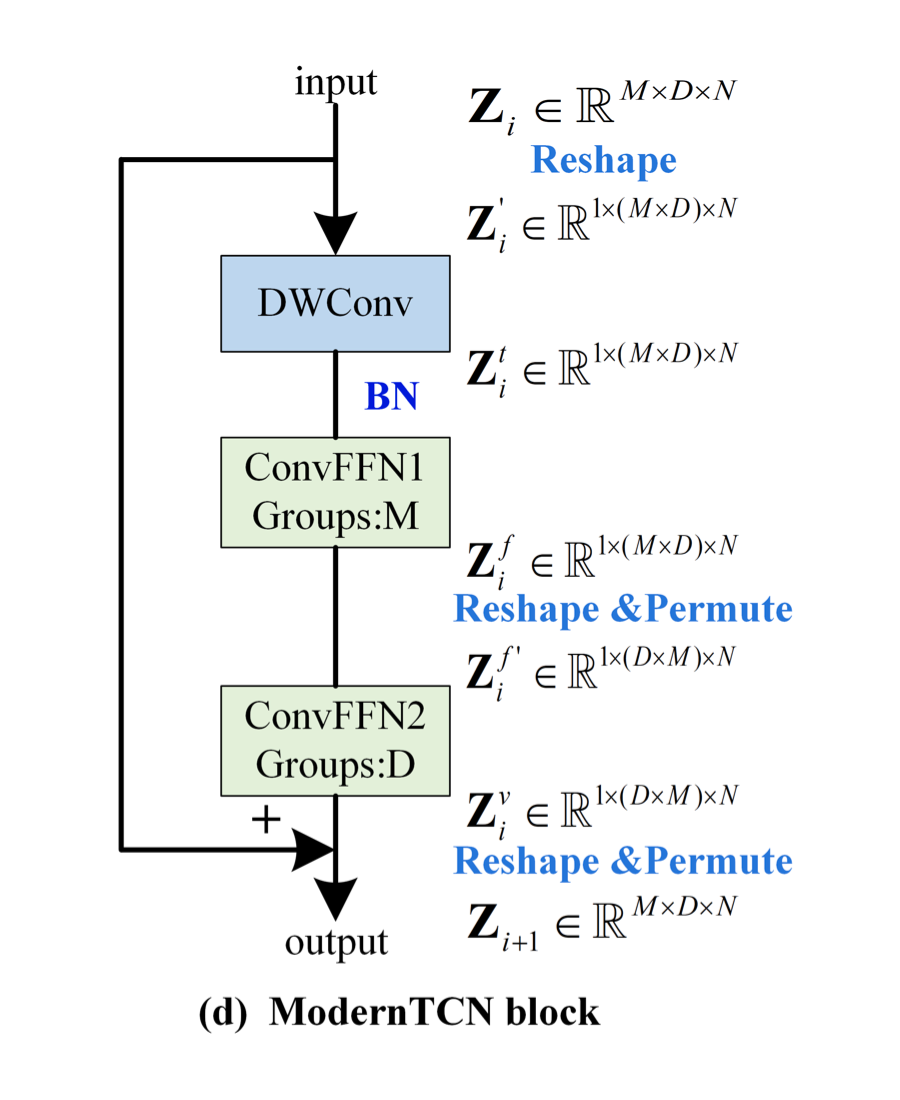
上图中 DWconv 用来建模时间关系，第一个 ConvFFN 用来建模通道关系，第二个 ConvFFN 用来建模变量关系。下面介绍具体的实现，注意看上图中 shape 在每一个模块的前后变化。

首先，希望用 DWConv 来建模时间上的关系，但又不希望它参与到通道间和变量间的建模上。因此，作者将 M 和 D 这两个表示变量和通道的维度 reshape 在一起，再进行深度可分离卷积。

其次，希望独立建模通道和变量。因此，作者采用了两个组卷积，其中一个组卷积的 Group 数为 M（表示每 D 个通道构成一个组，因此用来建模通道间关系），另一个组卷积的 Group 数为 D（表示每 M 个变量构成一个组，因此用来建模变量间关系）。注意，两个组卷积之间存在着 reshape 和 permute 操作，这是为了正确的分组，最后会再 reshape 和 permute 回去。

最后，整体再用一个残差连接，即可得到最终的 ModernTCN block。ModernTCN block 的代码实现在最后，堆叠多个 block 即可得到 ModernTCN 模型。

综上所述，作者将时间上、通道上、变量上的三种关系解耦建模，用三种组卷积来巧妙地进行实现（深度可分离卷积其实也是组数等于深度数的组卷积），既简单又有效。

实验

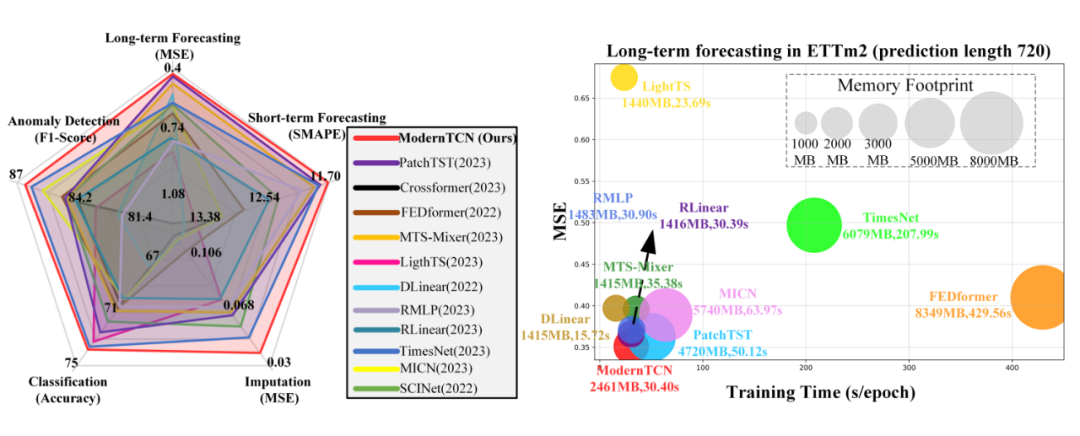
作者也是在各种时间序列任务上进行了实验，如下图，又快又好的五边形战士：

代码实现

注意，我这里实现的模型是用于时间序列预测任务的，在 backbone 的基础上加了个预测头，具体的结构在论文附录图 5。

importtorch
importtorch.nnasnn
importtorch.nn.functionalasF
fromeinopsimportrearrange

# B：batch size
# M：多变量序列的变量数
# L：过去序列的长度
#T:预测序列的长度
#N:分Patch后Patch的个数
# D：每个变量的通道数
# P：kernel size of embedding layer
# S：stride of embedding layer

classEmbedding(nn.Module):
def__init__(self,P=8,S=4,D=2048):
super(Embedding,self).__init__()
self.P=P
self.S=S
self.conv=nn.Conv1d(
in_channels=1,
out_channels=D,
kernel_size=P,
stride=S
)

defforward(self,x):
#x:[B,M,L]
B=x.shape[0]
x=x.unsqueeze(2)#[B,M,L]->[B,M,1,L]
x=rearrange(x,'bmrl->(bm)rl')#[B,M,1,L]->[B*M,1,L]
x_pad=F.pad(
x,
pad=(0,self.P-self.S),
mode='replicate'
)#[B*M,1,L]->[B*M,1,L+P-S]

x_emb=self.conv(x_pad)#[B*M,1,L+P-S]->[B*M,D,N]
x_emb=rearrange(x_emb,'(bm)dn->bmdn',b=B)#[B*M,D,N]->[B,M,D,N]

returnx_emb#x_emb:[B,M,D,N]


classConvFFN(nn.Module):
def__init__(self,M,D,r,one=True):#oneisTrue:ConvFFN1,oneisFalse:ConvFFN2
super(ConvFFN,self).__init__()
groups_num=MifoneelseD
self.pw_con1=nn.Conv1d(
in_channels=M*D,
out_channels=r*M*D,
kernel_size=1,
groups=groups_num
)
self.pw_con2=nn.Conv1d(
in_channels=r*M*D,
out_channels=M*D,
kernel_size=1,
groups=groups_num
)

defforward(self,x):
#x:[B,M*D,N]
x=self.pw_con2(F.gelu(self.pw_con1(x)))
returnx#x:[B,M*D,N]


classModernTCNBlock(nn.Module):
def__init__(self,M,D,kernel_size,r):
super(ModernTCNBlock,self).__init__()
#深度分离卷积负责捕获时域关系
self.dw_conv=nn.Conv1d(
in_channels=M*D,
out_channels=M*D,
kernel_size=kernel_size,
groups=M*D,
padding='same'
)
self.bn=nn.BatchNorm1d(M*D)
self.conv_ffn1=ConvFFN(M,D,r,one=True)
self.conv_ffn2=ConvFFN(M,D,r,one=False)

defforward(self,x_emb):
#x_emb:[B,M,D,N]
D=x_emb.shape[-2]
x=rearrange(x_emb,'bmdn->b(md)n')#[B,M,D,N]->[B,M*D,N]
x=self.dw_conv(x)#[B,M*D,N]->[B,M*D,N]
x=self.bn(x)#[B,M*D,N]->[B,M*D,N]
x=self.conv_ffn1(x)#[B,M*D,N]->[B,M*D,N]

x=rearrange(x,'b(md)n->bmdn',d=D)#[B,M*D,N]->[B,M,D,N]
x=x.permute(0,2,1,3)#[B,M,D,N]->[B,D,M,N]
x=rearrange(x,'bdmn->b(dm)n')#[B,D,M,N]->[B,D*M,N]

x=self.conv_ffn2(x)#[B,D*M,N]->[B,D*M,N]

x=rearrange(x,'b(dm)n->bdmn',d=D)#[B,D*M,N]->[B,D,M,N]
x=x.permute(0,2,1,3)#[B,D,M,N]->[B,M,D,N]

out=x+x_emb

returnout#out:[B,M,D,N]


classModernTCN(nn.Module):
def__init__(self,M,L,T,D=2048,P=8,S=4,kernel_size=51,r=1,num_layers=2):
super(ModernTCN,self).__init__()
#深度分离卷积负责捕获时域关系
self.num_layers=num_layers
N=L//S
self.embed_layer=Embedding(P,S,D)
self.backbone=nn.ModuleList([ModernTCNBlock(M,D,kernel_size,r)for_inrange(num_layers)])
self.head=nn.Linear(D*N,T)

defforward(self,x):
#x:[B,M,L]
x_emb=self.embed_layer(x)#[B,M,L]->[B,M,D,N]

foriinrange(self.num_layers):
x_emb=self.backbone[i](x_emb)#[B,M,D,N]->[B,M,D,N]

#Flatten
z=rearrange(x_emb,'bmdn->bm(dn)')#[B,M,D,N]->[B,M,D*N]
pred=self.head(z)#[B,M,D*N]->[B,M,T]

returnpred#out:[B,M,T]


past_series=torch.rand(2,4,96)
model=ModernTCN(4,96,192)
pred_series=model(past_series)
print(pred_series.shape)
#torch.Size([2,4,192])

Comments

附录很长，里面的消融实验很充分，效果也很好，想法很合理，实现起来也很简单，估计能中 oral。不过感觉在那几个时间序列预测任务上的数据集都快刷爆了，性能快到瓶颈了，感觉之后很难再有大的效果提升了。

---

原文标题：ICLR 2024高分投稿：用于一般时间序列分析的现代纯卷积结构

文章出处：【微信公众号：智能感知与物联网技术研究所】欢迎添加关注！文章转载请注明出处。